Algoritmusok - Spurs (végleges)
20'Printsipy profil majdnem üres hálózat mátrixok Gauss elimináció.
1) A megszüntetése nem nulla elemek a Gauss módszer kell lenni, hogy közben a kivételek meg minimális számú új nullától elemek;
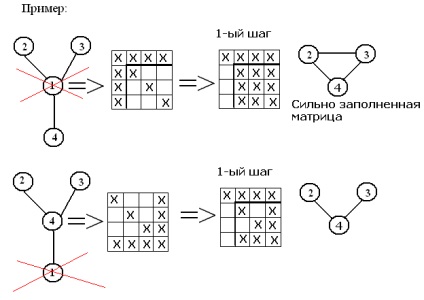
Összesen: 1) Szükséges vagy megváltoztatni a kezdő érdekében a csomópontok
2) Alternatív módon, anélkül, hogy megváltoztatná a sorrendben a kivétel átnevezés egységek (lásd jegyet 23)
kivétel: az első helyen kell zárni csomópontok kevésbé gyakran más csomópontok (amelyek a legkisebb számú eset linkek más elemekkel)
2) A memóriában tárolt kell csak zérus elemet csak egyszer kell előállítani őket aritmetikai műveletek (lásd a jegy 24)
21'Poryadok megszüntetése ismeretlenek a Gauss módszer fordított hinta.
1) A megszüntetése nem nulla elemek a Gauss módszer kell lenni, hogy közben a kivételek meg minimális számú új nullától elemek;
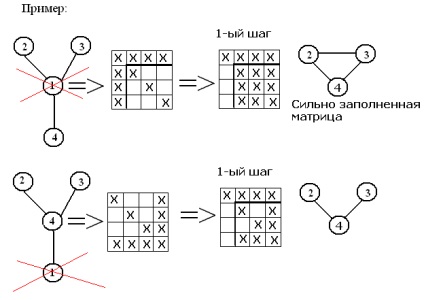
Összesen: 1) Szükséges vagy megváltoztatni a kezdő érdekében a csomópontok
2) Alternatív módon, anélkül, hogy megváltoztatná a sorrendben a kivétel átnevezés egységek (lásd jegyet 23)
kivétel: az első helyen kell zárni csomópontok kevésbé gyakran más csomópontok (amelyek a legkisebb számú eset linkek más elemekkel)
2) A memóriában tárolt kell csak zérus elemet csak egyszer kell előállítani őket aritmetikai műveletek (lásd a jegy 24)
22 „jelentése a kitöltési tényező mátrixok. Tárolása nem nulla a mátrix elemei.
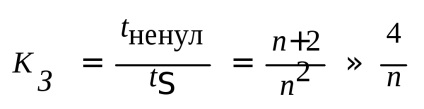
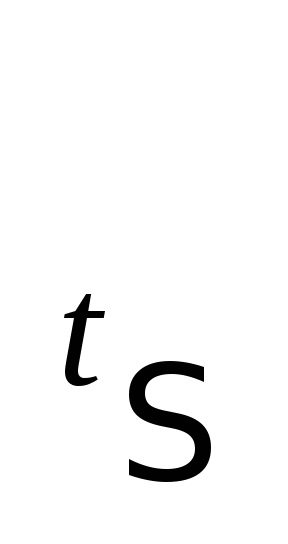
A nagy rendszer
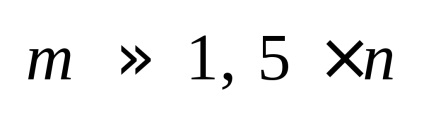
Következtetés: a minél több áramköri elemek a kisebb együtthatót teljessége
Ez csak akkor szükséges, hogy tárolja a nem zéró mátrix elemeinek Y, ahol csak a felső Δ, mivel a mátrix Y - szimmetrikus
mátrix tárolási követelmények rendszereket.
2) Könnyű képező
3) Egyszerű használat
a) egyszerűség minták
b) változó a tárolt információt rugalmasság
(Mivel a mező 1 lépés pojavl. Új nem nulla elemek)
I. definiálása az egyetlen nem nulla. elemek:
23 „algoritmusok a megrendelés, azok besorolását.
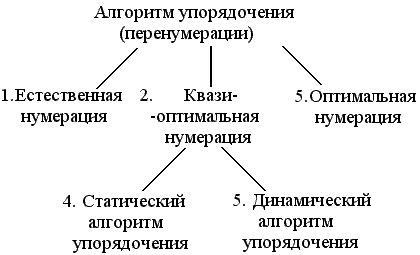
2) kompromisszum a szoftver nem túl bonyolult, és a készülék memóriájában átszámozásával megtakarítás
3) a rendelési folyamat zajlik előtt kizárásával csomópontok
4) végeztünk mindenegyes előre menetben lépés
5) számozás, ami arra utal, min. igényelt memória mennyisége min. A teljes száma nem nulla elemek
Amikor a program átszámozására fordul egyetlen kivétel folyamat szimuláció ismeretlen
24 „tárolása ritka mátrixok. mátrixok csomagolás rendszer. mátrix tárolási követelmények rendszereket.
2) Könnyű képező
3) Egyszerű használat
a) egyszerűség minták
b) változó a tárolt információt rugalmasság
(Mivel a mező 1 lépés pojavl. Új nem nulla elemek)
I. definiálása az egyetlen nem nulla. elemek:
Hoz létre a további tömb NADR - számértéket cellaelrendezés ahonnan vezetőképesség kezdődik társított csomóponthoz
7-6, mivel az e-nek csak ÉRTÉK, azt mutatja, hogy több, mint bármi más nincs csatlakoztatva.
26 „és algoritmikus szoftver megvalósítása matritsyYv képező kompakt formában .Sm.25 program:
Szubrutin YSZ (nn, nk, Z, YC, y, diag, nzero, értéket, icol, nadr, n, m)
Komplex z (m), YC (m), diag (n), (1) értéket
Dimension nzero (n), icol (1), nadr (n)
ha (i1 * i2.ne.0), akkor j = i2
nadr (i) = nadr (i-1) + nzero (i-1)
ha (i1 * i2.ne.0), akkor j = i2
end do szélső
27 „Iteratív ur számítás. SD számítási algoritmus Seidel módszerrel.
1) a gördülő módszerek - m ahol a változók keresett a kimenő hívás az egyes pályán .. UR-I sorozat.
2) egyidejűleg. december ur. - minden ur. december rendszer Xia egyidejűleg minden iteráció.
Bal.tokov: Gauss módszer, kezelésére, mátrix faktorizáció
Ball. Kapacitás: Newton-módszer
1) a számítások mennyiségét minden. iteráció;
2) a teljes száma iterációk;
3) a teljes számítási időt.
Egyáltalán hatékony és abszolút konvergens módszerek
28 „Seidel módszert alkalmazzák, hogy a megoldás a nemlineáris csomóponti ur-I formájában egyensúlyt áramok.