A vizuálisan érdekes!
Grafy.Chto ez, és miért van szükség?
Miután a nagy matematikus Leonhard Euler megkérdezték: Van-e lehetőség, hogy megkerülje a hét hidat állva majd Königsberg (ma Kalinyingrád, Oroszország), miután minden egyszerre? Mielőtt Königsberg terv -, akkor próbáld ki!
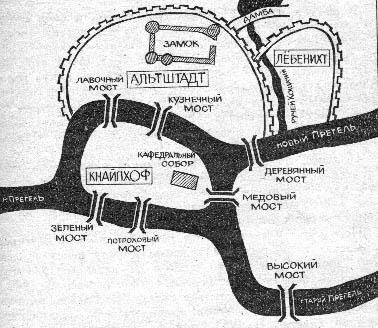
Úgy véljük, ez a probléma, 1736-Euler bebizonyította, hogy ez nem lehetséges, és úgy ítélték az általánosabb probléma: milyen területen elválasztott Bayous és hidak kötik össze, ez lehetséges-hoz kap körül, látogatás minden híd pontosan egyszer, és mi lehetetlen.
Némileg módosítani a feladatot. Mind a fent említett területeken folyó választja el egymástól, jelölt pontok, valamint a hidak összekötő őket - a szegmens a vonal (nem feltétlenül egyenes). Ezután ahelyett, hogy a terv működni fog csak egy bizonyos értéknél, tagjai szegmensei görbék és egyenesek. Ezek a számok a modern matematika nevű grafikon, a szegmensek - a bordák, és a pontokat, hogy összekössék a bordákat - maximum. Ezután az eredeti probléma egyenértékű a következő: lehetséges, hogy felhívja a grafikon felemelése nélkül ceruzát a papírról, hogy van, úgy, hogy minden él csak egyszer haladnak. Ilyen grafikonokat lehet levonni felemelése nélkül ceruzát a papírról, az úgynevezett unicursal (a latin unus cursus - egy út) vagy Euler. Így a probléma megfogalmazása tehát: milyen körülmények között Earl unikursalen? Nyilvánvaló, unicursal grafikon nem szűnik meg unicursal, ha megváltoztatja a hosszát vagy alakja bordáját, és változtassa meg a vertex helyen -, de nem változtatna kapcsolatot felsők bordák (abban az értelemben, hogy ha két pont között, akkor kell csatlakoztatni, és ha megszakad - nincs csatlakoztatva).
Ha a gráf unikursalen, majd topológiai egyenértékű grafikon is unicursal. Unicursal tehát egy topológiai tulajdonsága a grafikonon.
Először is, meg kell különböztetni a csatlakoztatott grafikonok megszakad. Összetartó nevezett számok úgy, hogy bármely két pont össze lehet bármilyen eszközzel, ahhoz tartozó szám. Például a legtöbb betű az orosz ábécé vannak kötve, de az N betű - No: lehetetlen, hogy menjen a bal fele a jobb, a pontok tartozó ezt a levelet. Connectivity - topológiai tulajdonság: nem változik meg átalakulások számok szakadás nélkül, és ragasztással. Nyilvánvaló, hogy ha a gráf unikursalen meg kell csatlakoztatni.
Másodszor, nézd meg a tetején a grafikonon. Fel fogjuk hívni a felső index élek számát találhatók ebben a tetején. Most kérdezzük meg magunktól: mi lehet egyenlő az indexek csúcsok unicursal grafikonon.
Lehet kezdődik és ér véget ugyanazon a ponton (nevezzük „zárt pályán”) vonalat húzunk grafikon, és lehet a különböző (nevezzük „nem zárt pályán”): Lehet, hogy két esetben. Próbálja ki Ön is, hogy dolgozzon egy ilyen vonal -, hogy mit szeretne önálló csomópontok - .. dupla, tripla, stb (az érthetőség kedvéért, a legjobb, ha a bordák nem volt több, mint 15).
Könnyen belátható, hogy egy zárt módon minden csúcsának még indexek, és nyitott - pontosan két páratlan (ez a kezdet és a vég, az út). A tény az, hogy ha a csomópont nem a kezdet és vége, jött rá, mi kell majd belőle - így hány élek szerepelnek benne, mint sok belőle, de csak annyi bejövő és kimenő élek még . Ha a kezdeti csúcs egybeesik a végén, ez is egy index akár hány széleit úgy jött ki, és ugyanazt a számot beírni. És ha a kiindulási pont nem esik egybe a vég, a páratlan indexek: a kiindulási pontot kell egyszer kijutni, majd ha visszatér, majd hagyjuk újra, ha vissza -, hogy hagyja megint, stb.,. és a végén el kell jönnie, és ha ki belőle, majd kimegy, akkor meg kell, hogy menjen vissza, és így tovább. d.
Ahhoz, hogy a gróf unicursal, az szükséges, hogy minden csúcsának még indexek, illetve a csúcsok száma páratlan index megegyezik a kettő.
Most nézd meg megint a grafikont a probléma Königsberg híd.
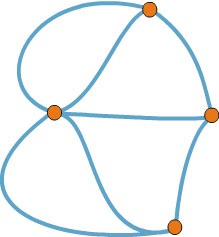
Számolja az indexek a csúcsok és győződjön meg róla, hogy nem lehet unicursal. Ezért nem kap, ha azt szeretné, hogy megkerülje az összes hidat.