A probléma a königsbergi hidak 1
Ábra. 3. Gróf Königsberg híd
Némileg módosítani a feladatot. Mind a fent említett területeken folyó választja el egymástól, jelölt pontok, valamint a hidak összekötő őket - a szegmens a vonal (nem feltétlenül egyenes). Ezután ahelyett, hogy a terv működni fog csak egy bizonyos értéknél, tagjai szegmensei görbék és egyenesek. Ezek a számok a modern matematika nevű grafikon, a szegmensek - a bordák, és a pontokat, hogy összekössék a bordákat - maximum. Ezután az eredeti probléma egyenértékű a következő: lehetséges, hogy felhívja a grafikon felemelése nélkül ceruzát a papírról, hogy van, úgy, hogy minden él csak egyszer haladnak.
Ilyen grafikonokat lehet levonni felemelése nélkül ceruzát a papírról, az úgynevezett unicursal (a latin unus cursus - egy út) vagy Euler. Így a probléma megfogalmazása tehát: milyen körülmények között Earl unikursalen? Nyilvánvaló, unicursal grafikon nem szűnik meg unicursal, ha megváltoztatja a hosszát vagy alakja bordáját, és változtassa meg a vertex helyen -, de nem változtatna kapcsolatot felsők bordák (abban az értelemben, hogy ha két pont között, akkor kell csatlakoztatni, és ha megszakad - nincs csatlakoztatva).
Ábra. 4. topológiailag egyenértékű grafikonok
Ha a gráf unikursalen, majd topológiai egyenértékű grafikon is unicursal. Unicursal tehát egy topológiai tulajdonsága a grafikonon.
Először is, meg kell különböztetni a csatlakoztatott grafikonok megszakad. Összetartó nevezett számok úgy, hogy bármely két pont össze lehet bármilyen eszközzel, ahhoz tartozó szám. Például a legtöbb betű az orosz ábécé vannak kötve, de az N betű - No: lehetetlen, hogy menjen a bal fele a jobb, a pontok tartozó ezt a levelet. Connectivity - topológiai tulajdonság: nem változik meg átalakulások számok szakadás nélkül, és ragasztással. Nyilvánvaló, hogy ha a gráf unikursalen meg kell csatlakoztatni.
Másodszor, nézd meg a tetején a grafikonon. Fel fogjuk hívni a felső index élek számát találhatók ebben a tetején. Most kérdezzük meg magunktól: mi lehet egyenlő az indexek csúcsok unicursal grafikonon.
Lehet kezdődik és ér véget ugyanazon a ponton (nevezzük „zárt pályán”) vonalat húzunk grafikon, és lehet a különböző (nevezzük „nem zárt pályán”): Lehet, hogy két esetben. Próbálja ki Ön is, hogy dolgozzon egy ilyen vonal -, hogy mit szeretne önálló csomópontok - .. dupla, tripla, stb (az érthetőség kedvéért, a legjobb, ha a bordák nem volt több, mint 15).
Könnyen belátható, hogy egy zárt módon minden csúcsának még indexek, és nyitott - pontosan két páratlan (ez a kezdet és a vég, az út). A tény az, hogy ha a csomópont nem a kezdet és vége, jött rá, mi kell majd belőle - így hány élek szerepelnek benne, mint sok belőle, de csak annyi bejövő és kimenő élek még . Ha a kezdeti csúcs egybeesik a végén, ez is egy index akár hány széleit úgy jött ki, és ugyanazt a számot beírni. És ha a kiindulási pont nem esik egybe a vég, a páratlan indexek: a kiindulási pontot kell egyszer kijutni, majd ha visszatér, majd hagyjuk újra, ha vissza -, hogy hagyja megint, stb.,. és a végén el kell jönnie, és ha ki belőle, majd kimegy, akkor meg kell, hogy menjen vissza, és így tovább. d.
Ahhoz, hogy a gróf unicursal, az szükséges, hogy minden csúcsának még indexek, illetve a csúcsok száma páratlan index megegyezik a kettő.
Most nézd meg megint a grafikont a probléma Königsberg híd.
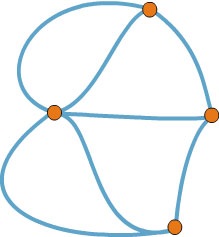
Ábra. 5. szám Königsberg híd
Számolja az indexek a csúcsok és győződjön meg róla, hogy nem lehet unicursal. Ezért nem kap, ha azt szeretné, hogy megkerülje az összes hidat.
Felmerül a kérdés: ha van egy gráf csúcsok páratlan index, vagy éppen két ilyen csúcs, vagy gróf feltétlenül unikursalen? Lehetőség van, hogy szigorúan bizonyítani, hogy igen! Így unicursality egyedileg kapcsolódó csúcsok száma páratlan index.
Feladat: Építsd a rendszer Königsberg híd másik híd - ahol csak akar -, hogy a kapott hidak révén kikerülhető lenne látogató minden pontosan egyszer; valóban végre ezen a módon.
Itt van néhány több grafikon - gróf magad vertex indexek, és ha lehetséges, próbálja meg elkerülni őket, „felemelése nélkül ceruzát a papírról.”
1 Modell grafikonok unicursality
Most egy másik érdekes tény: kiderült, semmilyen rendszer területekre, hidak kötik össze lehet kerülni, ha meg akarjuk látogatni minden híd pontosan kétszer! Próbálja bizonyítani magadnak.
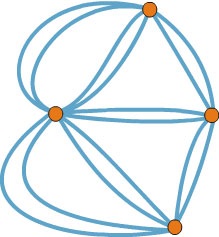
Ábra. 6. szám Königsberg híd dupla száma hidak unikursalen