közelítő számítások
A gyakorlatban, folyamatosan foglalkozunk közelítő értékek, egyenletek, képletek építeni parcellákon pontot, távolítsa el a gyökereit a számok, egyenletek megoldására, stb elmélete, a közelítő számítások, ami manapság gyorsan fejlődő, különösen fontos módszerek hasznos .. megoldására sokféle matematikai problémákat. Mi azt mondjuk, néhány ilyen módszereket.
Kerületi hossza számítás segítségével megduplázva képletek - specifikus példája az algoritmus megszerzésére közelítő értékeit a számot π. Ez a módszer érdekes történeti szempontból, hiszen talán az egyik legrégibb módszere a közelítő számítások. Formula megduplázása kötődik hosszúságú oldalakkal és egy N- a2n helyes és 2n-szögek írt kör (átmérője egyenlő 1):
és lehetővé teszi kezdve egy szabályos hatszög, amelynek oldalhossza egyenlő 1/2, kiszámításához a sorozat A12. A24. A48. ... amíg eljutunk egy értéket kerülete megfelel egy adott pontossággal. Lehetőség van annak bizonyítására, hogy
π - nan <6/n 2. n ≥ 3.
Ez az egyenlőtlenség lehetővé teszi, hogy ne csak megállapítani, hogy a folyamat konvergál (azaz π - .. Nan → 0, ha n → ∞), de kiszámítására és tervezés előre. Tehát, ha azt akarjuk, hogy biztosítsák a pontos számítás, egyenlő 10 -3. elegendő, hogy n, hogy a következő egyenlőtlenség 6 / n 2 <10 −3. т. е. n> √6000, vagy n ≥ 78> √6000.
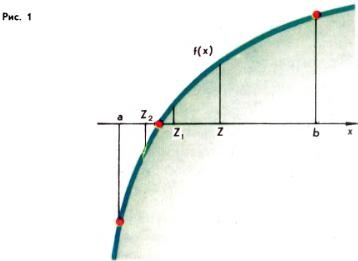
Fork módszerre megtalálni a gyökereit az f (x) = 0 a folyamatos f, meglehetősen általános. Legyen f meghatározását, valamint folyamatos a [a, b], hogy csak egy gyökér és f (a) <0, f(b)> 0. Tekintsük értéke az f (z), ahol z = (A + B) / 2 - középső szegmenst [a, b]. Ha f (z) = 0, akkor Z - kívánt gyökér. Ha f (z) ≠ 0, akkor a két szegmens [a, z] és [Z, b] egyikét választja ki, amelyek esetében a értéke az f függvény a végein különböző jeleket (az ábrán. Az 1. ábra egy szegmens [a, z] ), és jelöljük [a1. b1] így f (a1) <0 и f(b1 )> 0. Ha most egy pontot z1 = (A1 + b1) / 2, majd ismét, vagy F (Z1) = 0 vagy F (z1) ≠ 0. A második esetben a két szegmens [a1. z1] és [z1. b1] válassza ki az egy végein, amelyek az f függvény feltételezi értékei különböző jelek (ábra. 1, [A2. B2] = [a, z1]). Ha továbbra is ezt a folyamatot, ő vagy letörik egy bizonyos szakaszában, vagy azt, hogy egy szekvencia beágyazott időközönként [a, b], [a1. b1] [a2. b2], ..., amelyre egy ≤ an + 1
Ezen kívül van a egyenlőtlenségeket:
amely lehetővé teszi, hogy a menetrend kifizetések egy adott pontossággal.
Alkalmazása a származék a viselkedésének tanulmányozása funkció lehetővé teszi, így sok hasznos képletek a közelítő függvények értékeit. A származékos ügylet definíciójának, ebből az következik, hogy kis lépésekben Ax érv x0 az f függvény tudjuk írni a közelítő egyenlőség
Geometriailag ez azt jelenti, hogy közel az a pont x = x0 felrajzoljuk az y = f (x) grafikon helyére egy érintőleges a grafikon y = f (x) a ponton az abszcissza x = x0 (ábra. 2).
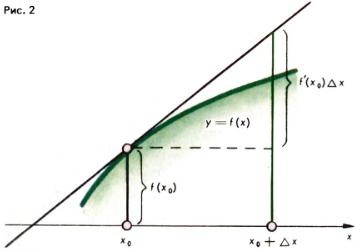
Például, a közelítő értékeket kapjuk (hatásos kis Ah):
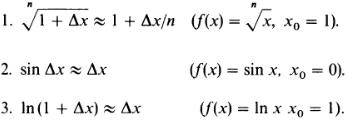
Módszer tangens Newton közelítő megoldások az egyenletek az f (x) = 0 a következő. Tegyük fel, hogy az f függvény egy egyetlen gyökere intervallumban c] a, b [és differenciálható minden pontban intervallumban] a, b [, és F „≠ 0 ebben az intervallumban. Vegyünk egy tetszőleges pont x0 ∈] a, b [, és írni az egyenlet az érintő a f grafikonja a ponton az abszcissza x = x0.
Grafikonok az f (x) és annak érintője közel állnak egymáshoz kis x - x0. és ezért természetes, hogy elvárják, hogy a metszéspont x1 grafikus érintője az X-tengely közelében kell elhelyezni, hogy a gyökér a C (ábra. 2). Van:
Folytatva ezt a folyamatot, kapunk egy szekvenciát (xn) pontok által meghatározott képlettel
Köztudott, hogy van még az egyenlőtlenség
ahol A> 0 - állandó, független n. Ez az egyenlőtlenség azt mutatja, hogy még egy kellően kis n kapott megfelelő pontossággal közelítés.
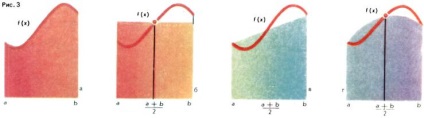
Hozzávetőleges számítás területek (integrálok) íves trapéz (3A.) Alapul egyszerű geometriai megfontolások. Ha az [a, b], a Ha helyett a funkció táblázatot a [a, b] nem a vonalszakasz, és a grafikon a parabola (ábra. 3 g) egy becsült S hogy egy görbe vonalú trapéz által határolt terület az ív a parabola, megkapjuk képletű Integrálszámítás lehetővé teszi, hogy pontosabban kiszámítani a területet a görbe vonalú trapéz.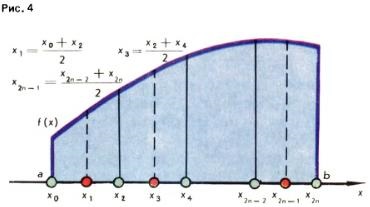
Ahhoz, hogy a lehető legkisebb hiba a közelítő számítások S, az intervallum-ból b osztani a pre 2n egyenlő részre. Ezután az ív generált y = f (x) van felosztva n alkatrészek (ábra. 4). Ha most minden egyes ilyen kis ívek a korábbi módszerek közelítést alkalmazzanak a terület S kapunk közelítő értékeit összegek területek n íves trapezoid; van:
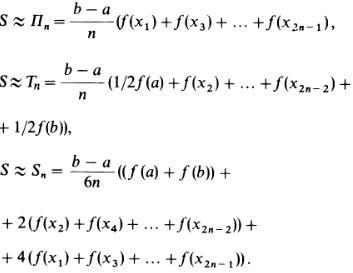
Az első két képlet alapján kapják nevüket téglalapok és a trapéz szabály, és az utolsó - a Simpson nevében a brit matematikus T. Simpson (1710-1761).
Hiba becslések ezekben közelítő képletek kiszámítása a gyakorlatban az alábbiak. Kiválasztott n szám, 4 többszöröse, és S képlet alapján Simpson (pontosabb a három) a pontok száma n és n / 2 (Sn és Sn / 2), és kb segítségével meghatároztuk a számítási hiba arányt