A Laval fúvóka vizsgálata
hozzon létre egy 3D fúvóka modellt
SW fúvóka szimuláció SW Flow szimulációval
elemezzék az eredményeket
A Laval fúvóka (vagy a konvergáló-bővítő fúvóka) egy középső csatorna, amely úgy néz ki, mint egy homokóra. Segítségével felgyorsítja az áthaladó gázáramot, hogy a sebesség gyorsabb legyen, mint a hangsebesség. Széles körben használják bizonyos típusú gőzturbinákon, és fontos része a modern rakétamotoroknak és a szuperszonikus sugárhajtású motoroknak.
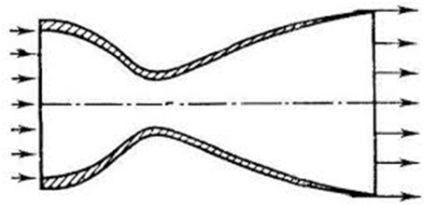
A fúvókát 1890-ben a svéd feltaláló Gustave de Laval fejlesztette ki.
A fúvóka működtetése a gázáram különböző tulajdonságaira épül, szubszonikus és szuperszonikus sebességnél. A szubszonikus áramlás sebessége növekszik, ahogy a csatorna szűkül, mivel a tömegáram állandó. A gázáram egy de Laval-fúvókát izentropikus (gáz entrópia közelítőleg állandó). Subsonikus sebességnél a gázáram összenyomható; a hang (alacsony nyomású hullám) egy ilyen áramláson át terjed. Közel a „nyak” a fúvóka, ahol a keresztmetszeti területe a legkisebb, a helyi gázsebesség válik hang (Mach-szám M = 1) Miután a fúvóka keresztmetszeti területe növekedni kezd, a gáz továbbra is bővíteni, és a gázáram gyorsult szuperszonikus sebességgel, ahol a hanghullám halad az ellenkező irányba a gázon keresztül (M> 1).
Laval fúvóka jár csak abban az esetben, hogy a tömegáram a fúvókán keresztül elegendő, különben szuperszonikus sebesség nem érhető el. Ezenkívül a fúvóka táguló részének kimeneti nyílásánál a gáznyomás nem lehet túl kicsi. Mivel a nyomás nem adható át ellen szuperszonikus áramlás, a kimeneti nyomás lehet lényegében környezeti nyomás alatti közeg, amelyben lejár gáz, de ha ez túl kicsi, akkor az áramlás megszűnik, hogy egy szuperszonikus vagy patak elválasztják a divergens része a fúvóka, alkotó instabil áramlás, amely "tapsolhat" a fúvókában, és megsérülhet. A gyakorlatban, a környezeti nyomás nem lehet több, mint 2,7-szer nagyobb, mint a nyomás egy szuperszonikus gáz, ezen feltételek mellett, a szuperszonikus áramlás a fúvóka távozhat.
A gázmozgás matematikai leírásához az ideális gázállapot egyenletét és az Euler-egyenletet alkalmazzuk. Számukra egy ilyen kulcsegyenletet vonhatunk le:
ahol a mennyiségek a gáz sűrűségének és sebességének koordinátáinak relatív mértékét jellemzik. Ezenkívül az (1) egyenlet azt mutatja, hogy ezeknek a mennyiségeknek az aránya megegyezik a Mach számának négyzetével (a mínusz jel a változások ellentétes irányát jelzi: a sebesség növekedésével csökken a sűrűség). Így a szubszonikus sebességnél (M <1) плотность меняется в меньшей степени, чем скорость, а на сверхзвуковых (M> 1) - éppen ellenkezőleg. Amint később látható, ez határozza meg a fúvóka szűkítő-bővítő alakját.
Mivel a gáz tömegáramlása állandó:
,
ahol A a fúvóka helyi szakaszának területe
.
az egyenlet mindkét oldalát differenciálva x-vel. kapunk:
Az (1) -ból (2) való helyettesítés után végül:
A (3) bekezdésből látható, hogy amikor a gázsebesség a fúvókában nő, akkor a kifejezés jele pozitív, következésképpen a származék jele a kifejezés jele.
Amiből az alábbi következtetéseket vonhatjuk le:
A szubszonikus gázsebességnél (M <1), производная – сопло сужается
A szuperszonikus gázsebességnél (M> 1) a származék - a fúvóka kibővül.
Amikor a gáz a hang sebességével mozog (M = 1), a származék - a keresztmetszeti terület - eléri a szélsőséget. azaz a fúvóka legszűkebb része, a kritikusnak nevezik.
Tehát a fúvóka kúpos, szubkritikus részében a gáz szubszonikus sebességgel mozog. A fúvóka legkeskenyebb, kritikus szakaszán a gáz helyi sebessége eléri a hangsebességet. A bővülő, túl kritikus szakaszon a gázáram a szuperszonikus sebességgel mozog.
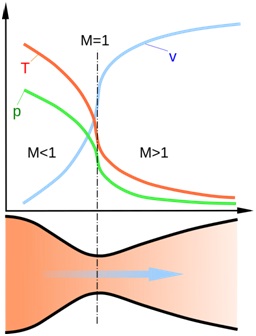
A fúvóka mentén mozog, a gáz kitágul, hőmérséklete és nyomása csökken, és a sebesség növeked. A gáz belső energiája átalakul az irányított mozgás kinetikus energiájává. A hatékonyságát ez az átalakulás, bizonyos esetekben (például, a fúvókák a rakéta motorok ma) haladja meg a 70%, ami messze meghaladja a tényleges hatékonyságát termikus motorok más típusú. Ez annak a ténynek köszönhető, hogy a munkaközeg nem továbbítja a mechanikai energiát közvetítő (a lapátok a turbina vagy dugattyús). Az átadás más termikus motorjaiban jelentős veszteségek vannak. Továbbá a gáz áthalad a fúvókán nagy sebességgel, nem sikerül átadni falait jelentős mennyiségű hőt, ami adiabatikus folyamat. Más típusú, tényleges hőgépekben a szerkezet fűtése a veszteségek lényeges részét képezi. Például egy autómotor jobban működik a hűtőberendezésen, mint a kimeneti tengelyen.
A Laval fúvóka munkájának bemutatása. Amint a gáz a fúvókán át mozog, abszolút T hőmérséklete és a nyomás p csökken, és a V sebesség növekszik
A munka teljesítményének sorrendje
Szilárd fúvóka-modell készítése SW-ben:
Fúvóka-modell létrehozása:
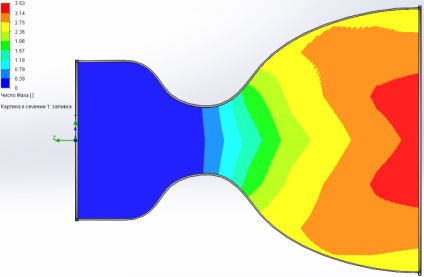
Nyomásmintázat a fúvóka felületén:
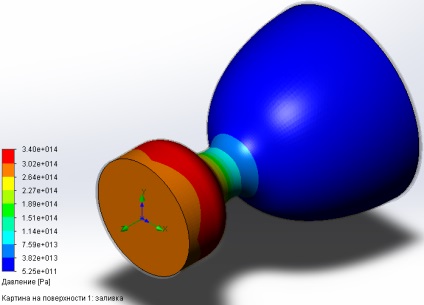
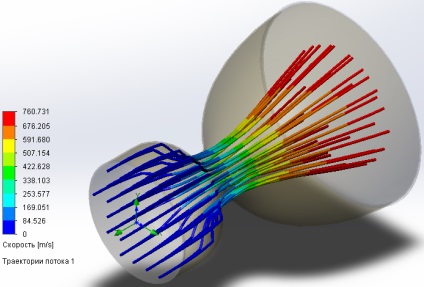
A Flow szimuláció használatával grafikonokat is létrehozhat, amelyek egy paraméter eloszlását mutatják a tengely mentén, majd exportálják ezeket a gráfokat MS Excel-be.
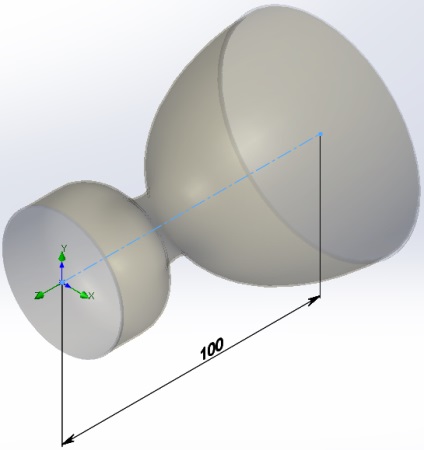
A fúvóka középvonalát háromdimenziós vázlatként állítjuk elő. A középvonal hossza megegyezik a fúvóka hosszával; 100 mm.
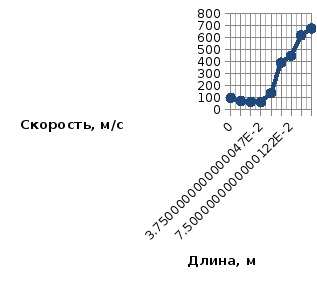
A sebességváltozás diagramja a fúvóka hosszán A nyomásváltozás diagramja a fúvókahossz mentén

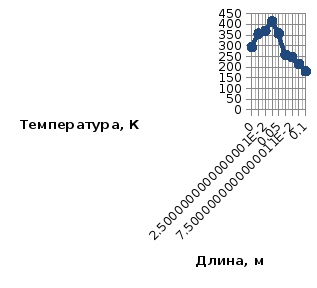
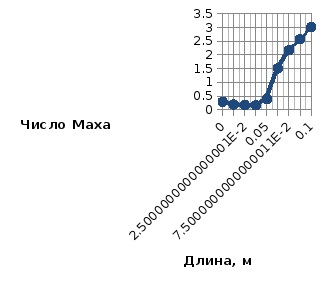
A hőmérsékletváltozás grafikonja a fúvóka hosszán A Mach számváltozás diagramja a fúvókahossz mentén
Mi az a Laval fúvóka?
Milyen eszközöket használtak a Laval fúvókák?
Mi a fúvóka alapelve?
A fúvóka működésének feltételei?
Mi az alapja a fúvókában előforduló folyamatok matematikai leírásának?
Mi az egyenletek (1) és (3) fizikai jelentése?
Mi a szubkritikus, kritikus és szuperkritikus terület?
Mi a Laval fúvóka hatékonysága?
A megoldás eredménye összhangban van az elméleti adatokkal? Mutassa be a konkrét példákat.
Független munkaszám 3