A hibák összegzése 1

A hibák összegzésénél a következőket kell vezérelni:

1. Rendszeres hibák -

, Ha ismertek és kellőképpen jól definiáltak, azokat algebraikusan összegzik, azaz. figyelembe véve a megjelöléseket

2. Véletlenszerű hibák, az átlagos négyzet becsléseik összegzése a kölcsönös korrelációs kapcsolatok figyelembevételével történik, a valószínűségi elméletből ismert függőség alapján

(1.44) ahol

- két véletlen változó összegének varianciája; és - Véletlen változók diszperziója; r a korrelációs együttható, amelynek lehetséges értékei -I-től + 1-ig terjedő intervallumban vannak.

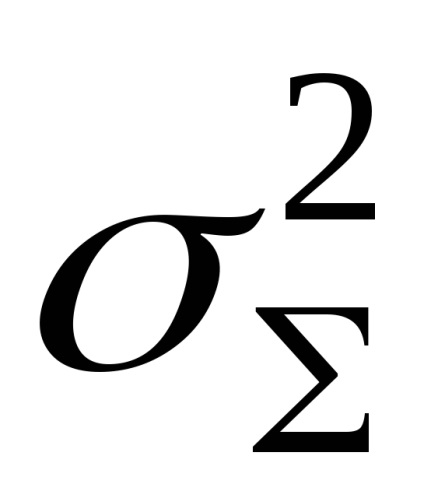
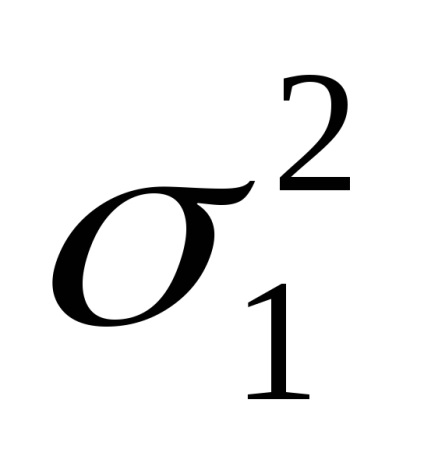
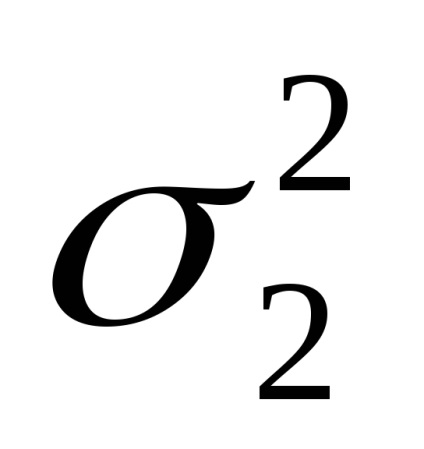
Összes gyökér közép négyzetes hiba

Általában nincs információ a korrelációs intézkedésről, így a gyakorlatban két szélsőséges esetet kell figyelembe venni: r = 0, r = ± 1. Ha r = 0, akkor a véletlenszerű hibák statisztikailag függetlenek (nem korrelált), és a hibákat geometriailag összefoglaljuk:

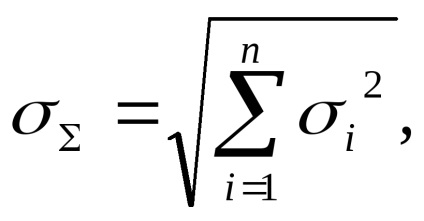
ahol

- a forrás által okozott hiba root-mean-square error.

Ha a véletlen hibák erősen korreláltak (r = ± 1), akkor a mérési eredmények között funkcionális kapcsolat van. Ebben az esetben, ha r = + 1,

vagy kivonjuk, ha r = -1

A szisztematikus hiba összegzése véletlenszerű hibával történik, figyelembe véve a korrelációs kapcsolatokat ugyanazon elv szerint, mint a véletlenszerű hibák összegzése.

I.I3. A közvetett mérések hibái

Közvetett méréseknél a keresett fizikai mennyiség értékét a mért mennyiséghez tartozó egyéb mennyiségek összehangolt mérésével állapítják meg egy ismert funkcionális függőséggel. Ezeket a mennyiségeket mérhető érveknek nevezik. Az érvek értékeit leggyakrabban a közvetlen mérések eredményeként találják meg, de néha közös, kumulatív vagy közvetett mérések eredményeként. Ezért a probléma merül fel: meghatározni egy függvény hibáját az adott hibákhoz az argumentumokban.

A Q mért értéke a dependencia által mért értékekkel függ össze

Vannak olyan esetek, amikor a Q és a Qi implicit kapcsolat van.

A funkcionális függőségnek köszönhetően a közvetett méréseket a mért mennyiség és az érvek közötti lineáris összefüggéssel különböztetik meg

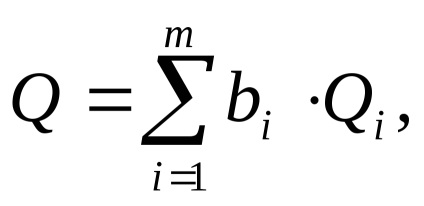
nemlineáris függőséggel

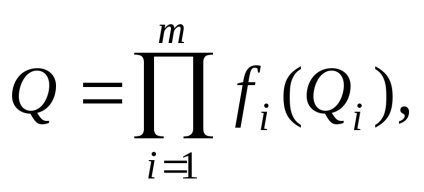
vegyes típusú függőséggel

Becsüljük az eredményt

és a közvetett mérés pontatlanságai D, az eredmények becslése és pontatlanságaAz érvek közvetlen mérései.

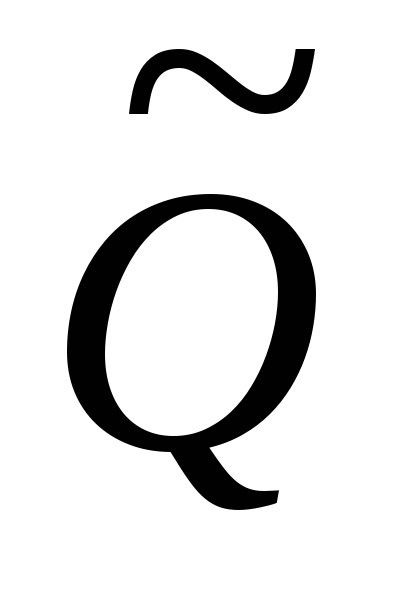
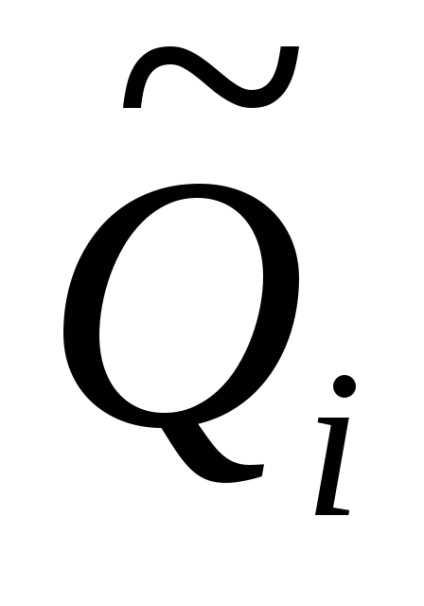
Legyen minden Qi érvet egy becsléssel

és pontatlanság, amely az i-edik argumentum teljes hibájának megvalósítását jelenti. A közvetett mérés egyenletébe helyezzük az értéket és bontsa Taylor-sorozatba. Elmulasztva a feltételeket magasabb fokkal, mint az első

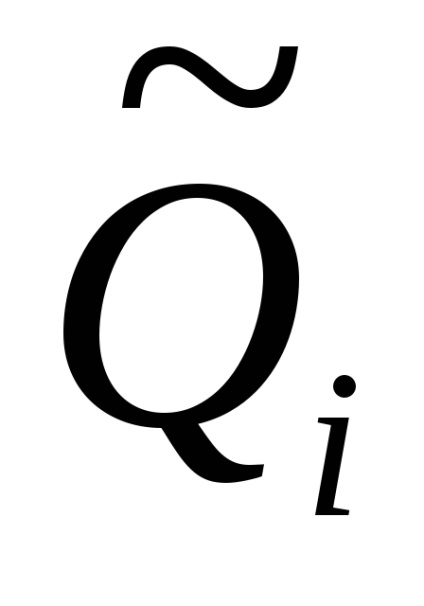
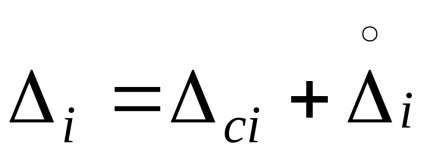
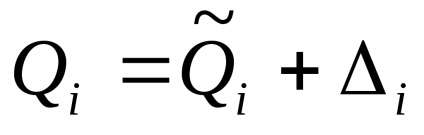
Az (1,49) -tól az eredmény becslését kapjuk

és a közvetett mérés hibái

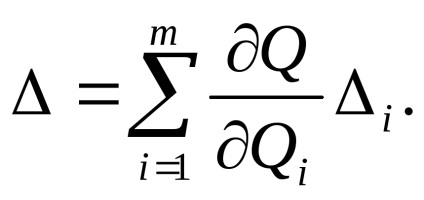
Az ilyen vizsgálat elfogadhatóságát ellenőrizni kell. származékok

az úgynevezett befolyási együtthatók, és a kifejezések- részleges hibák.

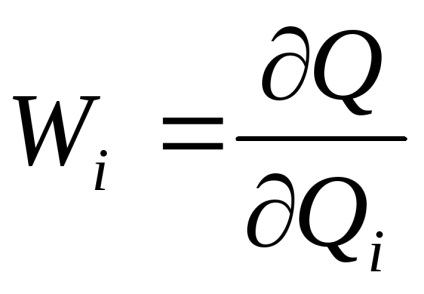
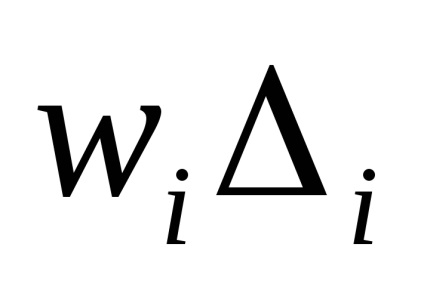
Véletlenszerű hibák mérlegelése. Ráadásul az összes Qi becslésében lévő hibák szisztematikus összetevőit feltételezik, hogy állandóak. Jelezzük a közvetett szándék véletlenszerű hibájának átlagos négyzetes értékének becslését

ahol

- egy közvetlen mérési argumentum eredményének varianciájára vonatkozó becslés,

- a k és l érvek mérése során a véletlen hibák közötti korrelációs koefficiens becsléseaz intervallumban van.

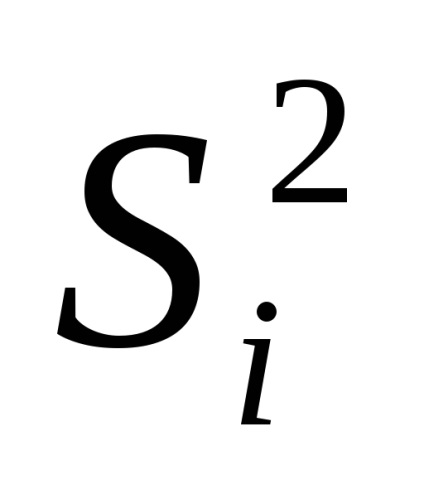
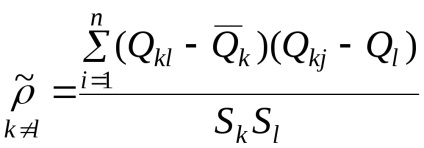
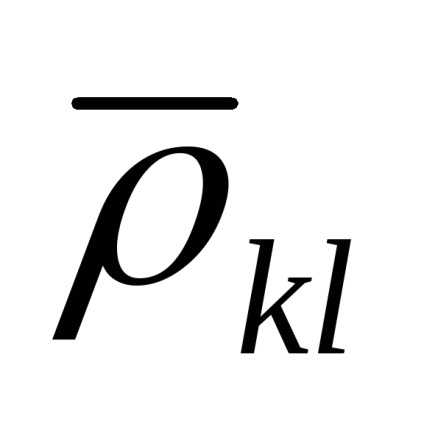
Ha az érvek dimenzióit nem egyidejűleg teszik különféle mérési módszerekkel, akkor a korrelációs együttható nullához közelít, és

Az átlagos négyzetbecslés bevezetett új jelölése hangsúlyozza, hogy a megfigyelések eredményeinek eltéréseit használjuk az érvek közvetlen mérésére szolgáló egyenletekben.

Állandó szisztematikus hiba Δc az indirekt mérés eredményéből

Ha ismeretlen rendszeres hibák jelei ismeretlenek, akkor az indirekt mérések eredményének szisztematikus hibája a következőképpen alakul:

amelyet határnak neveznek.

A relatív hibák kiszámításánál  a c és

hivatkozzon az indirekt mérések eredményére.

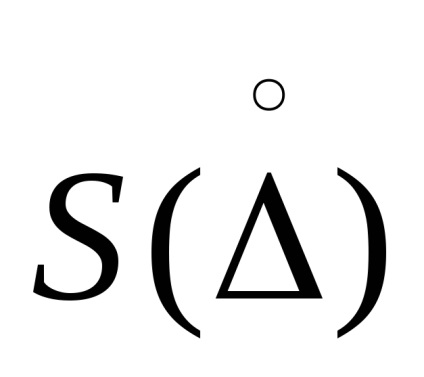
Meg kell jegyezni, hogy a relatív hiba közvetett mérések egyes esetekben kerülhet nagyon nagy érték-CIÓ, például az alábbi függvénnyel Q = Q1 -Q2 a kis értékei a különbség

.

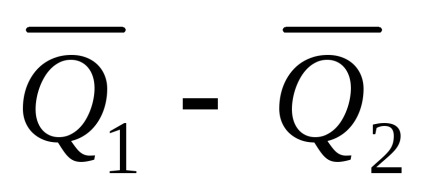
Közvetett mérésekkel olyan módszerek kifejlesztése szükséges, amelyek biztosítják a közvetett mérés hibájának megőrzését a megengedett határértékeken belül. Ez a Ql és Qk értékek kiválasztásával érhető el. amelynél a relatív hiba nem haladja meg a megengedett határértékeket; olyan mérési módszerek alkalmazása, amelyekben a közvetett mérés egyenlete nem tartalmaz kis különbségeket; a módszerek és a mérési eszközök kifejlesztése, közvetlen közvetett mérést biztosítva a közvetett helyett.

Vizsgáljuk meg, hogy a véletlenszerű hiba konfidencia intervallumát, valamint a közvetett mérések eredményének nem kizárt szisztematikus hibáira vonatkozó határértéket vagy konfidenciaintervallumot becsüljük.

A véletlen hiba eredménye közvetett mérés, de nem tudjuk vállalni normális eloszlású valószínűségi változó, akkor is, ha a kifejezések eloszlása ​​eltér a nor-mal, de a kifejezések száma nem kevesebb, mint 4 és nem Domini -5-al hiba.

A véletlen hiba bizalmi értékeit p a képlet határozza meg

tényező

, ahol a Laplace függvényből származik (a függelék 2. táblázata).

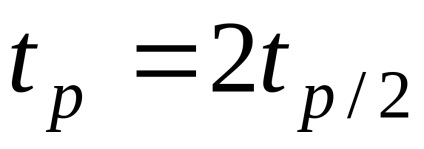
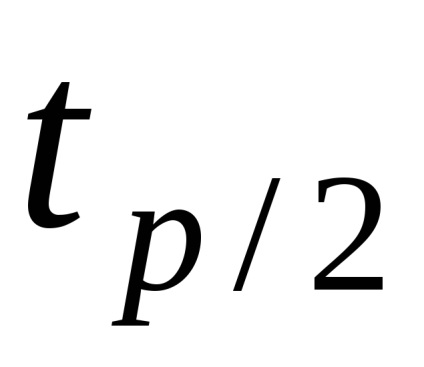
Mint fentebb említettük, a nem kizárt módszeres hibák véletlenszerű változóknak tekinthetők. Az egyes komponensek esetében megtalálhatók a i határai, és ha lehetséges az eloszlás és becslés felbontásának igazolása

, definiálják őket

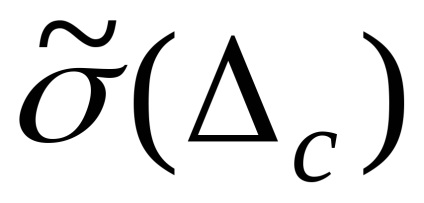
ahol k a feltételezett bizalmi valószínűség által meghatározott együttható, amely a bizalmi valószínűségek esetén 0,9; 0,95; 0,99 0,95; 1,1; 1.4.

A teljes mérési hiba határait a GOST 8.207-76 [7] szerint becsüljük meg.

Kapcsolódó cikkek

• A hibák összegzése