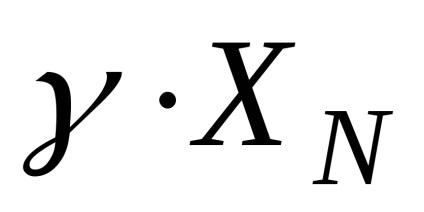Pontossága közvetlen mérés egyetlen
3.5.1. Egységes mérés pontos becslési hiba
A legtöbb mérés - egyszeri. A mérési eredmények közé instrumentális, módszeres és személyes komponensek, amelyek mindegyike lehet szisztematikus és véletlenszerű.
Szisztematikus hibák egyik vagy másik úton próbálják kizárni marad IPV és véletlenszerű hibák.
Határok NSP számítjuk ki a korábban megadott képlet (3-8).
Ha az ismételt mérések a korábbi ismert konfidenciahatárait véletlen hiba e, akkor hozzáadjuk a NRS az NRS minősül véletlen hiba. Összesen korlátozó véletlen hiba Δ formula határozza meg:
Ha az e értéke ismeretlen, úgy tartják, hogy ε = 0.
Az eredmény, hogy egyetlen mérés R, amikor a mért érték x jelentette formájában:
3.5.2. Egy mérés egy hozzávetőleges becslési hiba
Körülbelül mérési hiba becslése „top”, tudván, a legnagyobb megengedett hiba mérésére Δpr útlevelek. Gyakran előfordul, hogy ennek eredményeként a mérési hiba határérték figyelembe Δpr = ± (fél áron az egység osztás), és néha Δpr = ± (osztódó egységár).
Pontosság közvetett mérések
Meghatározása indirekt mérési pontban megadott 2.1. Számítások közvetett mérési hibák lehet csökkenteni, hogy egyszerű szabályok [4], jelezve: R-eredmény közvetett mérések; A, B, C-eredményeként direkt mérésekkel a a paramétereket, melyek alapján kerül kiszámításra R; Δ - abszolút mérési pontosság bármilyen mennyiségben, például ΔR, AA, stb.;. δ - relatív hiba értékeket, mint például: δR = ΔR / R; AA = Aa / A és t. d.
Ha R = A + B vagy R = A - B, majd
t. e. az abszolút hibája az indirekt mérés összege az abszolút hibát a közvetlen mérés.
Ha R = A · B vagy R = A / B, akkor a hiba a relatív -ról:
Ha R = kA. ahol k - faktor,
ahol | k | - az abszolút értéke az együttható.
Példa. A disszipált teljesítmény az egész R ellenálláson egy R ellenállás egy aktuális egyenlő a I. I2 · R. Ezután a relatív hiba AP = 2 · Aj + δR. Az abszolút hibája az eredmény AP = AP / P. Az eredmény kerül bemutatásra a következő formában: P? P ±.
Hiba oszlopdiagram eszközök
Ha a méréseket széles körben használják oszlopdiagram (analóg) eszközök [9]. Részletek skálán az egyik eszköz ábrán látható. 3.4. Az alsó rész a 2. ábra a skála az eszköz osztály, itt vannak elhelyezve, és egyéb speciális karaktereket.
P
Az abszolút hiba Δ mérő eszközzel határozzuk meg a különbséget leolvasott mérési X és a referencia leolvasott Hat:
Ábra. 3.4. A készülék típusától skála
Az abszolút hiba a háromdimenziós mennyiséget. A módosítás azt az abszolút hiba ellentétes előjelű.
Relatív hiba által meghatározott egyenletek:
Relatív hiba dimenziómentes és ki lehet fejezni tizedes tört vagy százalékos.
Relatív hiba arányaként definiáljuk a redukált abszolút hiba a műszer egy normalizált skála érték (a felső határ a mérési) XN:
Mivel a relatív hiba százalékosan határozza meg a pontossági osztály az eszköz.
Példa. Mert látható. 3.4 A készülék 2. osztály pontossági hiba csökkent γ = 2% (0,02). Ezután az abszolút hiba jelzések Δ =