Bombázó merülés a cél szögben 60 fok, hogy a horizont

Állapota a problémát:

Bombázó merülés a cél szögben 60 ° a horizonthoz sebességgel 540 km / h, és esik egy bomba magasságban 600 m. Egy bizonyos távolságra a cél a vízszintes irányban van szükség, hogy kiadja a bomba úgy, hogy elérje a célt?

№1.6.13 feladata a „Collection feladatok előkészítése a felvételi vizsgák a fizika UGNTU”

\ (\ Alpha = 60 ^ \ circ \), \ (v_0 = 540 \) km / h, \ (h = 600 \) m, \ (L -? \)

Megoldás:

Meg kell érteni, hogy a bomba eltér a rakéták, hogy az nem a motor, így a bomba sújtotta a hely teljesen tulajdonságai határozzák meg a mozgás bombázó. Abban az időpontban. amikor a bombázó ledobta a bombát, akkor ugyanaz lesz a sebességvektor a gépre. Ennek megfelelően, a jelen mintát ezt a problémát.

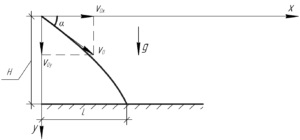
Írunk az egyenleteket a mozgás bomba előrejelzéseket az \ tengely (x \) és \ (y \).

Közlemény a második egyenletben a „plusz” jel, azért van, mert a \ (v_x \) és \ (g \) azonos irányba.

Engedje meg, hogy mennyi idő fog csepp a bomba, ezt használjuk a (2) egyenlet és megoldani egy másodfokú egyenlet:

\ [G + 2 \ sin \ alpha \ cdot t - 2h = 0 \]

\ [D = 4v_0 ^ 2 \ alpha + 8gh \]

Természetesen nyilvánvaló, hogy egyik gyökerét negatív, a gyökere a következő:

Számításaink időt azáltal, hogy az összes ismert értékek az SI-rendszerben. Megmutatjuk, hogyan lehet lefordítani egy 540 km / h m / s.

Behelyettesítve ezúttal egyenlet (1), és megtalálni a választ:

\ [L = \ cos \ alpha \ cdot t \]

\ [L = 150 \ cdot \ cos 60 ^ \ CIRC \ cdot 4 = 300 \; m. \]

Válasz: 300 m.

Ha tetszik a probléma és annak megoldása, akkor ossza meg ismerőseivel Ezekkel a gombokkal.

Kapcsolódó cikkek

• Zuhanóbombázó akik nem merültem - Honvédségi Szemle