Az inverz probléma az elmélet hibák
A gyakorlatban gyakran van szükség ahhoz, hogy megoldja a problémát inverz: mi legyen a abszolút hiba a függvény érveit, hogy az abszolút hiba függvény nem haladja meg egy előre meghatározott értéket.
Hagyja, hogy a maximális értékét abszolút hiba van megadva.
Feltételezve, hogy az összes feltételt egyenlő, van:
Abban az esetben, ha a korlátozó abszolút hiba az érvelés ugyanaz, akkor:
7.1. A sugár a henger alap; a magassága a hengerben. Mi szükséges, hogy meghatározzuk az abszolút hiba R és N, hogy a henger térfogata V lehet kiszámítani pontossággal 0,1 m?
A térfogatot képlettel számítottuk ki. Behelyettesítve a nyers adatokat, megkapjuk kb:
Ennélfogva, a T f = 3, akkor a következő képlet segítségével kiszámítására a bűnös-ness függő funkció három változó ..:
Táblázat hibák értékei elemi függvények.


8. Feladatok laboratóriumi munka 1-es szám:
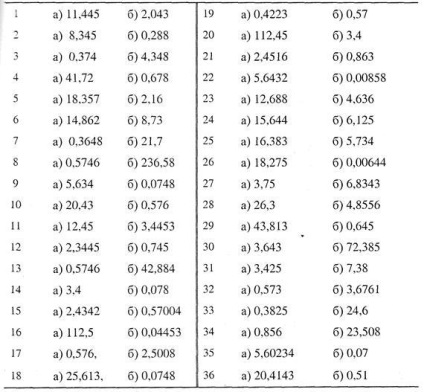
8.1. Feladatok (saját) .Nayti korlátozzák az abszolút és relatív hiba számok, ha azok csak a valós számadatok (asztal beállítási lehetőségek).
a) a szűkebb értelemben vett; b) a tág értelemben vett.
Tablitsa.Varianty feladatok elvégzésére önálló munka
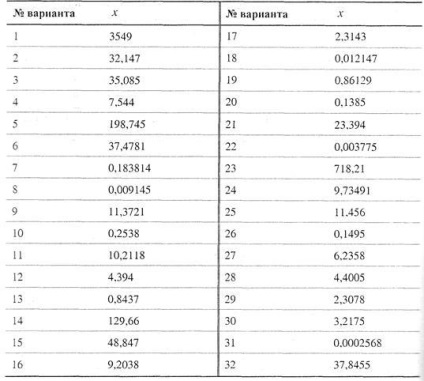
8.2. Feladatok az önálló munkavégzésre. A szám x (lásd táblázat.), Az összes számjegy helyes a szó legszorosabb értelmében, kerekítve három szignifikáns adatot. Az eredmény kiszámításához a határokat az abszolút és relatív hiba. A rekordszámú. adja meg a szám helyes számjegyet abszolút és relatív hiba.
Tablitsa.Varianty feladatok elvégzésére önálló munka
8.3. Számítsuk ki a z értéke (táblázat) adott értékeknél a számok a. b és c segítségével szisztematikus vizsgálatát abszolút hibát minden egyes használat után, valamint a határokat módszer. Keresse abszolút és relatív hibája z és meghatározza azokat a szám helyes számjegy z, és ha a számok. b és c igazak szigorú értelemben.
Táblázat. Változatok a feladatok elvégzésére önálló munka




8.4. A következő feladatokat módszerével határok.
8.4.1. A hossza a légi útvonal két pont között egyenlő S km. Plane megoldja ezt az időbeli távolság t h Határozza meg határait az átlagsebesség a repülőgép, ha:.; .
8.4.2. Tűzhely tervezett feszültség V. Keresse spirál elektromos ellenállás, azt tudjuk, hogy át kell haladnia a jelenlegi 5 ± 0,1 A.
8.4.3. A réz bár egy térfogata V m (). Megtalálja a tömege, ha a réz sűrűsége kg / m teszi.
8.5. Az alábbi feladatok elvégzéséhez használja az általános képlet hibát.
8.5.1. Fajlagos elektromos ellenállása a fém kerek vezeték hossza L m d mm keresztmetszetű és az Ohm R ellenállás adja :. Find. ha: L = 12,50 ± 0,01 m, d = 2,00 ± 0,01 mm, R = 0,068 ± 0,0005 ohm, = 3141 ± 0,001. Határozzuk meg a relatív hiba.
8.5.2. Egy függőleges, hengeres tartály folyadékkal töltött. Ahhoz, hogy mennyi idő szükséges, hogy üres a tartály egy kör alakú lyukat az alján. Tartály átmérője D = 1 ± 0,01 m, a folyadék szintje magassága H = 2 ± 0,02 M, alsó furat átmérője d = 0,03 ± 0,001 m, az áramlási sebesség = 0,6 ± 0,02. Számítás (másodpercben) végezzük az alábbi képlet szerint:
8.6. Oldjuk meg a következő problémák az inverz probléma az elmélet hibák:
8.6.1. Abból, amit pontossággal kell mérni a kör sugara R = 30,5 cm, és hány számjeggyel számát korlátozni kell. hogy a terület egy kör volt ismert pontossággal 0,1%?
8.6.2. A hossza a derékszögű négyszög oldalával egyenlő. . Mi elismeri Timaya korlátozó abszolút mérési hiba ezen értékek ugyanaz mindkét fél számára, úgy, hogy az S felület a téglalap lehet meghatározni a limitáló abszolút hiba?
1. Mi az abszolút és relatív hiba?
2. Milyen hibák vannak besorolva?
3. Mit jelent az a szám, hű Egy egyszerű tág értelemben?
4. Milyen az kerekítési hiba számát?
5. Hogyan kell meghatározni a szám helyes számjegyek a relatív hiba hozzávetőleges számát?
6. Hogyan kell alkalmazni az abszolút és relatív hiba számtani műveleteket?
7. Hogyan értékeli az értékek elemi hibákat?
8. Hogyan megfogalmazni inverz probléma az elmélet hibák?
9. Milyen legyen az abszolút hiba a függvény érveit, hogy az abszolút hiba függvény nem haladja meg az előírt értéknek?
Bizonyos esetekben, a módszer a határok?