Formula gyökerei másodfokú egyenlet, a legnagyobb portál a tanulási
Formula gyökerei másodfokú egyenlet
Tegyük fel, hogy adott egy másodfokú egyenlet ax 2 + bx + c = 0.
Alkalmazható a három távú kvadratikus ax 2 + bx + c jelentése azonos átalakulások végzünk a 13. §, hogy bizonyította a tétel, hogy a függvény grafikonját y = ax 2 + bx + c egy parabola.
van
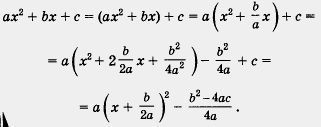
Tipikusan az expressziós b 2 - 4ac és betűvel jelöljük D nevezzük diszkriminánsa másodfokú egyenlet ax 2 + bx + c = 0 (vagy diszkriminánsa másodfokú polinom ax + bx + c).
Ennélfogva, a másodfokú egyenlet ax 2 + dx + c = G lehet átírni
Bármilyen másodfokú egyenlet lehet átalakítani, hogy a forma (1), kényelmes, mint látni fogjuk, annak érdekében, hogy meghatározzák a száma gyökerei a másodfokú egyenlet és megtalálni azokat gyökereit.
Bizonyítás. Ha D <0, то правая часть уравнения (1) — отрицательное число; в то же время левая часть уравнения (1) при любых значениях х принимает неотрицательные значения. Значит, нет ни одного значения х, которое удовлетворяло бы уравнению (1), а потому уравнение (1) не имеет корней.
Példa 1. egyenlet megoldását 2x 2 + 4 + 7 = 0.
Határozat. Itt, a = 2, b = 4, c = 7,
D = b 2 -4ac = február 4. 4. 2. 7 = 16-56 = -40.
Mivel D <0, то по теореме 1 данное квадратное уравнение не имеет корней.
Bizonyítás. Ha D = 0, az (1) egyenlet válik
- az egyetlen gyökere az egyenlet.
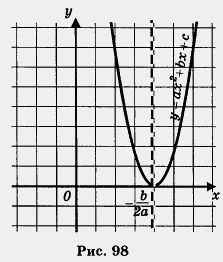
1. megjegyzés Emlékszel, hogy x = - - abszcissza a csúcsa a parabola, amely a függvény grafikonját az y = ax 2 + + velük? Miért
érték volt az egyetlen gyökere a másodfokú egyenlet ax 2 + dx + c - 0? „Koporsó” egyszerűen nyit: ha D - 0, ahogy korábban létrehozott
A grafikon a függvény egy parabola csúcsú pontban (lásd. Pl, Fig. 98). Ennélfogva, az abszcisszán a parabola csúcsa, és csak gyökér a másodfokú egyenlet D = 0 - ugyanazt a számot.
2. példa: megoldani az egyenletet 4x 2 - 20x + 25 = 0.
Határozat. Itt, a = 4, b = -20, c = 25, D = b 2 - 4ac = (-20) 2 - 4 • 4 • 25 = 400-400 = 0.
Mivel a D = 0, a 2. tétel, ez a másodfokú egyenlet van egy gyökér. Ez a gyökér által adott
2. megjegyzés megjegyzés, hogy a 4: 2 - 20x + 25 - egy tökéletes négyzet: 4x 2 - 20x + 25 = (25) 2.
Ha észrevettük meg azonnal, úgy döntöttünk, hogy az egyenlet a következőképpen: (2 - 5) 2 = 0, akkor 2 - 5 = 0, ami azt jelenti, x = 2,5. Általában, ha a D = 0, akkor
ax 2 + bx + c = - korábban jeleztük a Megjegyzés 1.
Ha D> 0, akkor a másodfokú egyenlet ax 2 + bx + c = 0 két gyökerei, amelyek a képletek
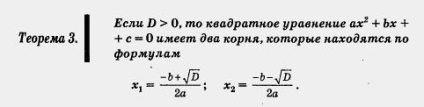
Bizonyítás. Átírása másodfokú egyenlet ax 2 + b x + c = 0 a (1)
tesz
A feltételezés, D> 0, akkor a jobb oldalon egy pozitív szám. Ezután, a (2) egyenletnek, hogy

Tehát, mivel a másodfokú egyenlet két gyöke:
3. megjegyzés: A matematikában ritkán fordul elő, hogy bevezette a kifejezés nem volt, képletesen szólva, világi indítéka. Vegye ki az új
fogalma - diszkrimináló. Emlékezz a „diszkrimináció”. Mit jelent ez? Ez azt jelenti, megalázás és magasztalás egy másik, azaz a különböző arányban
Különböző pyudyam. Mindkét szó (és diszkrimináló, és diszkrimináció) származik a latin discriminans - «diszkriminatív.” Diszkriminancia megkülönböztetést másodfokú egyenlet számának gyökereit.
3. példa: oldja egyenletet Sx 2 + 8x - 11 = 0.
Határozat. Itt, a = 3, b = 8, c = - 11,
D = b 2 - 4ac = 8: 2 - 4 • 3 • (-11) = 64 + 132 = 196.
Mivel a D> 0, a 3. tétel, ez a másodfokú egyenlet két gyökerei. Ezek a gyökerek által adott (3)
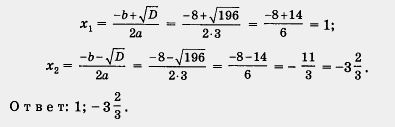
Sőt, te és én kidolgozott, a következő szabály:
Jellemzően az oldat egyenlet
ax 2 + bx + c = 0

Ez a szabály általános, hogy alkalmazható a komplett és inkomplett a másodfokú egyenletek. Azonban hiányos másodfokú egyenlet általában nem oldja meg ezt a szabályt, sokkal kényelmesebb dönteni, mint mi az előző részben.
4. példa megoldásához egyenletet:
a) 2 x + Sx - 5 = 0; b) - 9x 2 + 6x - 1 = 0; c) 2-X 2 + 3,5 = 0.
R e w n e) amennyiben egy = 1, b = 3, c = -. 5,
D = b 2 - 4ac = W 2 - 1 • 4 • (- 5) = 9 + 20 = 29.
Mivel a D> 0, akkor ez a másodfokú egyenlet két gyökerei. Ezek a gyökerek a következő képlettel (3)
b) A tapasztalatok azt mutatják, hogy sokkal kényelmesebb kezelni másodfokú egyenletek, melynek vezető együttható pozitív. Ezért az első szorozza mindkét oldalát -1 kapjunk
9x 2 - 6x + 1 = 0.
Ahol a = 9, b = -6, c = 1, D = b 2 - 4ac = 36 - 36 = 0.
Mivel a D = 0, akkor ez a másodfokú egyenlet van egy gyökér. Ez a gyökér által adott X = -. ennélfogva
Ez az egyenlet megoldható más módon: a
9x 2 - 6x + 1 = (Sx - IJ, kapjuk egyenletet (Sx - I) 2 = 0, azt találjuk, Sx - 1 = 0, azaz X = ...
c) ha a = 2, b = - 1, s = 3,5, D = b 2 - 4ac = 1 - 4 • 2 • 1 3,5 = - 28 = - 27. Mivel D <0, то данное квадратное уравнение не имеет корней.
Matematika - emberek praktikus, gazdaságos. Miért, azt mondják, hogy az ilyen hosszú uralma másodfokú egyenlet megoldása, akkor jobb, hogy írjon az általános képlet:
Ha kiderül, hogy a diszkrimináns D = b 2 - 4ac - negatív szám, akkor írj a képlet nincs értelme (jel alatt a négyzetgyök negatív szám), akkor nincsenek gyökerei. Ha kiderül, hogy a diszkrimináns nulla, megkapjuk
.. azaz egy gyökér (is mondják, hogy egy másodfokú egyenlet ebben az esetben két azonos gyökér:
Végül, ha kiderül, hogy b 2 - 4ac> 0, akkor megkapjuk a két gyökér x1 és x2. amelyek kiszámítjuk a ugyanazokat a képleteket (3), a fentiekben meghatározott.
A puszta száma ebben az esetben pozitív (mint bármely négyzetgyöke pozitív szám), és egy dupla jel előtt azt jelenti, hogy az egyik esetben (megtalálásában x1) egy pozitív szám hozzáadódik a számát - b és a másik esetben (megtalálása x2) Ön egy pozitív szám
olvasni a számot - b.
Van a választás szabadságát. Szeretnéd - megoldani egy másodfokú egyenlet részletesen a szabály fent; akar - csak írja le az a (4), és arra használja, hogy a szükséges következtetéseket.
5. példa az egyenlet megoldásához:
A megoldás, a) Persze, akkor az (4) vagy (3), tekintettel arra, hogy ebben az esetben, de miért manipulálni frakciók egyszerű és ami a legfontosabb, kellemes foglalkozni egész? Nézzük megszabadulnunk a nevezők. Ehhez szorozza mindkét oldalról 12 m. E. A legkisebb közös nevező az egyenlet együtthatóit alkalmazottak. megkapjuk
a 8x 2 + 10x - 7 = 0.
Most használjuk a (4) képletű
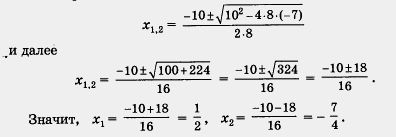
b) Ismét van egy egyenlet frakcionált együtthatók: a = 3, b = - 0,2, c = 2,77. Megszorozzuk mindkét oldalán 100, megkapjuk az egyenlet egész együtthatós:
300x 2 - 20x + 277 = 0.
Ezután használjuk a (4) képlet:
Egyszerű becslés azt mutatja, hogy a diszkrimináns (radikális kifejezés) - negatív szám. Tehát az egyenletnek nincs gyökere.
6. példa egyenlet megoldásához
Határozat. Itt, ellentétben az előző példában, célszerű működtetni a szabály alapján, ahelyett, kondenzált, amelyet a képlet (4).
Van egy = 5, b = -. c = 1, D = b 2 - 4ac = (-) május 02-04 • • 1 = 60-20 = 40. Mivel a D> 0, akkor a másodfokú egyenlet két gyökerei amely kikéri képletek (3)
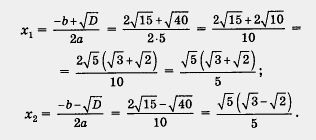
7. példa az egyenlet megoldásához
x 2 - (2p + 1) x + (p 2 + p 2) = 0
Határozat. Ez egy másodfokú egyenlet eltér a fenti még mindig másodfokú egyenlet szolgáló tényezők nem konkrét számokat és szó kifejezéseket. Ezek az egyenletek nevezzük egyenletek együtthatói alfabetikus vagy egyenletek paraméterekkel. Ebben az esetben a paraméter (levél) p része a második együttható és konstans egyenlet.
Találunk a diszkrimináns:
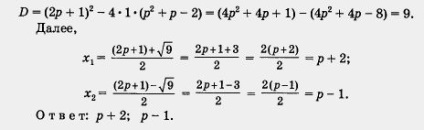
8. példa egyenlet megoldásához Px 2 + (1 - p) X - 1 = 0.
Határozat. Ez is az egyenlet egy p paraméterrel, de, ellentétben az előző példában, azt nem lehet azonnal megoldani a képletek (4) vagy (3). Az a tény, hogy ezek a képletek alkalmazandók másodfokú egyenletek, valamint az adott egyenlet mi nem tud mondani. Sőt, mi lenne, ha p = 0? majd
egyenlet 0 • x 2 + (1-0) x- 1 = 0, azaz x - .. 1 = 0, ami azt jelenti, az x = 1 Most pedig, ha pontosan tudja, mit. lehetőség van arra, hogy alkalmazzák a képlet gyökerei a másodfokú egyenlet: