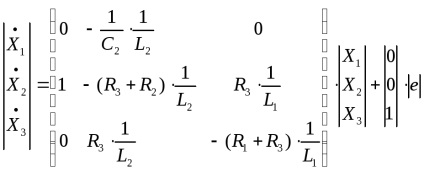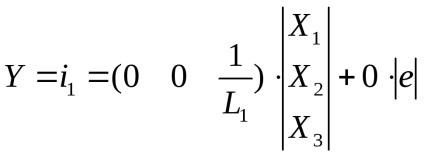Alakítása szűrő és az egyenértékű rendszer
A formázó szűrő - lineáris idő-invariáns rendszer, amely, amikor a bemeneti jel, mint egy fehér zaj, generálja a kimenet előre meghatározott statisztikai paraméterek X (t) véletlenszerű folyamat.
használja a (17) egyenletben meghatározására az átviteli függvény a alakítására szűrő:
.
lövés
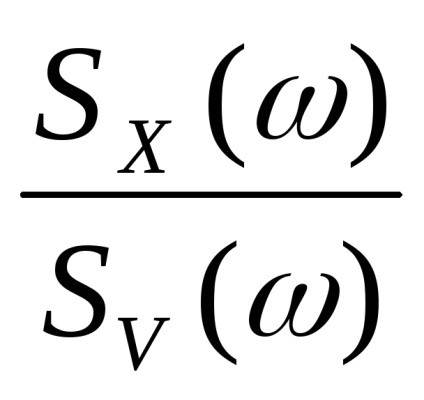
Így, a frekvencia jellemzőit a modul négyzet úgy reprezentálható, mint:
,
ahol
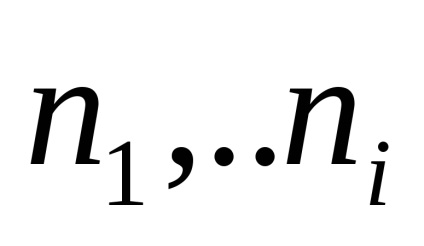
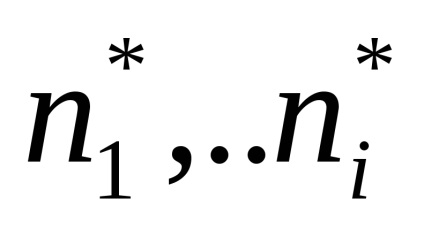

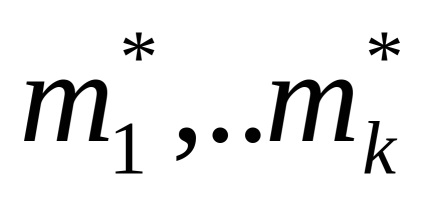
Észrevette, hogy a gyökerek a páronkénti komplex konjugált (azaz,
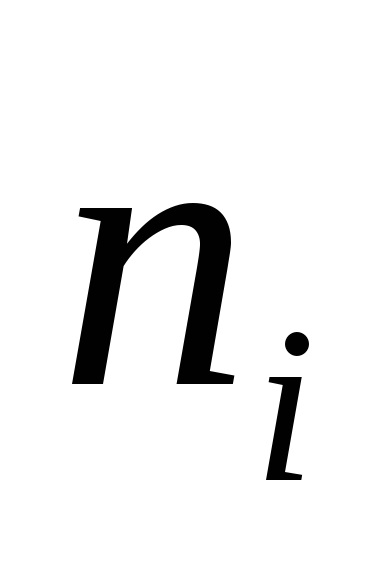
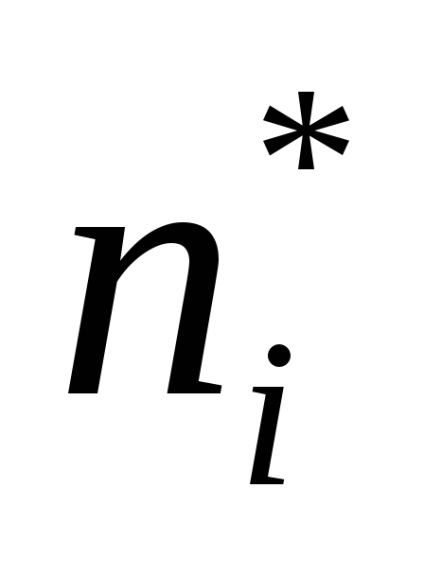
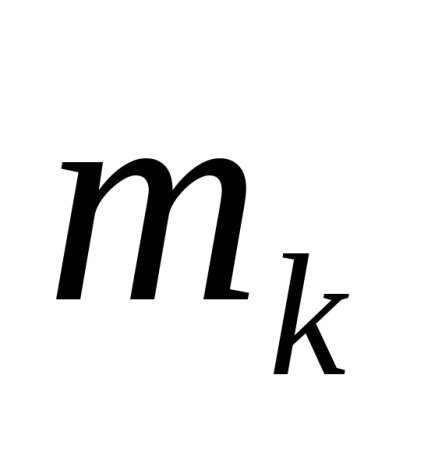
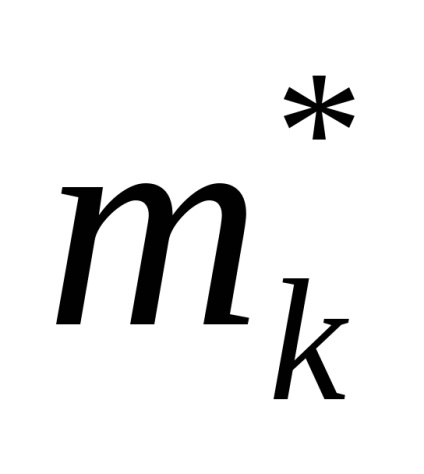
,
.
Így, a kifejezés a kialakulását a alakítására szűrő átviteli függvény
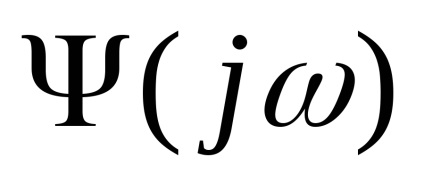
Korrelációs függvény, a spektrális sűrűség egy stacionárius folyamat, a jellemzői a fehér zaj
Stacionárius folyamat - véletlenszerű folyamat megváltoztatása nélkül annak jellemzői idővel és az összes n-dimenziós valószínűségi eloszlásfüggvény nem változik attól függően, változások a kezdési időpont.
Álló korrelációs függvény - véletlenszerű funkció állandó várakozás és korrelációs együttható, attól függően, hogy a különbség az érveket.
.
A spektrális sűrűsége stacionárius sztochasztikus folyamat X (t) - a frekvencia függvényében jellemző spektrális összetételét és a folyamat határozza meg a kifejezést:
A kapcsolat a spektrális sűrűség és a korrelációs függvény:
.
Fehér zaj - stacionárius folyamat állandó spektrális sűrűsége.
.
Véletlenszerűen fehér zaj folyamat, például mindig nincs kapcsolat a korábbi és a későbbi végrehajtását. Ebben a tekintetben a korrelációs függvény fehér zaj:
.
A fehér zaj korrelációs függvény belül const egy δ-funkció - néhány momentum:
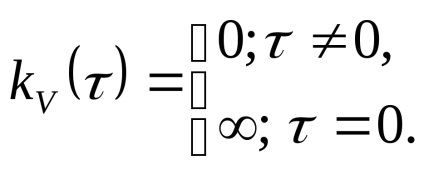
Fehér zaj - stacionárius folyamat, amely rész nem korrelált valószínűségi változók végtelen variancia:
.
Különböztesse intenzitása fehér zaj, amely esetben azt úgy kell kezelni, mint egy nem-stacionárius véletlenszerű folyamat:
,
ahol
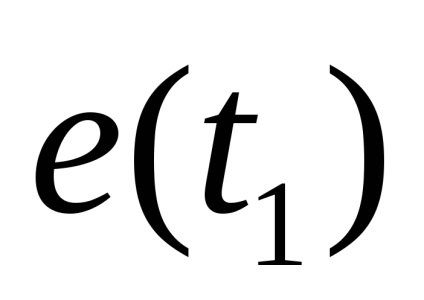
A matematikai modell egy elektromos áramkör
Tekintsük a példát egy matematikai modell egy állapottér egy ellenőrző objektumot, képviseli formájában egy elektromos áramkört (ábra. 3.)
3. ábra. Sematikus ábrája a vezérlő objektum
A vezérlő objektum meg van adva, mint egy elektromos áramkört az átmenet a matematikai leírását az objektum által rögzített második törvénye Kirchhoff egyenlet minden körre. És, hogy megtalálja a rendszert leíró egyenletek vayuschuyu-vezérlő objektum módszerével hurokáramok. Mivel a kimeneti áram értéke használható fel az első kör i1.
Hogy megy a matematikai objektum leírását, írunk a második Kirchhoff törvény egyenletei minden körben, és segítenek megtalálni a rendszert leíró egyenletek vayuschuyu-vezérlő objektum módszerével hurokáramok. A mi esetünkben:
A kezdeti egyenletrendszert kell megszabadulni minden integrálok differenciálásával egyenlet.
Megszabadulni az integrál az utolsó egyenletet:
Az eljárás feltételes integrációhoz adja fiktív változás fajta, azonos elemet vett az egyenleteket, de egy vagy több nagyságrenddel kisebb.
A mi esetünkben, a feltételes integrációs módszer adja hamis változások természetben, az egyenlő elemek tekintetében a következő egyenlet (22) a sorrend alábbi 1. és 2., valamint az első egyenlet (21).
Ez az idő származékok dummy változók, és alkalmazása az előző egyenlőséget kifejező függését az áramlatok és bábuk.
Mert ebben az esetben:
Tól (23) (és adott esetben (21)) áramok vannak kifejezve úgy, hogy azok csak attól függ bábuk.
Tól (23) kifejezés az átfolyó áram a dummy változók felírható:
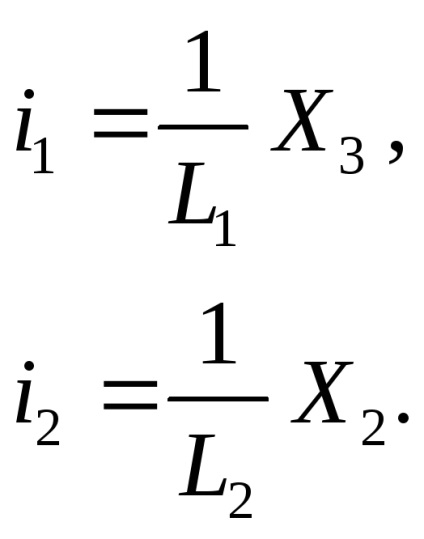
A kifejezést kapjuk áramok vannak szubsztituálva (24) rendszer, és egészítik ki a kifejezést a kimeneti érték eredményeként kapott.
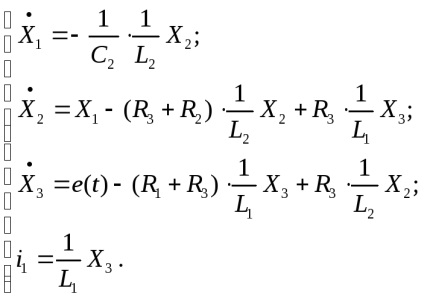
Szerint kapott egyenletrendszert és az egyenlet a kimeneti változó ellenőrzött objektum tárolt matematikai modell a normál odds Cauchy-me:
- Egyenlet a szállított mennyiség az objektum.
ahol A, B, C, D - mátrix, X - mátrixa belső változók, U - mátrix bemeneti változók, ebben az esetben U - EDS.
Ebben az esetben a mátrix fog kinézni:
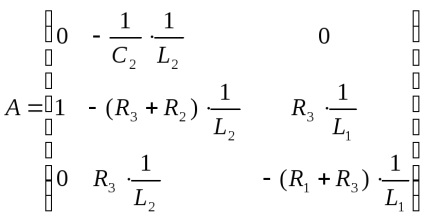
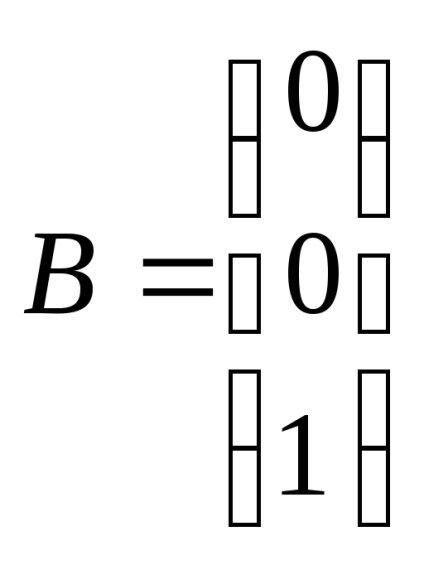
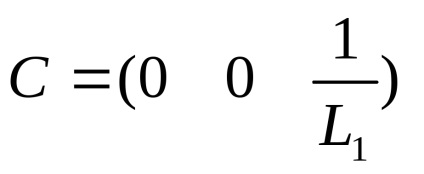
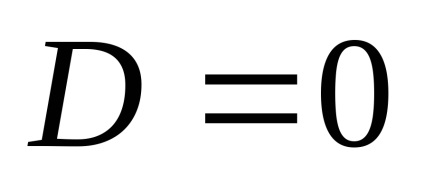
Kapunk egy matematikai modell állapot-tér: