Szekcionált prizma - prizma - Geometria - Geometria - Matematika
II. szeterometria
2. A keresztmetszetek a prizma.
Tekintsünk néhány egyszerű keresztmetszetét a prizma.
A keresztmetszet a prizma, amely áthalad a két oldalsó széle nem tartozó egyik alapja, az úgynevezett átlós részének.
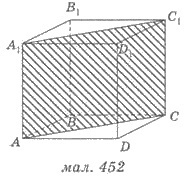
Ábra 452 AA 1 C 1 - átlós keresztmetszete egyenes hasáb. Ez a keresztmetszet egy téglalap, egyik oldalán - az AC átló bázis és a másik - az oldalsó szélén UE 1. A ferde prizma átlós részének egy paralelogramma.
Gyakran a problémák nem csak azért szükséges, hogy építsenek egy keresztmetszet, hanem találni egy olyan területen, vagy kerületi, vagy egy részén más célra.
1. példa Egy egyenes hasáb alapján rombuszt egy oldala 4 cm, és hegyesszög 60 °. Find a terület az átlós prizma szakasz, amelynek egyik oldalán van a nagy diagonális a rombusz, ha az oldalsó széle a prizma egyenlő 2 cm.
Megoldásokat. 1) Legyen ABCDA 1 B 1 C 1 D 1 - prizma, amelynek alapja egy rombusz ABCD. AB = 8 cm, A = 60 °, AS - nagy átlója egy rombusz (ábra 452.). Ezután ACC 1 A1 - átlós részének a területet szeretné megtalálni. CC = 1 cm 2 (a feltétellel).
3) Δ ADC és a koszinusz tétel:
Gyakran problémák tekintetében a prizma keresztmetszetű keresztül húzódó oldalán a prizma bázis és amelyek keresztezik az oldalsó szélei a prizma.
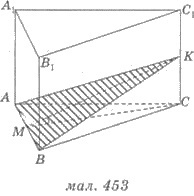
2. példa Az alapja sorban a prizma egy egyenlő oldalú háromszög, amelynek oldalán egyenlő 2 cm. Egy oldalán a háromszög tartott részén, amely szöget a 30 ° a bázissal sík és metszi a oldaléle annak közepén. Keresse meg a hossza a pereme a prizmát.
Megoldásokat. 1) Legyen B1 ABCA1 C 1 - háromszögű hasáb, amelynek alapja - ABC egyenlő szárú háromszög, AB = 2 cm (lásd ábra 453) ..
2) Miután az AB oldal bázis háromszög lefolytatott AVC részén, ahol K - 1 felezőpontja SS.
3) Döntetlen a medián SM ABC háromszög, ami szintén a magasság a háromszöget.
4) Mivel a CM AB és CM CM egy vetülete a ABC síkot a tétel három merőlegesek: CM AB.
Ezután CCM - a bezárt szög a sík keresztmetszete a bázis. A CCM feltétel = 30 °.
6) Mivel a K - 1 felezőpontja SS SS = 1 2KS ∙ = 1 2 = 2 (cm).