Átlós prizma szakasz - kép 26266-14
Az átlós szakasz >>
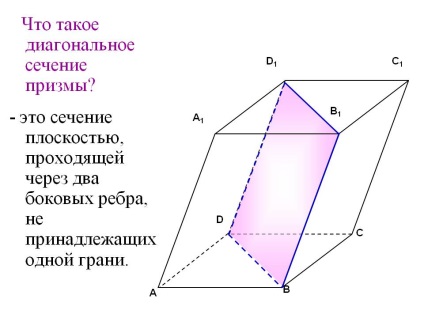
Mi az átlós rész a prizma? - egy szakaszt áthaladó sík, két oldalsó széle nem tartozó egyik oldalán. D1. C1. B1. A1. D. C. B. A.
Kép 14 bemutatásának „geometriai test prizma” egy geometria lecke „Prism”
Méret: 960 x 720 pixel, formátuma: jpg. Töltse le a képet a geometria leckét, kattintson a képre a jobb egérgombbal, és kattintson a „Kép mentése más néven. ”. A képek megjelenítésére az osztályban, akkor is letölthető egy ingyenes előadást tart „geometriai test prizma.ppt” teljesen az összes kép a zip-archívum. fájlméret - 265 KB.
„Ábra prizma” - szabályos hasáb. Belátjuk a tétel az első háromszög prizma. Ferde és prizma. Elmozdulás ferde hasáb. Típusai prizmák. A terület a palástfelület a prizma. Prism. Összfelülete a prizma. Meghatározása a prizma. Most bebizonyítjuk, a tétel egy tetszőleges prizma.
„A tulajdonságok a prizma” - általános képletű három koszinuszok. Konvex poliéder. A háromszög alakú prizma. Sine tétel háromszög szöge. Koszinusz tétel háromszög szöge. Prism nevezzük poliéder. Körül néhány fajta prizmák mindig leírják a hatálya alá. Megfogalmazott feltételek egy egyenes hasáb. Henger. A keresztmetszet a henger.
„A koncepció egy prizma” - szabályos hasáb. Prism találkozott az életben. Bizonyítás. A terület a palástfelület a prizma. Összfelülete a prizma. Prism. Polygon. Elmozdulás ferde hasáb. A keresztmetszet a prizma. Prism. Meghatározása a prizma. Ferde és prizma. Háromszögű hasáb. Típusai prizmák.
„A koncepció egy poliéder prizma” - jobb keresztmetszete a prizmát. Bizonyítás. A keresztmetszet a prizma. Adott: Az alsó oldala szabályos háromszögű hasáb 8 cm, az oldalsó borda - 6 cm. Következmény. Megkülönböztetni háromszög prizma, négyszög, ötszög, stb számától függően bázis csomópontok. Az egyenes hasáb oldala nézzen - téglalapok.
„A prizma geometria” - A „prizma” görög eredetű, és szó szerint azt jelenti „cut-off” (a szervezetben). Parallelepipedonok, prizmák lehet egyenes és ferde. Megoldás: Legyen CM merőleges levont pont C BC1D síkra. Prism az ókorban. Keresse az oldalán az alap a prizmát. A magasság az egyenes háromszögű hasáb ABCA1B2C3 egyenlő 10.
Csak a „Prism” 10 előadások