Tudd Intuíció, előadás, numerikus integrálással
Kivonat: A legegyszerűbb interpoláció kvadratúra formula - téglalapok, trapéz, Simpson. Ahhoz, hogy megbecsüljük a tényleges hiba képletek jellemzően Runge. Ez ad egy ötletet a Gauss kvadratúra képletek. Kiszámításához használt módszereket többdimenziós integrálok.
Ez az előadás fogja vizsgálni a problémát a numerikus integrálást. Képletek numerikus integrálása egyváltozós függvényeket nevezzük kvadratúra képletek. A feladat számítási közelíti a határozott integrál (a szegmens vagy egy többdimenziós régió) valójában két részre független al-feladatokat. Először - táblázatos előre meghatározott integrációs funkció (beszerezhető például során laboratóriumi kísérlet). Ebben az esetben az a priori információt simaságát az integrandus nem nagyon korlátozott lehetőségek a választott integrációs helyek. Ezt a problémát, leghatékonyabbnak kvadratúra- képletek az interpoláció típusa és zárja Runge hibabecslése.
A második probléma - count értéke a határozott integrál ismert funkciót. Így a legtöbb fogyasztó működése szempontjából computing - száma a függvény értékét. Kívánatos, hogy össze egy numerikus módszer, így a lehető legnagyobb pontossággal a legkisebb számú számítási csomópontok és a kiválasztott kvadratúra képletek teljesen a kezében egy számológép. Ebben az esetben ez lesz a leghatékonyabb típusú Gauss kvadratúra képletek.
7.1. Quadrature képletű interpolációs típusú (Formula Newton - Cotes)
A legegyszerűbb kvadratúra képletű (a képlet numerikus integrálással) állíthatjuk elő a következők szerint. Tegyük fel, hogy szeretnénk számítani a szerves
Tegyük fel, hogy F (t) a szegmens [a, b] nem változik (). Akkor, ha
megkapjuk képletű téglalapok középpontja
Természetesen a állandói a fenti képlet pontos - mondjuk épült kvadratúra- formula pontos lesz a polinomot lehet 0. Könnyen bizonyítani, hogy a tápszer és a középpont a téglalap nem ad pontos értéket abban az esetben egy lineáris függvény. Minden más funkciónál a ez a képlet tekinthető hozzávetőleges.
Feltételezve, hogy az f (t) intervallumban az integráció [a, b] elegendően közel lineárisak, lehetőség van helyettesíteni a közelítő értéke az integrál i terület egy trapéz, amelynek magassága (b - a) és a bázisok F (a) és f (b). Ezután, a képlet a trapéz
Általában, a kvadratúra képletek integrálásával kaptunk interpolációs polinom közelítő integrandust. Család kvadratúra képletek így kapott nevezik interpolációs típusú formulák (Formula Newton - Cotes).
Bemutatjuk a szegmens rács integráció, határozza meg a függvény értékei a rácspontok. A csomópont neve a továbbiakban csomópontok képletű kvadratúra (vagy kvadratúra). Tegyük fel, mint az a probléma a interpoláció, van egy csomópontok halmaza, és hagyja, terített asztal szegmens [tk. tk + 1] a továbbiakban néha lesz az úgynevezett elemi intervallumot.
Cserélje ki az integrandus az interpolációs polinom Lagrange formában. Azt feltételezzük, hogy
Nézzük meg néhány speciális esetet.
Trapéz szabály. Az intervallum [tk. tk + 1] felváltja a integrandust interpolációs polinom első fokú:
majd végző integráció elemi intervallumot kapunk egy közelítő értéke integrál [tk. tk + 1]:
Miután összegzése integrálok az egész elemi időközönként [tk. tk + 1] megkapjuk trapéz szabály az [a, b]:
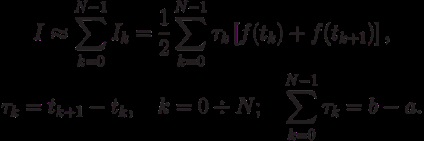
Egy egyenletes rács (rács egyenlő távolságra lévő csomópontok) a kapott általános képletű válik