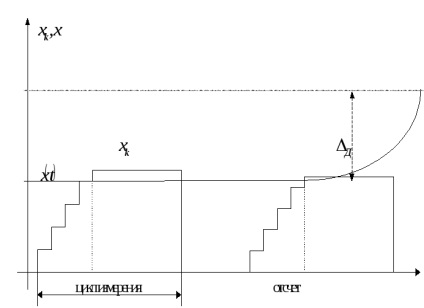
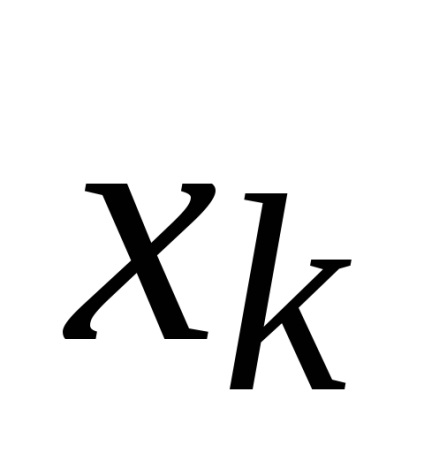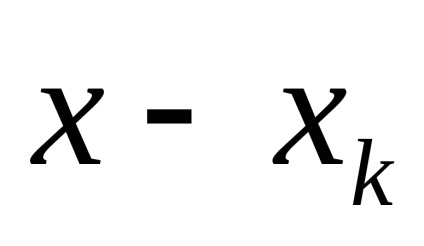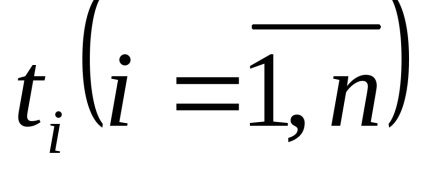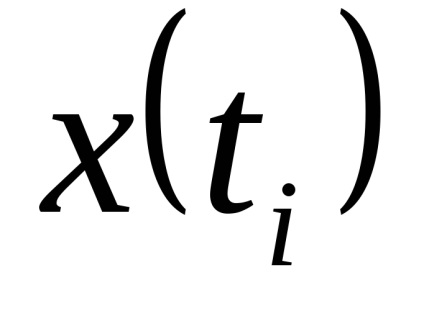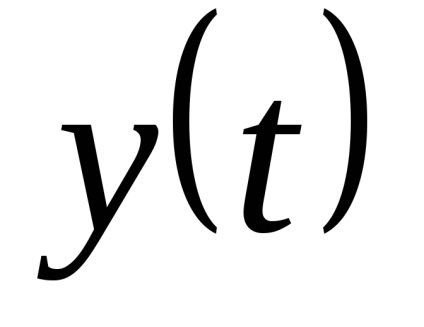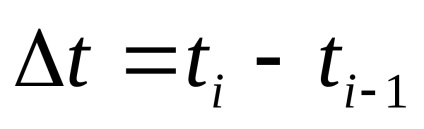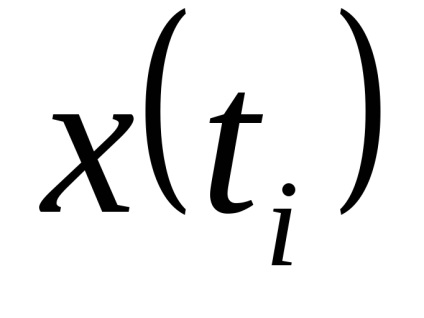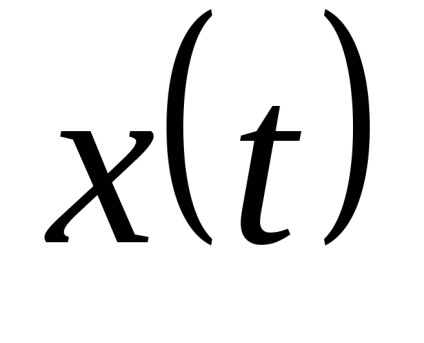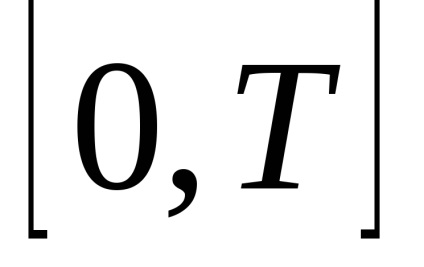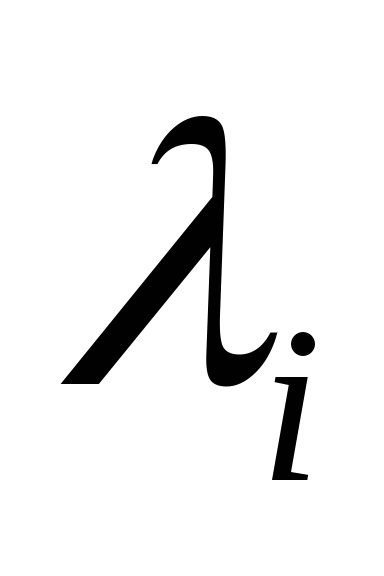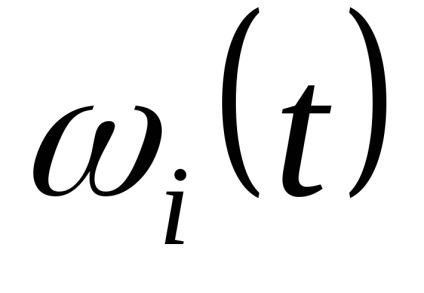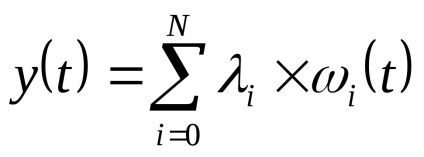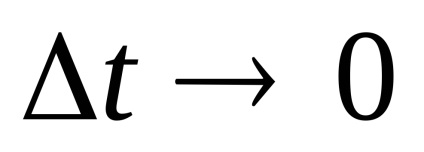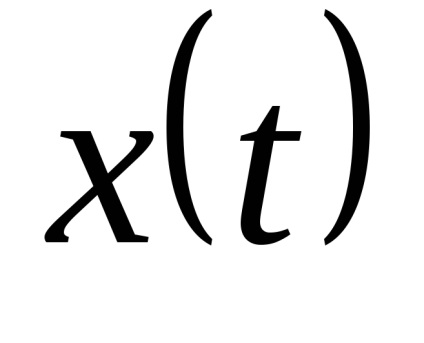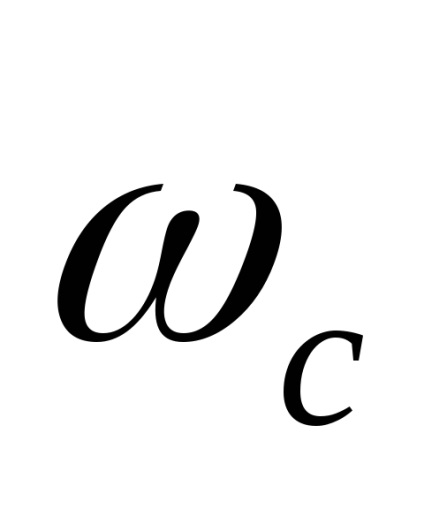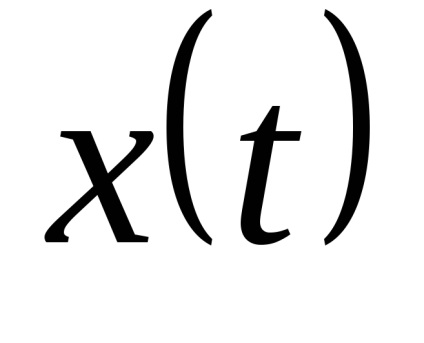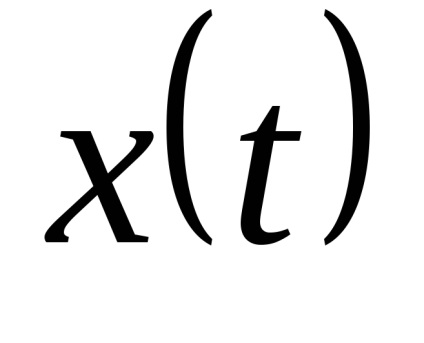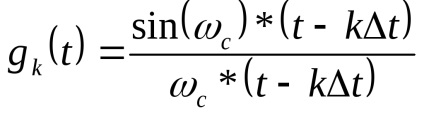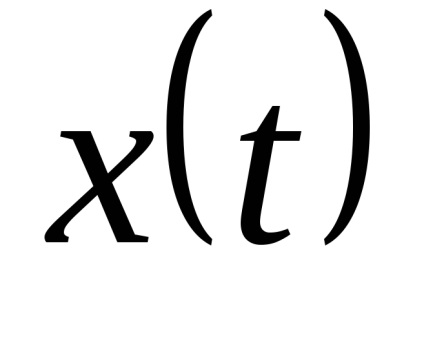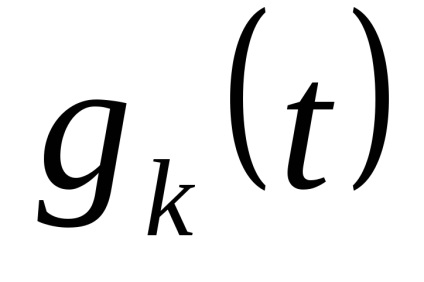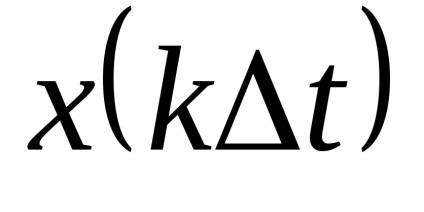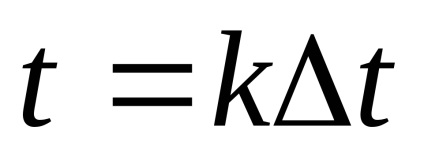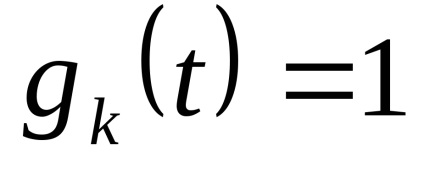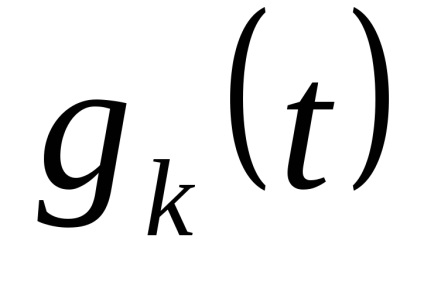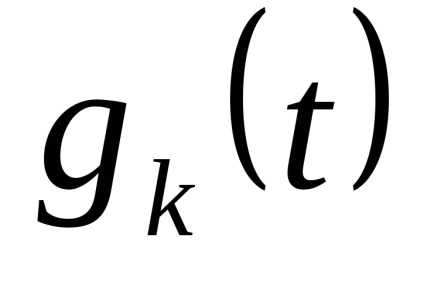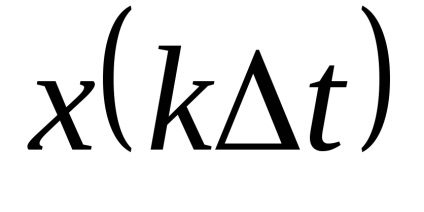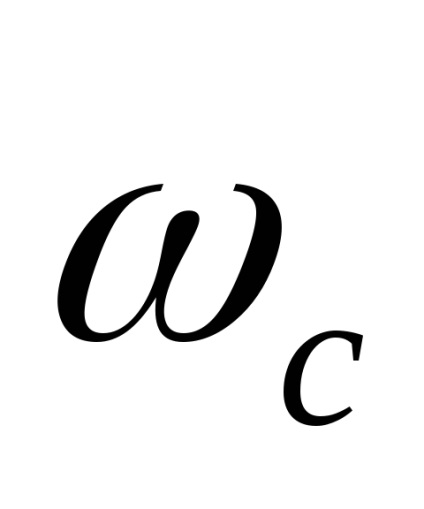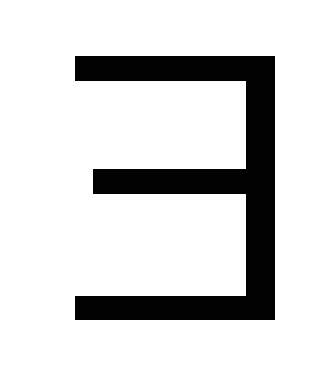Bérleti jog x ih véletlen. Mivel a kvantálási szinteket a legjobb, hogy a közepén a partíció szegmensben. (Itt!)
Attól függően, hogy a módszer a CIP konverziós eszközök vannak osztva a közvetlen és ekvilibrációs konverzió.
A DRC nem közvetlen átalakítása teljes visszajelzést. Nekik van egy nagy teljesítményű, de a pontosság magas csak nagy pontosságú minden átalakítók.
CIP egyensúlyba átalakítás tartozó általános visszajelzést. visszajelzést DAC átalakító diszkrét kimeneti jel egy kompenzáló értéket xk a fizikai természetét egy mért érték x (t). DAC készült elemek nagy pontosságot és stabilitást.
Vannak eszközök telepítésére és Egyengetésért.
Az első szakaszban értéke a kiegyenlítő értékek
minden egyes mérési ciklusban nullától állapotok egyenlő a kvantálási lépésben. Amikor elérte az egyenlőség kiegyensúlyozó folyamat megszakad, és a mérési eredmény van rögzítve, ahány kvantálási lépés a kompenzáló értéket. Üzemóra többnyire a ciklus végén.
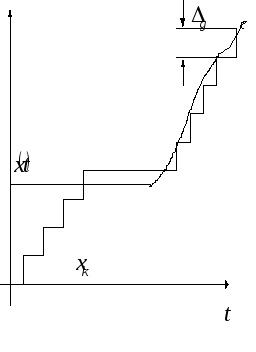
Van egy dinamikus hiba d.
az
Egyengetésért eszközök kompenzálja a nagysága nem tér vissza teljesen, de állandó marad. Ha x követjük a
nem haladja meg a kvantálási lépés értékét. Számlálás vagy előállított idején egyensúlyba vagy külső parancsokat. Nehezebb technikailag.
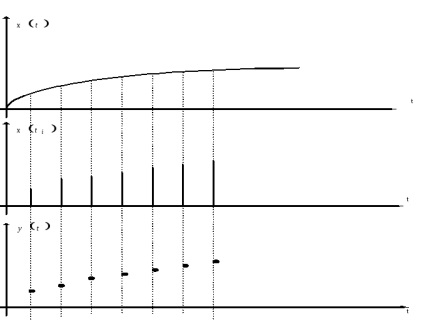
6.3. Diszkrét idejű mintavételezés és helyreállítási folytonos függvények.
Számos módja van, hogy a mintavétel.
Az átmenet a folytonos idejű funkcióját a diszkrét idejű funkció is ellátható mintákat véve a funkció bizonyos diszkrét időpontokban
. minták
Vissza tudja állítani más funkció (ismeretlen)
, reprodukálja az eredeti egy adott pontossággal. Amennyiben a mintavételi idő az egyik legfontosabb a választás kérdése a mintavételi lépéseket:
.
Van egy optimális mintavételi intervallumot, amely biztosítja a visszaálljon az eredeti funkciót egy adott pontossággal egy minimális számú mintát
véges időintervallum.
folytonos függvény
A megfigyelési intervallum
Úgy helyébe véges számú tágulási tényezőjük
a választott rendszer alapfunkciók
Az előnye ennek a rendszernek.
Abból lehet kiindulni, hogy pontos helyreállítását az eredeti folytonos függvény az idő csak akkor lehetséges, ha
. Azonban van egy széles osztálya folyamatok, amelyekre a pontos rekonstrukció lehetséges véges értéke a mintavételezési lépés. Ebbe az osztályba tartozik a jelek korlátozott tartományban.
6.3.1. Nyquist-tétel.
Ha egy folytonos függvény
Ez megfelel a Dirichlet körülmények között (korlátozott, db-bölcs folytonos, és van egy véges számú szélsőérték), és a tartomány korlátozott egy bizonyos frekvenciáig
(Határfrekvencia), létezik egy minimális időköz
minták között, ahol ez lehetséges, hogy pontosan visszaállítani a funkció a mintában
diszkrét leolvasás. Ez a maximális intervallum:
Alapján tétel a lehetőségét, hogy a bővítés
egy sorban:
funktsiya mintákat (6.7)
Ie függvény
tudjuk bővíteni a rendszert alapfunkciók
. És razlozheniyaznacheniya együtthatók
diszkrét alkalommal.
a
max érték
funkciók
merőleges végtelen nagy időintervallumot.
A gyakorlati értéke a függvény Kotelnikov sorozat az, hogy a kommunikációs csatorna nem sugározzák formájában ismert minta funkció
, de csak átvitt rács funkció
.
Abból a szempontból gyakorlati megvalósítása teljes funkció számít megfelel a változás az időben kimeneti feszültsége az ideális aluláteresztő szűrő halad minden frekvencián egyaránt 0-tól
, alkalmazása során a bemenetére
impulsa.
Reálértéken pontos helyreállítása lehetetlen annak a ténynek köszönhető, hogy a feltételek nem teljesülnek Nyquist-tétel.
Az igazi funkciója
véges időintervallum, így a spektrumok végtelenek.
Kapcsolódó cikkek