Tudd Intuíció, előadás, rekurzió és a fák
dinamikus programozási
A fő jellemzője az algoritmus típusát „oszd meg és uralkodj”, 5.2 fejezet tárgyalja - a probléma felosztást független részfeladatokra. Ha a részfeladatok nem függetlenek, a helyzet bonyolult, különösen azért, mert a közvetlen rekurzív végrehajtását még a legegyszerűbb algoritmus az ilyen típusú megkövetelheti elfogadhatatlan mennyiségű időt. Ez a rész ismerteti a szisztematikus megközelítés, amely elkerüli ezt a kockázatot bizonyos esetekben.
Például a szoftver 5.10 - közvetlen rekurzív végrehajtását rekurzív sorozat meghatározó Fibonacci-számok (lásd „elemi adatok szerkezetét.”). Ne használja ezt a programot - ez nagyon hatékony. Sőt, a szám a rekurzív hívások kiszámításához egyenlő FN FN + 1. De FN megközelítőleg megegyezik az f N. ahol f „1,618 -.... aránya az aranymetszés Meglepő, de a program 5.10-szor ezt az elemi számítás által meghatározott exponenciális függés ábra 5.14, amely azt mutatja, a rekurzív hívások egy kis példa, egyértelműen kimutatható a szükséges mennyiségének újbóli számításokat.
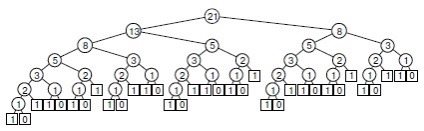
Ábra. 5.14. A szerkezet egy rekurzív algoritmus kiszámítja a Fibonacci
A rekurzív számítási áramkört F8 standard rekurzív algoritmus lehet tekinteni, mint a rekurzió átfedő részfeladatok vezethet exponenciális növekedéséhez költségeket. Ebben az esetben a második rekurzív hívás figyelmen kívül hagyja az elvégzett számítás során az első hívást, ami jelentős újbóli számítástechnika, hiszen a hatás exponenciálisan növekszik. A rekurzív hívások kiszámításához F6 = 8 (a jobb oldali részfa gyökerének és a bal oldali részfa gyökerének a bal részfa) az alábbiakban mutatjuk be.

Ezzel szemben, a szokásos sor, akkor könnyen kiszámítható az első N Fibonacci számok idő arányos N:
A számok exponenciálisan növekszik, így a tömb nem kell nagynak lennie; így például, F45 = 1836311903 - legmagasabb Fibonacci szám, amely képviseli a 32-bites egész, így elegendő használni egy sor 46 elemek.
Ez a megközelítés biztosítja a közvetlen előállítási módjának numerikus megoldások minden rekurzív sorozat. Abban az esetben, Fibonacci-számok lehet tekinteni akkor is, anélkül, hogy a tömb, és kizárólag az utóbbi két érték (lásd Exercise 5.37.); azonban sok más esetben gyakori rekurzív sorozat (lásd. például testedzés 5,40) szükséges tárolására a tömb összes ismert értékek.
Program 5.10. Fibonacci-számok (rekurzív végrehajtás)
Ez az eszköz úgy néz ki, kompakt és elegáns, de nem alkalmazható a gyakorlatban, mert a számítási idő exponenciálisan függ FN N. Az idő számításánál FN + 1 f „1,6-szer hosszabb számítás FN. Például, mivel f 9> 60, ha a számítógép kiszámítja a szükséges Fn körülbelül egy másodpercig, hogy kiszámolja 9 FN + igényel több mint egy perc alatt, és kiszámításának FN + 18 - több mint egy óra.
A rekurzív sorozat - egy rekurzív függvény egész értékek. Az érvek adott az előző bekezdésben, azt sugallják, hogy az ilyen funkciót ki lehet számítani kiszámításakor az értékeket is, kezdve a legkisebb, és minden egyes lépésnél, az előzőleg kiszámított értékek kiszámításához az aktuális értéket. Ezt a technikát nevezik emelkedő dinamikus programozás (alsó le- dinamikus programozás). Ez vonatkozik minden rekurzív számítási, feltéve, hogy ez lehetséges, hogy tárolja az összes a korábban számított értékeket. Ilyen algoritmus fejlesztési technikát már sikeresen alkalmazzák széles körű feladatokat. Tehát figyelni ezt az egyszerű technológia, amely megváltoztathatja a végrehajtási időt az algoritmus exponenciális lineáris!
Lefelé dinamikus programozás (top fel- gombok valamelyikét dinamikus programozás) - még egyszerű technika, amely lehetővé teszi, hogy automatikusan elvégzi a rekurzív függvények azonos (vagy kisebb) ismétlések számát, mint az upstream dinamikus programozás. Ha ez a program rekurzív (záródáshoz) tárolja az egyes számított érték és s (első kereset) ellenőrzi ezeket az értékeket, hogy elkerüljük újraszámítása ezek közül bármelyik. Program 5.11 - az eredmény a mechanikai 5,10 átalakítási programot, ahol a dinamikus programozási lefelé csökkenteni lehet az átfutási idő lineáris.
Ábra. 5.15 bemutatja a drámai számának csökkenése rekurzív hívások elérni ezeket az egyszerű automatikus váltás. Előfordul, hogy a lefelé irányuló dinamikus programozás is nevezik memoization (memoization).
Mint egy bonyolultabb példát, úgy a probléma a hátizsákot: a tolvaj kirabolt egy széf tartja N típusú objektumok különböző nagyságú és értékű, de csak egy kis hátizsák kapacitás M, amelyre képes hordozni a zsákmány. A kihívás az, hogy meghatározza a kombinációját tartalmazzák, hogy a tolvaj kell hozni egy hátizsák, a teljes értéke az ellopott volt a legnagyobb.
Program 5.11. Fibonacci-számok (dinamikus programozás)
Tárolása A kiszámított értékeket egy statikus tömb (elemek, amelyekben a C ++ inicializálva 0) lehetővé teszi kifejezetten kizárják minden ismétlődő számítások. Ez a program kiszámolja Fn időben arányos N, ami lényegesen eltér a időt 0 (f N), amely szükséges a számítási program 5.10.
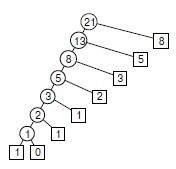
Ábra. 5.15. Alkalmazása a lefelé dinamikus programozás kiszámolni Fibonacci
E rendszerben a rekurzív hívások kiszámításához F 8 lefelé dinamikus programozási, lehet tekinteni, mint a megőrzése számított érték csökkenti a költségeket az exponenciális (lásd. Ábra. 5.14) lineáris.
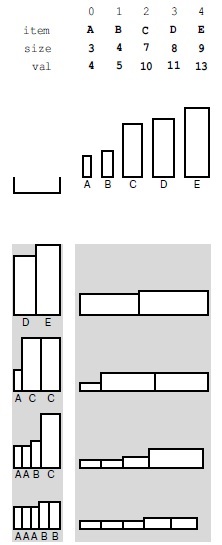
Ábra. 5.16. Példa hátizsák problémával
A bemenő adatok hátizsák problémával (fent) a háti kapacitás és néhány tárgy különböző méretű (által képviselt értékek a vízszintes tengelyen) és érték (value függőleges tengely). Ez az ábra azt mutatja, a négy különböző módon a töltés a hátizsákot, amelynek mérete megegyezik a 17; Két ilyen módszer, hogy a maximális teljes értéke egyenlő 24.
Például, jelenlétében típusú objektumok ábrán látható. 5.16. Tolvaj, amely egy hátizsák amelynek mérete 17, lehet, hogy csak öt (de nem hat) veti alá a teljes érték 20, vagy tételeket D és E a teljes érték 24 vagy az egyik a több más kombinációk. A cél -, hogy megtaláljuk egy hatékony algoritmust az optimális megoldást adott objektum és a háti kapacitást.
Megoldása a hátizsákot egy fontos probléma a sok alkalmazás. Például a közlekedési vállalat lehet szükség, hogy meghatározzuk a legjobb módja, hogy teher egy kamion vagy szállító repülőgép. Ezekben az alkalmazásokban találkozhatunk és egyéb változatai ezt a problémát: például korlátozott lehet az elemek száma az egyes típusú, vagy lehet elérni két teherautó. Sok ilyen lehetőség lehet oldani ugyanazt a megközelítést, amelyet az alábbiakban tárgyalt a megoldást csak megfogalmazott alapvető feladata, de vannak sokkal kifinomultabb lehetőségeket. Van egy finom vonal között megoldható és megoldhatatlan problémák az ilyen típusú, de ez lesz szó 8. rész.
A rekurzív megoldás a hátizsák problémával minden alkalommal, amikor kiválaszt egy tárgyat, azt feltételezzük, hogy tudjuk (rekurzív), hogy meghatározzák a legjobb módja annak, hogy töltse ki a fennmaradó hely a hátizsákot. Ha az összeg háti sapka, az egyes elemekhez i határozza meg összértéke elemeket, amelyek vinni a pályáról, üzembe i-edik eleme az hátizsákot optimális csomagolására a maradék elemek. Ez az optimális csomagolás - csomagolási definiált (vagy meg kell határozni) kisebb térfogatra háti sapka -items [i] .size. Ez az elvet követi, hogy a legjobb döntéseket a jövőben felülvizsgálatára nincs szükség. Ha a beállítás optimálisan csomagolja a hátizsák kisebb méretű, ezek a feladatok nem igényelnek ismételt vizsgálatot, tekintet nélkül a következő elemeket.
Program 5.12 - közvetlen rekurzív megoldást, amely alapján a fenti érvelést. A program nem vonatkozik a valós problémák megoldására, mert a nagy mennyiségű ismétlődő -ez számítás (lásd. Ábra. 5,17), míg az oldat kapcsolódó elemek száma exponenciálisan. De lehetséges, hogy automatikusan aktiválja a lefelé dinamikus programozás, hogy megoldja a problémát -, és hogy a program 5.13. Mint korábban, ez a technika kizár minden ismétlődő számítások (lásd. Ábra. 5,18).
Program 5.12. Hátizsák problémával (rekurzív végrehajtás)
Mint abban az esetben a rekurzív számítása Fibonacci-számok, ne használja ezt a programot, mert annak végrehajtása lesz szükség exponenciális időt, és ezért nem lehet tudni, hogy oldatot kapjunk, még egy kis probléma. Azonban, a program egy kompakt megoldást, amely könnyen lehet javítani (ld. 5.13 programot). Feltételezzük, hogy az elemek szerkezetek mérete és a költségek, melyek meghatározása a
és egy sor N pont típusú elemek. Az egyes lehetséges elemek számítjuk (rekurzívan), a maximális érték, amely előállítható beépítésével az elem a mintában, majd válassza ki a legmagasabb az összes értéket.
Program 5.13. Hátizsák problémával (dinamikus programozás)
Ez a mechanikai módosítás programot 5,12 csökkenti az átfutási idő exponenciális lineáris. Mi csak tartani az összes számított értékei a funkciót, majd végrehajtása helyett rekurzív hívásokat, válasszuk a tárolt értékeket mikor van szükség (egy speciális flag képviseletére ismeretlen értékek). Az index tartjuk azonban, ha szükséges, bármikor visszaállíthatja a tartalmát a háti kiszámítása után: itemKnown [M] egy hátizsákot, egyéb tartalom egybeesik az optimális csomagolási mérete háti M -itemKnown [M]. mérete, ezért a hátizsákot van itemKnown [M -items [M] .size] stb
Ábra. 5.17. A rekurzív szerkezetét az algoritmus megoldása hátizsák problémával
Ez a fa struktúráját szemlélteti rekurzív hívások egyszerű rekurzív algoritmus megoldása hátizsák problémával, végre a programban 5.12. A szám minden egyes csomópont jelzi a maradék tér a hátizsákot. A hátránya az algoritmus ugyanaz exponenciális futási a -Ez ismételt nagy térfogatú számítások megoldásához szükséges átfedő részproblémákat, hogy a számítás a Fibonacci számokat (lásd. Ábra. 5.14).
Ábra. 5.18. A módszer alkalmazása csökkenő dinamikus programozási algoritmus végrehajtása a döntést a hátizsák problémával
Akárcsak a számítási Fibonacci természetvédelmi értékek ismert technika csökkenti a költségeket algoritmus exponenciális (lásd. Ábra. 5.17) lineáris.
Dinamikus programozás elve kizárja újra kiszámítani a rekurzív programot, feltéve, hogy lehet tárolni az értékeket érvek kevesebb, mint az érv az aktuális hívást.
Lemma 5.3. Dinamikus programozás csökkenti futási rekurzív függvény nem több, mint a teljes szükséges idő kiszámítása a funkció minden érv, kisebb vagy egyenlő, mint a felhozott érv, azzal a feltétellel, hogy állandó rekurzív hívás költségeit.
Lásd. Legyünk 5.50.
Ami a problémát a hátizsákot a lemma, hogy az átfutási idő arányos a NM. Így a hátizsák problémával egyszerűen megoldható, ha a kapacitás a hátizsákot nem túl nagy; nagyon nagy tartályokba az idő és tárolási követelmények megfizethetetlenül nagy.
Származás dinamikus programozás is alkalmazható a hátizsák problémával. -Ez minden módszer minden esetben, akkor lehet alkalmazni a növekvő programozási módszer, amikor lefelé irányuló programozás csak akkor alkalmazható, ha ez szükséges ahhoz, hogy az értékek kiszámítását a megfelelő sorrendben, hogy minden értéket úgy számították ki, amikor szüksége van rá. Mert funkciók egyetlen egész érv, mint említettük, akkor egyszerűen számítások elvégzésére annak érdekében, érvelés (lásd. Legyünk 5,53), de bonyolultabb rekurzív függvények meghatározására a helyes sorrendben is kihívást jelent.
Például, de nem szükségszerűen korlátozódik a rekurzív funkciót egyetlen egész érv. Ha van egy funkció több érveket egész megoldását kisebb al-feladatokat lehet tárolni többdimenziós tömbök, egy mérés az egyes paraméterek. Más helyzetekben, meg tudod csinálni anélkül, hogy bármelyik egész érvek és használja absztrakt diszkrét megfogalmazása a probléma, amely lehetővé teszi, hogy megtörje a feladat kevésbé komplex. Példák az ilyen problémákat veszi figyelembe részein V - VIII.
Amikor az ismert lefelé irányuló dinamikus programozási értékeket tárolják; Ezek kiszámítása a felfelé dinamikus programozási előre. Általában a top-down dinamikus programozás előnyös emelkedik, amint
- ez egy mechanikus probléma megoldások természetes átalakulás;
- rendelni sub megoldások határozzák meg önmagában;
- Lehet, hogy nem igényel a megoldás minden részfeladatot.
Használó alkalmazások dinamikus programozás, különböző jellegű és térfogata al információt tárolja őket.
Azonban felhívjuk figyelmét a következő fontos pont: dinamikus programozás hatástalanná válik, amikor a lehetséges értékek számát egy függvény, ami szükséges lehet olyan nagy, hogy nem engedhetjük meg magunknak, hogy tartsa őket (egy lefelé programozás) vagy előre kiszámolhatja (egy emelkedő programozás). Például, ha a hátizsák problémával háti térfogata és méretei elemek - 64 bites értékek vagy lebegőpontos értékek már nem lehetséges fenntartani, által az index a tömbben. Ez nem csak egy apró kellemetlenség, ez egy alapvető nehézséget. Ezen feladatok, ez nem ismert, bármilyen elfogadható megoldást; mint látni fogjuk 8. részében, jó okunk van azt hinni, hogy egy hatékony megoldás egyáltalán nem.
Dinamikus programozás - ez az algoritmus fejlesztési technika, amely elsősorban a kihívások, ilyen típusú, amelyet figyelembe kell venni a Parts V - VIII. A legtöbb algoritmusok tárgyalt részek II - IV, egy megvalósítása a módszerek „oszd meg és uralkodj”, hogy a nem-átfedő al-problémák, és figyelni a legtöbb Subquadratic növekedési vagy szublineáris teljesítményt, mint subexponential. Ugyanakkor a csökkenő dinamikus programozás alapvető technika, hogy hatékony implementáció rekurzív algoritmusok, amely jelen van az Arsenal, aki részt vesz a létrehozása és végrehajtása algoritmusok.