Szövetségi Oktatási Ügynökség
Értékesítéséből származó haszon egy termelési egység az első típusú 2 den. u második faj - 3 den. U ..
A feladat az, hogy létrejöjjön egy termelési program kimenete, amely a legjobb megtérülést annak végrehajtását.
A értékesítéséből származó haszon az adatok az egyes típusú termék, tudjuk átalakítani az 1. táblázat 2. táblázat.
Norma erőforrás költségek az áruk
Összes forrás
Gain eladó
EMM alkotják a feladat.
Hagyja, x1 és x2 - mennyiségét az 1. és 2. formák eléréséhez szükséges a maximális profit. Akkor EMM fog kinézni:
X = (x1, x2) - vektor, ahol F (X) → max és korlátok elégedett
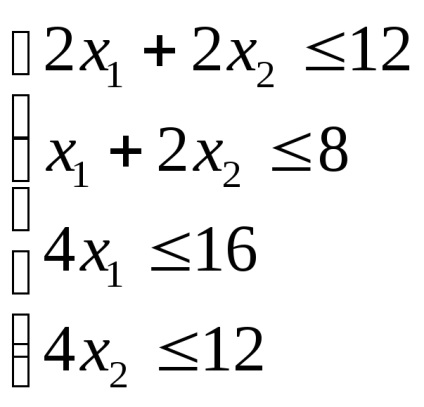
Mi megoldjuk a kapott lineáris programozási feladat grafikus módszer.
Építünk az ODR feladat. Feltételek nonnegativeness félig meghatározott sík granichnyim egyenes x1 = 0, és x2 = 0, ill.
Lineáris egyenlet írja le pontok halmaza feküdt egy egyenes vonal. Lineáris egyenlőtlenségek ismertet egy bizonyos területen a gépen. Határozza meg, mely része a sík által leírt egyenlőtlenség
;
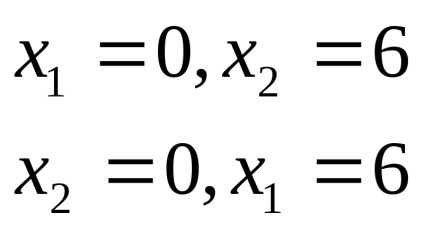
.Ez épül közvetlenül átmegy a (0, 6) és a (6 0). Annak meghatározásához, amely megfelel a gépet, akkor ki kell választania bármely pontján nem tartozik egy egyenes vonal. Mi választjuk ki a kezdőpontot (0, 0), és ebben az esetben az egyenlőtlenség szerezni 0≤12. Ez az állítás igaz, ezért az egyenlőtlenség megfelel az alsó fél-sík.
Hasonlóképpen, mi határozza meg a gépet a többi korlát.
A metszéspontja ezen alsó fél-síkok, amelyek mindegyike által meghatározott megfelelő egyenlőtlenség a rendszer, és kielégíti a nem-negativitás körülmények OAVSD definiál egy sokszög. A bármely pont koordinátáit tartozó tartomány érvényes megoldást a problémára. (1. ábra)
A megtalálása a maximális érték a célfüggvény, amikor ábrázoltuk a probléma megoldásának a lineáris programozás segítségével a gradiens vektor, amelynek koordinátái részleges származékok a célfüggvény.
Ez a vektor irányát jelzi legmeredekebb változás a célfüggvényt. Közvetlen 2x1 + 3x2 = egy (a - állandó) merőleges, a gradiens vektor,

;
Az érték a célfüggvény ezen a ponton:
max f (x) = 2 * 3 * 4 + 2 = 14
Következtetés: A cég profitot maximalizálni, és lesz 14 pénzegység ha a termék az 1. típusú kiadásra kerül az összeg 4 termék, és a termékek a 2. típusú mennyiségben 2 termék.
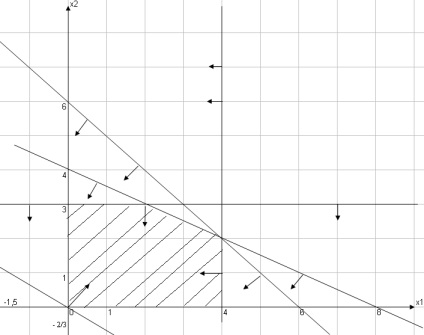
Ábra 1. Grafikus oldatot ZLP.
Mi megfogalmazni és megoldani a kettős problémát. A dualitás, mi a probléma megoldására kézhezvételét eladásából származó bevétel az erőforrások nem kevesebb, mint a kapott összeget a gyártási folyamat során.
Építünk a kettős problémát az eredeti:
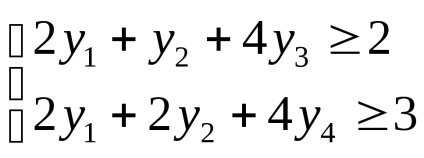
Az első dualitás, van:
F (X *) = Z (Y *), azaz Az optimális értékek a cél funkciók azonosak.
Mivel az optimális terv az eredeti probléma x1 = 4; x2 = 2, és a feltétel nem-negativitás, majd a tétel a komplementer pangást a kettős száma Y1 és Y2 * * egyenlet érvényes:
Z (Y *) = 12 * 8 + 0,5 * 1 + 0 * 16 + 0 * 12 = 14
Kettős értékelés megállapította helyesen.
Gazdasági értelemben feladatokat.
A társaság nyeresége lesz maximális, és lesz 14 pénzegység ha a termék az 1. típusú kiadásra kerül az összeg 4 termék, és a termékek a 2. típusú mennyiségben 2 termék. Összetétele és oldja meg a problémát, hogy egy minimális, azt látjuk, hogy az optimális termelési program és vektor erőforrások termelési veszteségek nulla becsléseket.