jelek egy paralelogramma
Előadás a leckét
Cél: Annak vizsgálata, a jelei a paralelogramma és megszilárdítani tudásukat a folyamat problémák megoldásához.
célkitűzések:- Oktatás: kialakulása készségek alkalmazása a funkciók egy paralelogramma a problémák megoldása érdekében;
- fejleszti: fejleszteni a logikus gondolkodás, a figyelem, a készségek, önálló tanulás, önértékelési készségek;
- iskolai: fokozta az érdeklődést a téma, a képesség, hogy csapatban dolgozni, a kommunikációs kultúra.
Típusa tanulság: tanulás új anyag, az első konszolidáció.
Felszerelés: tábla, projektor, azzal a feladattal, kártyák, bemutatót.
1. szervezése az időt.
Y: Jó napot, fiúk! Ma az osztályban ismét beszélni paralelogramma. Van, hogy végre egy csomó feladatot bizonyítani tételek, és megtanulják, hogy alkalmazza őket a problémák megoldásában. A mottója lecke szavait Le Corbusier: „Körös-körül - geometria.”
2. Frissítse a tanulók tudását.
Néhány diák ad az egyes feladatokat a kártyák tulajdonságait paralelogramma (beállítás választja egymástól függetlenül prezentációt a hivatkozásra, amivel az egérmutatót a forma, de nem több). hallgatni egyenként felelős.

A többi - annak bizonyítására, további tulajdonságainak paralelogramma. (Kérjük, beszélje orálisan bizonyítási majd szinkronizálja interaktív tábla).
1 °. Felezővonal paralelogramma levágja egy egyenlő szárú háromszög.
2 °. Felezővonal szomszédos szögek egy paralelogramma merőlegesek, és bissektrisyprotivopolozhnyh szög párhuzamos vagy kollineáris.
Elkészítése után, hogy hallja a bizonyítékok további tulajdonságainak paralelogramma.
AE felezővonal a szög rossz.
Bizonyítsuk be: ABE - egyenlő szárú.
Mivel ABCD - paralelogramma, akkor BC || AD, míg a sarok szögét EAD = BEA, mint feküdt keresztben párhuzamos vonalak a BC és az AD és a metsző AE. AE - felezővonal a szög BAD, ezért, a szög BAE = sarkában a EAD, tehát a szög BAE = sarok BEA.
A ABE szemzugszög BAE = BEA, így, ABE - egyenlő szárú bázis AE.
Fogalmazza jele egy egyenlő szárú háromszög.
Melyek a szögek BAE egyenlő lehet? Miért?
BE felezővonal szög CBA,
AE - felezővonal a szög rossz.
Amikor közvetlen AE és CK párhuzamos?
e szögek egyenlő, és a BEA <3? Почему?
Ebben az esetben, az AE és a CK-mérkőzés?
Előkészítése a tanulmány az új anyag
Az első munka egy osztály (szájon át).- Mit jelent a „tulajdon” és a „jel”? Adjon példát.
- Mi ennek az ellenkezője?
- Ez mindig igaz állítás visszafordítani ezt? Adjon példát.
3. magyarázatot az új anyag.
W. Minden objektum a saját tulajdonságai és jellemzői. Kérem, mondja meg a különbséget a tulajdonságait jeleket.
Próbáljuk megérteni ezt a kérdést egy egyszerű példát. Dan tárgy - ősz. Mik a tulajdonságait: Jellemzője:

- Mik az állításokat egymáshoz képest tulajdonságait és jellemzőit a tárgyat? (Válasz: fordított)
- Milyen tulajdonságokkal megtanultuk során geometria? Adjon nekik. (Név néhány)
Bármely ingatlan hogy tud-e építeni az ellenkezője az igaz állítás? (Különböző válaszok).
Próbáld ki a következő tulajdonságokkal rendelkezik:
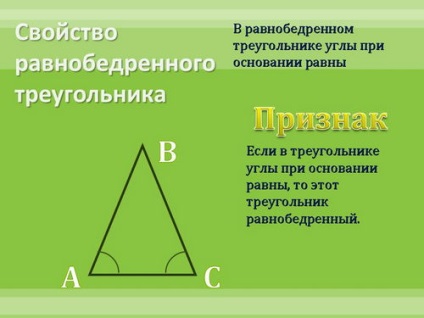
Hogy a következtetést: Bármilyen ingatlan hogy tud-e építeni az ellenkezője az igaz állítás? (Nem, nem az összes)
Most térjünk vissza a négyszög felidézni annak tulajdonságait és megfogalmazni azokat a visszamenőleges jóváhagyásra, azaz (Válasz - jelei paralelogramma). Tehát, a téma a mai leckét: „jelei paralelogramma.”
Tehát, hívja a tulajdonságait paralelogramma.
Adjon inverz tulajdonságai nyilatkozatokat. (Diákok megfogalmazni jelek, azok tanár korrigálja, és újra megfogalmazott)
Bebizonyítjuk ezeket a tulajdonságokat. Az első jel - részletesen, a második - egy rövid, három - saját otthonában.

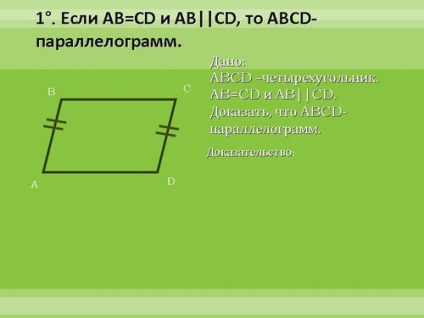
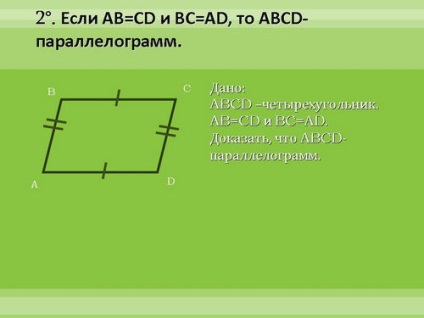
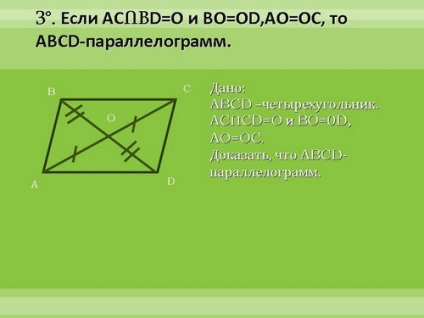
4. Tartozékok anyagot vizsgálták.
Munka a munkafüzet: a probléma megoldására №11 az interaktív táblán a tábla okozhat kevésbé felkészült a hallgató.
Megoldás száma 379 (a döntés, hogy írjon az interaktív táblán). A csúcsok a B és D a ABCD paralelogramma, amelyben AB BC, és éles végzett merőlegesek VC és DM sorra AC. Bizonyítsuk be, hogy a négyszög BMDK - paralelogramma.
Azt, hogy a diákok ideje felkészülni a rajzot.
Adott: ABCD - paralelogramma BK AC, DM
Bizonyítsuk be. hogy: BMDK - paralelogramma.
BKC = DMA-ban a átfogója, és hegyesszöget (a kereszt fekvő szögek párhuzamos vonalak az AD és BC, és a metsző AC, BC = AD, mint az ellenkező oldalon a paralelogramma, BKC és DMA téglalap), majd MD = BK.
BMK és DKM - téglalap alakú, BMK = DKM két Catete (MD = BK, km- közös lábuknál), majd a BM = DK.
A négyszög BMDK ellentétes oldalán egyenlő (MD = BK és a BM = DK), ezért, BMDK - paralelogramma.
5. szét a feladatok (kiválasztott diákok az interaktív tábla, döntést kell ellenőrizni a fedélzeten kattintva a hivatkozásra)
Vissza a kiválasztott feladatok, akkor kap vissza a hivatkozást.
6. Az eredmény a leckét. kihívás.
Tehát, összefoglalva a mai leckét. Kérjük, válaszoljon a kérdéseimre:- Mik az állításokat egymáshoz képest tulajdonságait és jellemzőit a tárgyat?
- Határozza jelei paralelogramma?
- Amire szükségünk jelei paralelogramma?
Házi feladat: c. 43, a második és a harmadik bizonyítási funkció kivitelben, № 380, № 383.
W. Srácok, tanultam ma a jelei a paralelogramma megmutatta nekik, és azt szeretném tudni, hogyan tanult a leckét? (Hagyja az asztalon kívánt csík)