komplex számok
1.Ponyatie komplex szám.
A kifejezés az űrlap z = x + iy nevezzük komplex szám.
A szám x a valós része egy komplex szám Z és jelöljük Re (z), a y - képzetes része egy komplex szám Z és jelöljük Im (z). Száma Z = x + iy és z1 = x - iy nevezett konjugátum. Ha a valós és képzetes része a komplex számok, akkor azt mondják, hogy egyenlő, azaz z1 = z2 vagy x1 + iy1 = x2 + iy2.
Műveletek komplex számok.
1. Az összeg (különbség) a komplex számok.
Z 1 + Z 2 = x 1 + x 2 + i (y 1 + y 2).
2. A termék komplex számok.
Z 1 Z 2 = (x 1 x 2 - y 1 y 2) + i (x 1 + x 2 y 2 y 1).
i² = (0 + i1) (0 + I1) = (0 -1) + i (0 + 0) = -1.
3. Az osztály két komplex szám.

Tekintsük egy derékszögű sík derékszögű koordináta-rendszert Oxy.
Mindegyik i komplex száma Z = x + iy van rendelve egy egyedi pont Z síkban (XY). Oxy sík, ahol minden egyes pont azonosítható a komplex szám, az úgynevezett komplex.
Koordinátatengelyek Ox és Oy, amelyen a valós és a képzetes számok, az úgynevezett valós és a képzetes tengely.
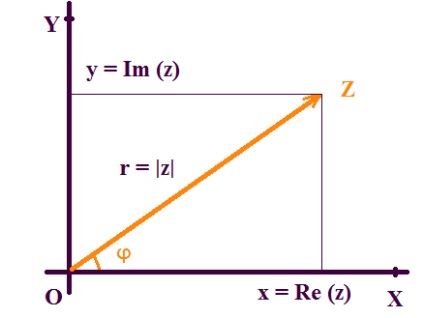
2.Trigonometricheskaya forma egy komplex szám.
Megelőzően bármely pontján a komplex síkban a származási vektor rejthet bizonyos hosszúságú r. Az r szám úgynevezett modulusa a komplex szám Z és jelöljük | Z |.