Változás a változók kettős integrálok

Kiszámítani a kettős integrál \ (\ iint \ limits_R \ right) dxdy> \) néha sokkal kényelmesebb, hogy menjen egy másik koordináta-rendszerben. Ez lehet az oka, hogy az alak a domain integráció, illetve bonyolítja a integrandus. Az új koordinátarendszerben, a számítás lényegesen egyszerűsödik kettős integrál.

Feltételezve, hogy az átalakítsa \ (\ left (\ right) \ to \ left (\ right) \) egy-egy arányát Jacobians direkt és inverz koordináta transzformáció felírható \ [\ left | \ Right) >> \ right) >>> \ right | = \ Left | \ Right) >> \ right) >>> \ right)> ^<- 1>>> \ right | \], feltéve, hogy a nevező nem egyenlő a \ (0 \)

Így a változás változók kettős integrál arra használja a következő három lépésből áll:

Keresse meg a kép \ (S \) az új koordinátarendszerben \ (\ left (\ right) \) kezdeti integrációs tartomány \ (R; \)

Számoljuk ki a Jacobi az átalakulás \ (\ left (\ right) \ to \ left (\ right) \) és rögzítsük a differenciál az új változók \ (dxdy = \ left | \ right) >> \ right) >> \ normalsize> \ right | dudv; \)

Cserélje a integrandusban az eredeti változók \ (x \) és \ (y, \) végző rendre helyettesítési \ (x = x \ left (\ jobbra) \) és \ (y = y \ bal (\ jobbra). \ )

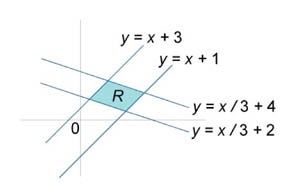
Számítsuk ki a kettős integrál \ (\ iint \ limits_R \ right) dxdy>, \), amelyben a tartomány \ (r \) által határolt vonalak \ (y = x + 1, \) \ (y = x - 3 \) \ ( y = - \ nagy \ frac \ normalsize + 2, \) \ (y = - \ nagy \ frac \ normalsize + 4. \)