Lorentz transzformációk, akkor a fizika
Klasszikus Galileo átalakulás összeegyeztethetetlen a tanításait állomás, és ezért ki kell cserélni. Ezek az új konverziós kell közötti kapcsolat létrehozása a koordinátákat (xy z) és időpontban t megfigyelt a keretben K. és a koordináták (x „Y”. Z »), és a t idő« azonos események megfigyelt a rendszer referencia K ”.
Kinematikai transzformáció képletet a koordináta és az idő SRT úgynevezett Lorentz transzformáció. Ezeket javasolt 1904 eljövetele előtt SRT mint átalakulások, amelyek alapján az invariáns egyenletek elektrodinamika. Abban az esetben, ha a rendszer K „viszonyítva mozog K sebességgel υ mentén az x tengelyen. Lorentz átalakulás formájában:
A Lorentz-transzformáció a következőképpen számos következménnyel jár. Pontosabban, az egyik kell relativisztikus hatás idődilatáció és a Lorentz-összehúzódás hosszát. Tegyük fel például, egy bizonyos ponton x „rendszer K” olyan folyamat időtartama τ0 = t'2 - t'1 (belső idő), ahol a t'1 és t'2 - az órát a rendszerben K „elején és a folyamat végén. A időtartama τ E folyamat a rendszerben K egyenlő lesz
Hasonlóképpen, ki lehet mutatni, hogy a Lorentz-transzformáció követi a relativisztikus hosszkontrakció. Az egyik legfontosabb következménye a Lorentz transzformációk a következtetést a relativitás egyidejűség. Tegyük fel például, két különböző pontban K referencia-rendszer „(x'1 ≠ X'2) egyidejűleg szemszögéből a megfigyelő a K” (t'1 = t'2 = t „), két esemény. Szerint a Lorentz transzformációk, a megfigyelő a K rendszer lesz
Ezért a K rendszerben, ezek az események maradnak térben szétválasztják. Ez nem egyidejű. Sőt, t2 különbség jele - t1 előjele határozza meg a kifejezés υ (X'2 - x'1), azonban néhány képkocka megelőzheti az első esemény a második, míg más vonatkoztatási rendszerek, éppen ellenkezőleg, a második esetben megelőzi az első. Ez a következtetés nem vonatkozik a benzinkutak kapcsolódó eseményeket ok-okozati összefüggéseket. amikor az egyik esemény természetes következménye a másik. Meg lehet mutatni, hogy a STO nem megsértette az okság. és az, hogy a kauzális esemény azonos minden inerciális referencia rendszereket.
A relativitására egyidejűsége térben elválasztott események szemlélteti a következő példa.
Tegyük fel, hogy a keretben K „mentén az x-tengely” még mindig hosszú merev rudat. A központ rudat villanólámpa B. és szerelt végeinél két szinkronizált órák (ábra. 4.4.1 (a)), a rendszer K „tengely mentén mozog x K rendszer sebességgel υ. Egy bizonyos ponton, a lámpa bocsát ki rövid fényimpulzusokat végei felé a rúd. Azáltal egyenlő mindkét irányban a fény a rendszerben K „eléri a végén a rúd egy időben, és az óra, szerelt végét a sáv mutatja ugyanakkor t”. Relatív, hogy a K rendszerben csuklófejek mozgatni sebességgel υ, hogy az egyik vége felé mozog fényimpulzus, a másik végén a világ, hogy utolérjék. Mivel a terjedési sebesség a fény impulzusok mindkét irányban azonos és egyenlő c. Ezután, a szempontból egy megfigyelő a rendszerben K. fényt, mielőtt elérkezik a bal végén a rúd, mint a jobb oldali (ábra. 4.4.1 (b)).
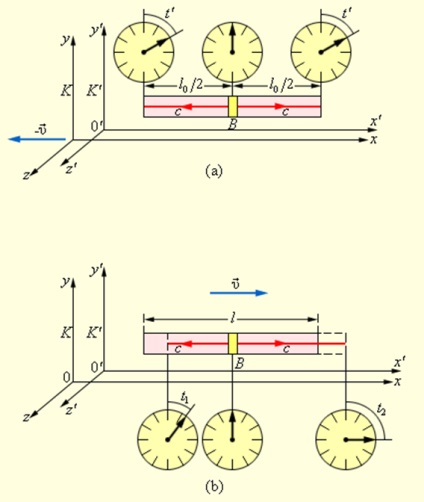
Relativitás egyidejűség. A fény impulzus eléri a végén a szilárd, rúd, míg a keret K „(a), és egyidejűleg nem a rendszer referencia K (b)
Lorentz transzformációk kifejezze a relatív jellegét időszakok és távolságok. Ugyanakkor fontos szerepet SRT együtt egy nyilatkozatot természetére vonatkozó térben és időben játszik a létesítmény állandó fizikai mennyiségekkel alatt nem változik az átmenet az egyik keret a másikra. Az egyik ilyen változó a fény sebessége c. amely SRT abszolút. Egy másik fontos invariáns mennyiség tükröző abszolút jellege tér- és időbeli kapcsolatok közötti intervallum eseményeket.
Tér- és időbeli intervallumban határozzák meg SRT következő összefüggés:
ahol t12 - közötti időszak eseményei hivatkozási rendszert, és l12 - a távolság a pontok, ahol az események történnek azonos keretben. Abban az esetben, amikor egy esemény bekövetkezik a koordináta (x1 = y1 = Z1 = 0) referenciakeret időpontban t1 = 0, és a második - a koordinátái x. y. Z t időpontban. tér- és időbeli között eltelt ezen események írott formában
A Lorentz-transzformáció bizonyítani tudja, hogy a tér-idő intervallum két esemény között nem változott az átmenet az egyik tehetetlenségi rendszerből a másikba. Invariancia intervallum azt jelenti, hogy annak ellenére, hogy a relatív távolságokat és ideig, az áramlás a fizikai folyamatok objektív jellegű, és nem függ a vonatkoztatási rendszer.
Ha az egyik esemény egy flash fény elején a referencia-képkocka a t = 0, és a második - az érkezés az első lámpa egy pont koordinátái x. y. Z t időpontban (ábra. 4.1.3), majd a
és ezért az intervallum a két esemény s = 0. Egy másik referencia koordinátarendszer és a második esemény más lesz, de ebben a rendszerben, a tér-idő intervallum s'értéke nulla lenne, mivel
Bármely két esemény egymással fényjelzés intervallum nulla.
A Lorentz transzformációk a koordinátákat és az időt, akkor kap a relativisztikus sebességgel kívül jogot. Tegyük fel például, a referencia-rendszer K „mentén x” tengely részecske mozog sebessége komponenseket a részecske sebességének és u'x u'z nulla. A sebesség a részecskék a rendszer lesz egyenlő K
megtalálható differenciálódása a Lorentz-transzformáció képletek:
Ezek a kapcsolatok kifejezésére relativisztikus sebességgel kívül törvény arra az esetre, ha a részecske mozog párhuzamosan a relatív sebességét K keretek és K”.
Ha υ < Ha a rendszer K „mentén x” tengely körül, olyan sebességgel u'x = c alkalmaz impulzus fény, akkor az impulzus sebessége ux a rendszerben megszerezni K Így a referencia-rendszer K fényimpulzus kiterjed az X tengely mentén a c sebességgel. amely összhangban van a posztulátum invarianciájának a fénysebesség.Kapcsolódó cikkek