Eltávolítása a gyökerek a mértéke nagyobb, mint 2

A komplex számok lehetővé teszi, hogy fontolja meg néhány nehéz esetekben, amikor eltávolítja a gyökerek mértékben nagyobb, mint 2.

Azt már tudjuk, hogy a $ \ sqrt $ +1 vagy -1, $ \ sqrt $ egyenlő + i és -i.

És mi van a negyedik gyöke 1 ($ \ sqrt [4] $)? Nyilvánvaló (1) x (1) x (1) x (1) = + 1, azaz 1 - az egyik a negyedik egyik gyökérben. Hasonlóképpen, (-1) x (-1) x (-1) x (-1) = + 1, azaz -1 - ez is az egyik a negyedik egyik gyökérben. De nem átnézte az összes lehetőséget. Mi a helyzet a kifejezést $ (+ i) \ alkalommal (+ i) \ alkalommal (+ i) \ alkalommal (+ i) $? Az eredmény szorzata $ (+ i) \ alkalommal (+ i) $ - ez a -1. Ezért, $ (+ i) \ alkalommal (+ i) \ alkalommal (+ i) \ alkalommal (+ i) = (- 1) \ alkalommal (-1) = + 1 $. Ez azt jelenti, hogy a + i - ez a harmadik negyedik egyik gyökérben. Hasonlóképpen, meg tudjuk mutatni, hogy -і - ez a negyedik gyöke a negyedik foka 1.

Ezért célunk a következő választ: ($ \ sqrt [4] $) = + 1, -1, + i, -і. Hasonlóképpen, tudjuk mutatni, hogy ($ \ sqrt [4] $) egyenlő $ + \ sqrt $, $ - \ sqrt $, $ + \ sqrt $ vagy $ - \ sqrt $, azaz, ez a probléma négy egyenértékű megoldások .

És mi van a $ \ sqrt $? A válasz egyszerű. ($ \ Sqrt $) - ez egy olyan szám, amely ha kell szorozni magát a legjobban, ad i. Ezért ($ + \ sqrt $) x ($ + \ sqrt $) = + i Ezért, $ (+ \ sqrt) \ alkalommal (- \ sqrt) \ alkalommal (+ \ sqrt) \ alkalommal (- \ sqrt) = ( + i) \ alkalommal (+ i) = -1 $.

Következésképpen, ($ + \ sqrt $) az egyik a gyökerek a negyedik fokozat (-1), a másik gyökerek $ - \ sqrt $, $ + \ sqrt $ és $ - \ sqrt $.

Ugyanígy lehet mutatni, hogy bármennyi négy gyökerei a negyedik fokozatot.

Megmutattuk, hogy minden szám két négyzetgyök, és négy gyökerei a negyedik fokozatot. Azt is feltételezik, hogy minden szám három gyökerei a harmadik fokozat, az öt gyökerei az ötödik fokozat, a hat gyökerei a hatodik fokozat, negyvenöt gyökerei a negyvenötödik fokozat, és így tovább. Ez az állítás teljesen igaz, de ahhoz, hogy bebizonyítsam, igényel bonyolult matematikai apparátust, amely nincs, amíg vesszük azt a hitet.

Azonban tudjuk ellenőrizni ezt az állítást a gyökér a harmadik foka. Mi például egyenlő a köbgyökét 1, vagy ($ \ sqrt [3] $)? Először is, (+1) x (+1) x (1) = + 1, vagyis az egyik egy kocka gyökerei 1.

És mi van a másik kettő? Most pedig a negatív számokat. (-1) x (-1) x (-1) = (+ 1) x (-1) = - 1.

Így -1 nem gyökér a kocka 1. Sőt, lehet mutatni, hogy nincs valós szám, és egyik képzeletbeli (akár 1 vagy -1) emelte a harmadik erő, ez nem eredményezi + 1 .

Tehát a gyökere minden, és a másik két egyszerűen nincs?

Ez a két gyökerek létezik, de az a komplex számok. Most mutatják be értékeket, akkor nézd meg, mit ezek a számok a köbön. A másik két kocka gyökerei 1 + - jelentése ($ - \ frac12 + \ frac12 \ sqrt $) és ($ - \ frac12- \ frac12 \ sqrt $). Nézzük ezt az állítást.

If ($ - \ frac12 + \ frac12 \ sqrt $) - az egyik kocka gyökerei egy, az azt jelenti, hogy ($ - \ frac12 + \ frac12 \ sqrt $) 3 vagy $ (- \ frac12 + \ frac12 \ sqrt) \ alkalommal (- \ frac12 + \ frac12 \ sqrt) \ alkalommal (- \ frac12 + \ frac12 \ sqrt) $ egyenlő 1.

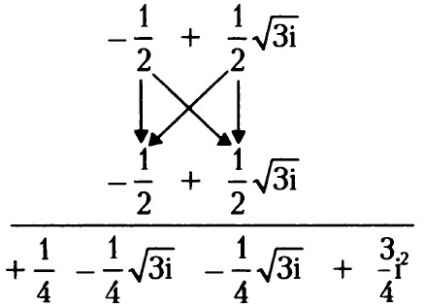
Két képzeletbeli köztes eredmény lehet hajtani, a számok összege ($ - \ frac14 \ sqrt $) és ($ - \ frac14 \ sqrt $) egyenlő ($ - \ frac12 \ sqrt $). Ami a $ \ frac34i 2 $ ez egy valós szám egyenlő $ - \ frac34 $. Most adjuk hozzá a két valós elemei a kifejezést: $ \ frac14- \ frac34 = - \ frac12 $, hogy a szorzata $ - \ frac12- \ frac12 \ sqrt $.

Ez az eredmény kell újra megszorozva ($ - \ frac12 + \ frac12 \ sqrt $).

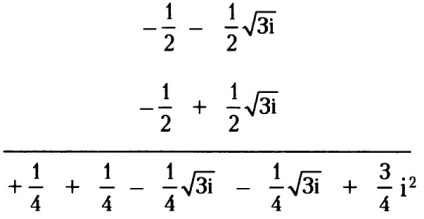
Két képzetes komponensei az expresszió-zheniya ($ - \ frac14 \ sqrt $) és ($ - \ frac14 \ sqrt $) összege 0, úgy, hogy el lehet hanyagolni. A több $ \ frac34i $ 2 egy valós szám, mint én 2 = -1, azaz $ \ frac34i $ 2 = $ \ frac34 $. Add meg a $ \ frac34 $ fennmaradó köztes eredmény $ \ frac14 $, és kap 1 Így ($ - \ frac12 + \ frac12 \ sqrt $) 3 1.

Ugyanígy meg lehet építeni a számos harmadik fokozat ($ - \ frac12- \ frac12 \ sqrt $) 3:

Hasonlóképpen, ki lehet mutatni, hogy a Num-la -1 három gyökerei a harmadik fokozat, melyek közül kettő komplex. három köbméter gyökerek és számok i és -i.

Kapcsolódó tartalom:

Oszd meg barátaiddal: