Meghatározása és grafikonok trigonometrikus függvények
A szögek (függvényargumentumok): \ (\ alpha \), \ (x \)
Trigonometrikus függvények: \ (\ sin \ alpha \), \ (\ cos \ alpha \), \ (\ tan \ alpha \), \ (\ gyermekágy \ alpha \), \ (\ sec \ alpha \), \ ( \ CSC \ alpha \)
A valós számok halmazán: \ (\ mathbb \)
A koordináták a kör: \ (x \) \ (y \)
kör sugara: \ (r \)
Egész számok: \ (k \)
A trigonometrikus függvények elemi függvények, ami a szög érv. Használata trigonometrikus függvények leírt kapcsolatok oldalai között és az éles sarkok a téglalap alakú háromszög. Alkalmazások trigonometrikus függvények rendkívül sokfélék. Például bármilyen periodikus folyamat leírható összegeként trigonometrikus függvények (Fourier-sor). Ezek a funkciók gyakran jelennek meg a megoldás, differenciálegyenletek és funkcionális.
Trigonometrikus függvények tartalmazza a következő 6 funkció: Sine. koszinusz. érintőleges. kotangensét. metsző és koszekáns. Minden ilyen funkció van egy inverz trigonometrikus funkció.
Geometriai meghatározása trigonometrikus függvények kényelmesen belépett a készülék használata kört. Az alábbi ábra egy kör sugara \ (r = 1 \). Jelöli a pontot a kör \ (M \ left (\ right) \). A bezárt szög a sugár vektor \ (OM \) és a pozitív tengely irányában \ (Ox \) egyenlő \ (\ alpha \).
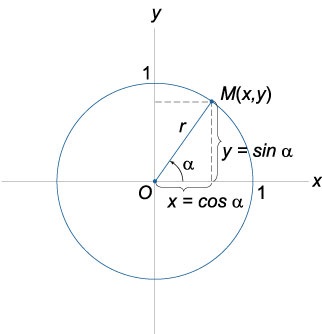
Sine szög \ (\ alpha \) az aránya az ordináta \ (y \) pont \ (M \ left (\ jobbra) \), a sugárral \ (r \):
\ (\ Sin \ alpha = y / r \).
Mivel a \ (r = 1 \), a szinusz egyenlő az ordináta a pont \ (M \ left (\ right) \).
Koszinusza szög \ (\ alpha \) az aránya a abszcisszák \ (x \) pont \ (M \ left (\ jobbra) \), a sugárral \ (r \):
\ (\ Cos \ alpha = x / r \)
Szög tangense \ (\ alpha \) az aránya az ordináta \ (y \) pont \ (M \ left (\ jobbra) \) az EE abszcisszán \ (x \):
\ (\ Tan \ alpha = y / x, \; \ x \ ne 0 \)
Kotangensét szög \ (\ alpha \) az aránya a abszcisszák \ (x \) pont \ (M \ left (\ jobbra) \) egy ordinátán \ (y \):
\ (\ Cot \ alpha = x / y, \; \; y \ ne 0 \)
Szekáns szög \ (\ alpha \) - a hányadosa sugara \ (r \), hogy az abszcissza \ (x \) pont \ (M \ left (\ right) \):
\ (\ Sec \ alpha = r / x = 1 / x, \; \ x \ ne 0 \)
Koszekáns szög \ (\ alpha \) - a hányadosa sugara \ (r \) az ordinátán \ (y \) pont \ (M \ left (\ right) \):
\ (\ Csc \ alpha = r / y = 1 / y, \; \; y \ ne 0 \)
Az egység kör vetítési \ (x \), \ (y \) pont \ (M \ left (\ jobbra) \), és a sugara \ (r \) alkotnak derékszögű háromszög, azzal jellemezve, \ (x, y \) a lábak, és \ (r \) - átfogója. Ezért, a fenti definíció trigonometrikus függvények az alkalmazás egy téglalap alakú háromszöget a következőképp alakul:
Sine szög \ (\ alpha \) az aránya a másik lábát a átfogója.
Koszinusza szög \ (\ alpha \) az aránya a átfogója a szomszédos láb.
Szög tangense \ (\ alpha \) nevezzük az ellenkező oldalon egy szomszédos.
Kotangensét szög \ (\ alpha \) nevezzük a szomszédos oldalán egy ellentétes.
Szekáns szög \ (\ alpha \) képviseli az arány a átfogója a szomszédos láb.
Koszekáns szög \ (\ alpha \) képviseli az arány a átfogója a másik lábát.
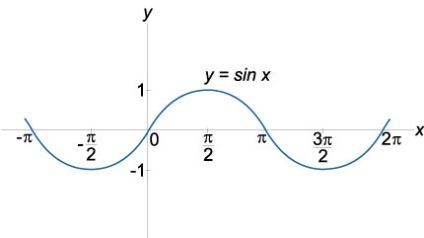
A grafikon a szinusz
\ (Y = \ sin x \), a domain a meghatározás: \ (x \ in \ mathbb \), az értéktartomány: \ (- 1 \ le \ sin x \ le 1 \)
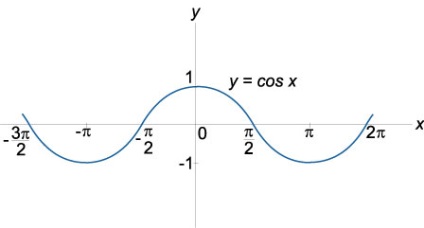
Ábrázolja a koszinusz függvény
\ (Y = \ cos x \), a domain a meghatározás: \ (x \ in \ mathbb \), az értéktartomány: \ (- 1 \ le \ cos x \ le 1 \)
Ábrázolja a tangens függvény
\ (Y = \ tan x \), a domain a meghatározás: \ (x \ in \ mathbb, x \ ne \ left (\ right) \ pi / 2 \), az értéktartomány: \ (- \ infty