Használata szimmetria egy egyenes vonal foglalkozó építési problémák - studopediya
Definíció. Hagyja, hogy a sík által meghatározott vonal és és két A és B pontok Ezeket nevezik szimmetrikus, ha:
2) közvetlen és felezi egy szegmens (9.).
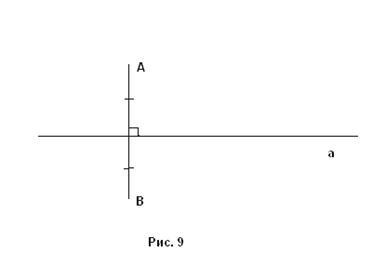
Közvetlen és így hívják a szimmetriatengely.
Definíció. A következő egy síkban úgynevezett szimmetria tengelyére vonatkoztatva vagy tengelyirányú szimmetria, mintha minden egyes pont egy síkban van rendelve egy pont szimmetrikus hozzá képest egy tengely A1.
Tulajdonságok tengelyszimmetriát:
1). Amikor tengelyszimmetrikus egyenes vonalban halad;
2). Ha az axiális szimmetria a szegmens válik egyenlő vele szegmens;
3). Amikor tengelyszimmetrikus szög válik szögben egyenlő vele;
4). Tengelyszimmetriát egy mozgalom.
Tekintsük a példát az alkalmazás szimmetria.
6. példa .A közvetlen k, és a két A és B pont, nem fekszenek ezen a vonalon. K talál egy pontot az X összeget AX + XB minimális volt.
Elemzés. Tegyük fel, hogy a probléma megoldódott. Ha A és B egymással átellenes oldalain K, akkor nyilvánvaló, hogy X - a metszéspont az AB és a közvetlen k. Ha A és B pontok egyik oldalán k, az megjelenik egy viszonylag szimmetrikusan k, így a pont B1, úgy, hogy a belső viszkozitás, és így XB1 = X pontot kell feküdjön intervallumban AV1 (ábra. 10).
Building. Ha a A és B pontok két ellentétes oldalán k, majd tartsa a szegmens AB és keresztezi k a kívánt ponton X.
Ha A és B az egyik oldalon a k, akkor jelenik meg szimmetrikus k, megkapjuk a pontot B1. Miután kiadások a szegmens AB, megkapjuk a kívánt ponton X.
Bizonyítás. Az első esetben a bizonyíték nyilvánvaló. A második esetben, ha A és B egyik oldalán K: legyen Y - bármely más pont a vonal a K, eltér H. Ezután, a szimmetria tulajdonságok azt látjuk, hogy BY = B1 Y, és a háromszög-egyenlőtlenség van AY + YB = = AY + YB1> AB = AX + XB1 (10 ábra).
Tanulmány. Probléma van megoldás, és hogy mindig egyet.
Példa 7.Postroit AVSD négyszög, ha definiált szegmenseket, amelyek oldalai AB = a, VS = b, DM = c = d YES és ismert, hogy az AC átló felosztja a felére az A szög (ábra. 11).
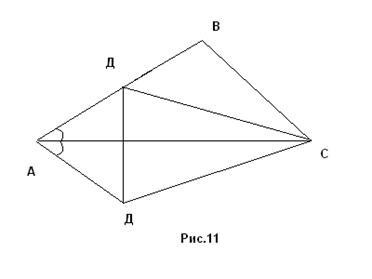
Elemzés. Tegyük fel, hogy a probléma megoldódott, és a négyszög AVSD - kérik. Ezután a két fél AB és AD még egy. Mert határozottságot, legyen a> d. Bemutatás szimmetrikus pont képest a D vonal AC kap az AB oldalon pont D1. In háromszög VSD1 ismert minden oldalról: VS = b, DM = C, D1 B = a - d. Tehát D1 BC háromszög van felépítve, majd épített az egész téglalap.
Building. Épület egy háromszög D1 BC három oldalról BC = b, CD = c, D1 B = a - d. Ezután felé VD1 továbbra azon a ponton túl a D1 és a elhalasztja a szegmens AB = a, megkapjuk az A. pontja Készítünk egy D pontot, D1 pont szimmetrikus az AU. Csatlakoztassa a pontok az A és D, A és C négyszög AVSD - szükséges.
Bizonyítás. Nyilvánvaló az építkezést.
Elemzés. Konstrukció lehetséges, ha van lehetőség, hogy egy háromszög D1 BC, azaz A háromszög-egyenlőtlenség b <с + а + d, с <в + а – d, а – d <в + с. В этом случае задача имеет одно решение.