Splines, véges függvények
„Splines. Véges funkciókat. Alapfogalmak találkozót. Schönberg bordák "
Funkciók hasonló ahhoz, amit most az úgynevezett bordák ismertek voltak matematikusok sokáig, kezdve minimum Euler, de az intenzív vizsgálat indult, sőt, csak a közepén a XX században. 1946-ban Isaac Schoenberg alkotta meg a kifejezést, mint a megjelölés az osztály polinomiális spline. 1960-ig, bordák többnyire elméleti kutatási eszköz, gyakran jelennek meg különféle megoldásai szélsőséges és variációs probléma, különösen közelítés elmélet.
1960 után a számítástechnika fejlődése kezdte használni spline a számítógépes grafika és modellezés, hogy továbbra is ezen a napon.
Under spline (az angol spline -. Szíj, gereblye) általában szakaszosan egybeesik funkciók egyszerűbb természet minden elemét saját domain választásnál.
Classic egy változó spline a következőképpen készítjük: a domain van osztva egy véges számú szegmensek, amelyek mindegyike spline egybeesik néhány algebrai polinom. A legnagyobb fokú polinommal az úgynevezett mértéke a spline. A különbség mértéke között a spline és a sima a kapott hiba nevezett spline. Például, van egy folyamatos sokszögű spline fokú 1 és hiba 1.
Splines számos felhasználási területe van a matematikai elmélet, és a különböző számítástechnikai alkalmazások. Különösen a bordák két változó erősen meghatározására használt felületek a különböző rendszerek számítógépes szimuláció.
1.1 Bezier görbéket
Bezier görbe vagy Bezier-Bernstein fejlesztették ki a 60-as években a XX század függetlenül Pierre Bézier és Paul de Casteljau.
Görbéket először a nyilvánosság elé 1962-ben a francia mérnök Pierre Bezier, akik fejleszteni őket függetlenül de Casteljau, használják őket, hogy a számítógéppel segített tervezés gépjármű szervek. Görbéket name nevű Bezier nevezetesen de Casteljau úgynevezett rekurzív módon azokat meghatározó fejlett görbék (de Casteljau algoritmus).
Ezt követően ez a felfedezés lett az egyik legfontosabb eszköz a számítógéppel segített tervezés és a számítógépes grafikai programok.
Bezier görbe - paraméteres görbe által adott kifejezést:
- referencia-funkció vektorok komponenst csúcsok, és
, közelítése az első deriváltját
.
A fennálló ilyen központi tétel, valamint egy másik sorozatában a bevált Strang-Fix elmélet, különösen a létezését funkciók kielégítő (2,7), ad egy algoritmust az építési alapvető funkcióit kompakt támogatást a szükséges közelítés tulajdonságait.
3. B-spline Schoenberg
A numerikus matematika úgynevezett B-spline spline függvény, amelynek a legalacsonyabb hordozót egy adott mértékben, simaság és bomlási sorrendben domént. Az alaptétel kimondja, hogy minden spline függvény egy adott fokozat, simasága és domain leírható lineáris kombinációja B-spline és azonos mértékű simasága ugyanabban a tartományban. [1] A kifejezés B-spline vezették J. Schoenberg és egy összehúzódása a kifejezés „alap spline”. [2] B-spline lehet kiszámítani az algoritmus de Boor, amelyek rezisztensek.
A CAD rendszerek és a számítógépes grafika B-spline kifejezés gyakran leírja a spline görbe, ami által meghatározott spline függvények, által kifejezett lineáris kombinációi a B-spline.
Ha az egységek egymástól egyenlő távolságra, azt mondják, hogy a B-spline egységes, különben ez az úgynevezett inhomogén.
Amikor a csomópontok száma egybeesik a mértéke a spline, B-spline egy Bezier görbét elkorcsosul. Ez képezi az alapvető funkciója határozza meg a helyét a csomópontok. A méretezés vagy párhuzamos szállítása alapján vektor nem befolyásolja az alapvető funkciót.
Spline szereplő konvex burka az ellenőrző pontokon.
Alapvető spline fokú N:
.
Ez nem tűnnek csak intervallumon [ti, ti + n + 1], azaz .:
Más szóval, a változás egyik ellenőrző ponton csak érinti a helyi viselkedését a görbe, hanem a globális, mint abban az esetben, Bezier görbék.
A bázisfüggvényt lehet beszerezni Bernstein polinom
B-spline és néhány, a leggyakrabban használt bázisok
Tétel Strang-Fix azt jelzi, hogy ha a szabványos véges funkció
alapján választják meg feltétel (2,7), majd a (2.4) alapján szerkesztett annak fordítások, majd rendelkeznek jó közelítéssel tulajdonságokkal.
Schoenberg felajánlott egy érdekes osztály műveleteit kielégíti (2.7). függvény
az úgynevezett B-spline (Schoenberg) fokozatot
, ha a Fourier-transzformáció adja
Mint látható, a függvény (6.8) követelményeknek megfelel (6.7).
Alapján lépések
Elég könnyű azt mutatják, hogy a
Ez jelenti egy közelítése egy folytonos egyenes vonal, amely nem folytonos származékok. sebességgel közelítés
Azt másodrendű sebességgel
- először. Ez a közelítés a leggyakrabban használt megoldására differenciálegyenletek másodrendű előrejelzési módszer. Ez vezet a legegyszerűbb képletek a integrálok és a legtöbb ritka mátrixot a számítás.
Ezen túlmenően, ezen az alapon, tekintettel arra, hogy p = 1, van egy funkció - a közelítő függvény
egybeesik a függvény értékei a rácspontok
, amely lehetővé teszi, hogy gyorsan megtalálja a kezdeti közelítés
.
Ez egy szakaszonként harmadfokú spline polinom, amelyet úgy kapunk, konvolúció:
.
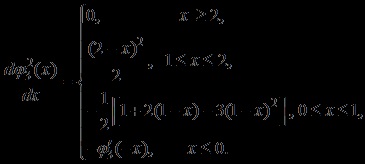
Media Size
emelkedett négy (
). Megjegyzendő, hogy a folytonosság biztosítása a pontok a második derivált
. Mint már említettük, a közelítés a norma
negyedrendű, amelynek mértéke
5. J. Alberg Nilson J. Walsh - .. Az elmélet bordák és alkalmazásaik