K-közép klaszterezés és az aszimmetrikus távolságmérés - sok szám
K-medián clustering és aszimmetrikus távolságmérés
Jellemző, hogy a szokásos csoportosítás K-euklideszi távolság elég, de itt állunk szemben néhány probléma, hogy gyakran előforduló adatok csoportosítási, nagy spread (függetlenül attól, hogy a lakossági, akár besorolása szövegek, illetve bioinformatikai).
A K-közép klaszterezés
Az első nyilvánvaló probléma az, hogy a klaszter központok vannak kifejezve tized egység, annak ellenére, hogy a vektor tranzakciók minden ügyfél - pontosan nulla vagy egy. Mit is jelent valójában a 0,113 az üzlet? Azt akarom, hogy klaszter központokat kifejezhető ügylet vagy annak hiánya!
Ha megváltoztatja egy kicsit csoportosítási algoritmus, hogy csak vektor tartja az ügyfelek tranzakciókat, ez már ismert csoportosítás szerint k-mediánértékeknek helyett k-eszközökkel.
És ha nem akarja megváltoztatni az euklideszi távolságot, minden amire szüksége van -, hogy adjunk egy bináris állapot (bin) a „keresd a megoldást” minden klaszter központ.
De ha a klaszter központok már bináris, hogyan kell használni az euklideszi távolságot?
Azt viszont, hogy a megfelelő távolság mérése
Ha áttér K-k-medián, az emberek általában ne használja az euklideszi távolságot és kezdi el használni valamit az úgynevezett Manhattan távolság, vagy metrikus város blokk.
Annak ellenére, hogy a távolság a pont a B pont mérése egy egyenes vonal, a taxi a Manhattan kell navigálni hálózatán keresztül egyenes utcák, ahol a forgalom csak északi, déli, keleti vagy nyugati. Ezért, ha látható. 2-13 látja, hogy a távolság a táncos-tanuló és klaszter központja körülbelül 4,47, ez Manhattan távolság egyenlő 6 méter (4 m + 2 méter mélyen keresztben).
Ami a bináris adatok, mint például értékesítési adatok, Manhattan közötti távolság a klaszter központ és vásárol egy vektor - ez csak néhány következetlenséget. Ha a központ a klaszter 0 I 0 a távolság ebben az irányban 0, és ha van 0 vagy 1, vagyis a számok nem egyeznek, akkor az irányt a távolság azonos 1. hozzáadása őket, akkor kap a teljes távolságot, ami egyszerűen száma eltérések.
Van Manhattan távolság kulcsszerepet játszik a döntésben?
Mit jelent a „az ügyfél tett foglalkozik?” Ez azt jelenti, hogy nagyon szeretett volna vásárolni ezt a terméket!
Mit jelent a „a vevő nem tett foglalkozik?” Ez azt jelenti, hogy nem akarjuk, hogy ez a termék annyira, mint az, amelyik megvette? Ugyanígy vannak erős pozitív és negatív jelek? Talán szeret pezsgőt, de már van raktáron a pincében. Talán csak nem látni a hírlevél ebben a hónapban. Sok oka van annak, hogy valaki valamit csinál, de csak néhány - miért intézkedéseket hozzanak.
Más szóval, meg kell figyelni, hogy megrendelések, hanem azok hiánya.
Vannak bonyolult mot - „aszimmetria” az adatokat. Az egységek sokkal értékesebb, mint nulla. Ha az egyik ügyfél ugyanaz másik három egység, akkor ez sokkal fontosabb mérkőzés, mint a harmadik vásárló a három nullát. Mi elkapja a szemét -, így ez egy kis egységek számát az adatok -, hogy ők „szórványos adatok”!
Szükség van egy aszimmetrikus távolság számítás. És a változó adatokat egy bináris kódot, mint ezek a megrendelések bor van egy csomó jó lehetőségeket.
Valószínűleg a legelterjedtebb módszer a számlálás aszimmetrikus távolsági adatokat formában hívják 0-1 koszinusz távolság.
Távolság a koszinusz - nem is olyan rossz, annak ellenére, trigonometria
A legegyszerűbb módja annak, hogy elmagyarázza, mi az a koszinusz távolság - az, hogy elemezze a „közelség koszinusz”.
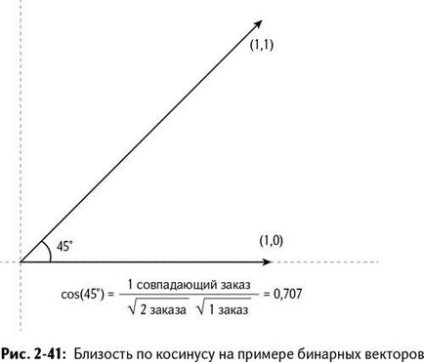
Vegyünk egy pár kétdimenziós bináris vektorok (1,1) és (1,0). Az első vektor, mind az áruk megrendelt, míg a második, csak az első. El tudja képzelni ezeket a vektorokat, és úgy látjuk, hogy a szög - 45 ° (Ábra 2-41.). Reach szögmérő - ellenőrizze.
Azt mondhatjuk, hogy a közelség egyenlő a koszinusza 45 fok, ami 0,707. De miért?
Kiderült, hogy a koszinusz a szög a két bináris megrendelések - jelentése:
A találatok számát megrendelések két vektor osztva a termék a tér gyökerei a megrendelések száma az első és a második vektor
Esetünkben a két vektor (1,1) és (1,0) van egy megfelelő sorrendben, hogy a számláló és a nevező értéke 1 - négyzetgyök kettő (2 megkötött ügylet) szorozva négyzetgyök egyik üzlet. Az eredmény 0.707 (ábra. 2-41).
Ami figyelemre méltó ebben a számításban?
• számláló formula pedig csak meccsek trade, azaz ez aszimmetrikus, és ezért nagyon alkalmas arra, hogy ebben az esetben;
• négyzetgyöke a tranzakciók száma minden vektor a nevezőben felhívni a figyelmet arra a tényre, hogy a vektor, amely elkötelezett az összes tranzakciót - nevezzük olvashatatlanná - sokkal távolabb a többi vektor, mint az elkövető ugyanazon ügylet, és nem követtek még sokan mások. Meg kell egyeznie vektorok „ízek”, amelyek azonosak, és nem egy vektor, amely egy „íz” a másik.
• bináris adatokat, ez a közelség 0 és 1 között, és a két vektor nem működik 1, amíg az összes megrendelését nem egyeznek. Ez azt jelenti, hogy 1 - a közelsége a koszinusz távolság lehet használni, mint egy intézkedés úgynevezett koszinusz távolság, amely szintén változik 0-1.
És most minden ugyanaz, de az Excel
Itt az ideje, hogy egy esélyt, hogy bizonyítsanak K-közép klaszterezés a koszinusz távolságok.
Klaszterek segítségével koszinusz távolság is nevezik a gömb alakú k-közegben. 10. fejezet, látni fogja a gömb alakú k-means R.
Mi következetes és folytassa k = 5.
Ismét indul a másolatot 5MS és nevezze meg újra, ezúttal 5MedC. Mivel a klaszter központokat kellene bináris, akkor el kell távolítani az összes, hogy már írt „keresni a megoldást.”
Az egyetlen dolog igénylő változás van (kivéve hogy a bináris kifejezéseket a „Keresés megoldást” a k-mediánok), - a számítás a távolság a sorok 34 38. Kezdj M34 sejtek közti távolság Adams és a központ a klaszter 1.
Számolni véletlenek itt Adams és 1. klaszter, alkalmazni kell a két oszlop SUMPRODUCT / SUMPRODUCT. Ha egyikük vagy mindkettő megtalálható 0, akkor a karakterlánc üres, de ha mindkettő 1, akkor ez egy véletlen egybeesés feldolgozott SUMPRODUCT / SUMPRODUCT 1 szorozva 1 marad 1.
Ami a vonás a tranzakciók száma történt a vektor, egyszerűen SQRT // root kivetett SUM // ÖSSZEG vektor. Így a távolság egyenlet a következőképpen írható fel
Ügyeljen arra, hogy az „1” az elején egy képlet, amely megkülönbözteti a közelség a koszinusz távolság a koszinusz. Továbbá, ellentétben az euklideszi távolságot, koszinusz távolság számítás nem igényel a használata tömbképletek.
Különben is, amikor behelyezi a M34, meg kell hozzá hibaellenőrzési esetén a klaszter központ lesz 0:
Hozzáadása formula IFERROR / IFERROR megszünteti osztás 0. És ha valamilyen okból, „Megoldások” választja ki a klaszter központ, teljesen álló 0, akkor feltételezhető, hogy ez a központ található, a parttól 1 a többi (1 a legmagasabb bináris változó értéke).
Akkor másolja le a M34 a M38 oszlop és módosíthatja a hivatkozásokat H oszlop I, J, K és L Akárcsak az euklideszi távolság, akkor használja az abszolút hivatkozások ($) a képlet, így húzza valahol tetszik sérelme nélkül, az oszlop a klaszter központ.
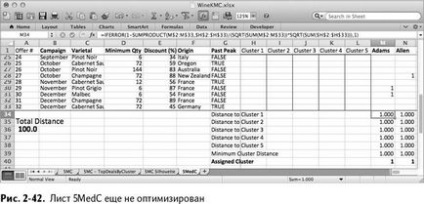
Így megkaptuk 5MedC lista (ábra. 2-42), amelynek abszolút azonos lap 5MS, akikkel korábban működött.
Most, hogy megtalálják a klaszterek, nyissa meg a „Keresés megoldás”, és változtassa meg a feltétele "<= 1» для Н2:L33 на бинарное.
Kattintson a "Run". Pihenhet egy fél órát, amíg a számítógép keresi a legjobb klaszterek az Ön számára. Észre fogod venni, hogy az összes klaszter központ most - bináris, hogy a feltételes formázás két árnyalat, ami nagyban javítja a kontrasztot.
Értékelés kereskedik az 5-medián klaszterek
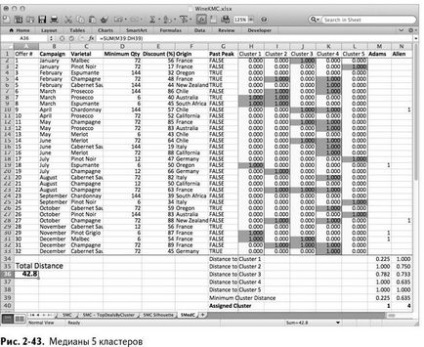
Befejezését követően „A keresés megoldás” már kialakult 5 klaszter központok, és minden - egy csomó is rámutatva, hogy a tranzakció előnyös, klaszter. Az én „Search Solutions” biztosítja az optimális objektív értékét 42,8, bár a tiéd lehet egészen más (ábra. 2-43).
Nézzük meg ezeket a klasztereket, a számítási módszer a tranzakciók, amit használt k-eszközökkel. Ehhez először másolja a 5MC lap - TopDealsByCluster fülre, és nevezd meg 5MedC - TopDealsByCluster.
A klaszter lehet némileg eltér az enyémtől, és annak érdekében, valamint a készítmény az evolúciós algoritmus, de remélhetőleg a különbség nem szignifikáns. Menjünk át a klaszterek, és hogyan ezt az algoritmust közös ügyfelek.
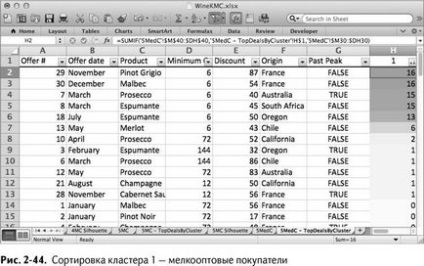
Rendezése 1. klaszter: úgy tűnik, hogy kis nagykereskedelmi klaszter (ábra 2-44.).
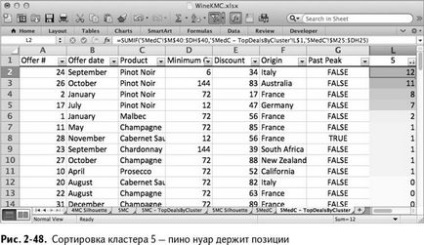
A 2. klaszter voltak vevők, akik vásárolni csak pezsgő. Champagne, prosecco és pezsgő uralják az első 11 pozíció a klaszter (ábra. 2-45). Érdekes megjegyezni, hogy a k-means megközelítés nem nagyon világosan mutatja a klaszter csillogó ventilátorok k értéke 4 vagy 5.
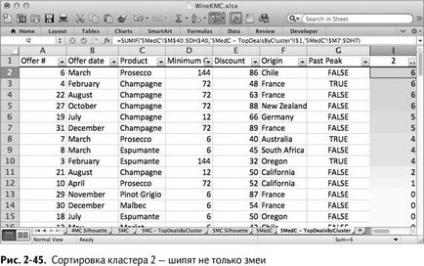
Cluster 3 - cluster Francophiles. Az öt legnagyobb foglalkozik - a francia borok (ábra 2-46.). Nem tudják, hogy kaliforniai borokat jobb?
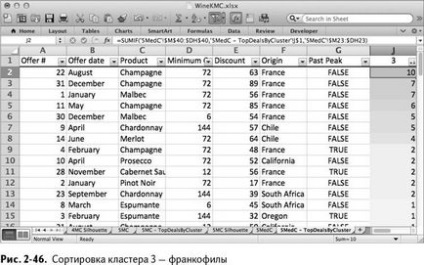
Ami a 4. klaszter, csak egy nagy dolog. És a legnépszerűbb ajánlat - egy nagy kedvezményt, és még nem telt el a maximális árat (ábra 2-47.).
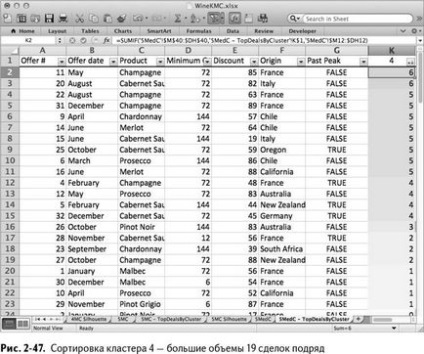
Cluster 5 ismét egy klaszter pinot noir (ábra. 2-48).
Így tisztább, nem? Ez azért van, mert az eljárás k-medián, aszimmetria indexek módszereinek alkalmazásával távolságok mérése, mint az egyenlőség koszinuszok lehetővé fürtözött ügyfelek, inkább a saját preferenciái, mint szeret. Végtére is, mi érdekli ez!
Ez az, ami képes az intézkedés a távolságot!
Most akkor a csap az öt klaszter, importálja őket vissza MailChimp.com mint egységes mező az üzenet listában, és használja ezeket az értékeket, hogy hozzanak létre a marketing forgalmazása klaszterek. Ez segít jobban vegye fel az ügyfelek és az értékesítések.