transzformációs mátrix
A transzformációs mátrix kiszámítására használjuk az új koordinátákat a tárgy során átalakulás. Változtatásával értékeit az elemek a transzformációs mátrix, lehet alkalmazni, hogy bármilyen tárgy a transzformációs (pl skálázás, flip, forgatni, mozog, stb ...). A bármelyik transzformációs tartjuk párhuzamos a tárgy.
Koordinátákat PDF lehet kifejezni kétdimenziós térben. Egy pont (x, y) a térben lehet kifejezni vektor formában [x y 1]. Állandó harmadik eleme a vektor (1) kell használni a vektor 3x3 mátrixok számítások az alábbiakban ismertetjük.
Konverzió a két koordináta-rendszer képviseli, mint egy 3x3-as mátrix, és van írva a következő:
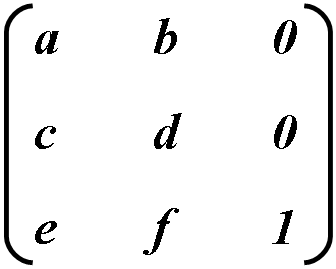
A koordináta-transzformációk formában kifejezve a mátrix szorzás:
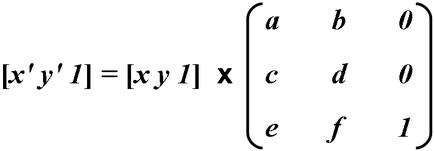
Mivel az utolsó oszlop nem nincsenek hatással a számítási eredmények, ez a számítás nem vesz részt. Koordináta transzformáció kiszámítása a következő képletek:
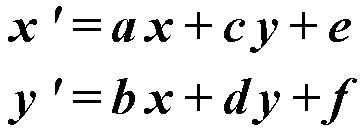
Úgynevezett identitás mátrix, hogy a mátrix, amelyben a és d értéke 1, és a többi 0. Ez a mátrix az alapértelmezett, mivel nem vezet a transzformációs. Ezért az identitás mátrix használjuk alapként.
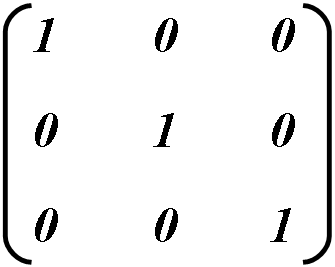
Ahhoz, hogy növelje vagy csökkentse a méret a tárgy vízszintes / függőleges változás értékét kell lennie, vagy d, illetve, és alkalmazza a többi egység mátrix.
Például: növelni a méretét az objektum kétszer vízszintesen, egy értéket kell venni, hogy 2, míg a másik, például, hogy hagyjuk a készüléket mátrixot.
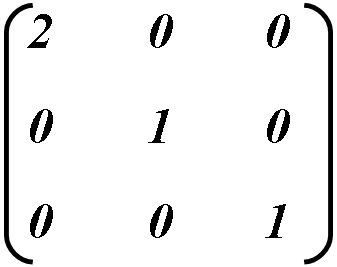
Kiszámítjuk az új objektum koordinátáinak:
Ahhoz, hogy egy tükrözés objektum vízszintes kell beállítani, hogy a = -1. Függőleges d = -1. Megváltoztatása az értékek megjelenítésére használható egyszerre mind vízszintesen, mind függőlegesen.
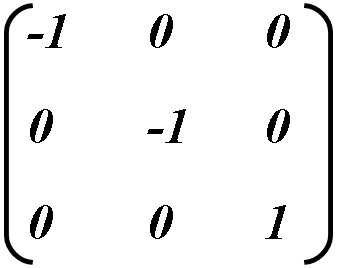
A dőlés a tárgy vízszintes / függőleges értékek módosítása, feltéve, B, illetve C. Változó értéke b / -B - dönthető fel / le, c / c - jobb / bal.
Például: billenteni függőlegesen felfelé objektum az érték beállításához b = 1
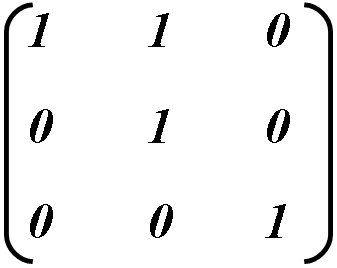
Kiszámítjuk az új objektum koordinátáinak:
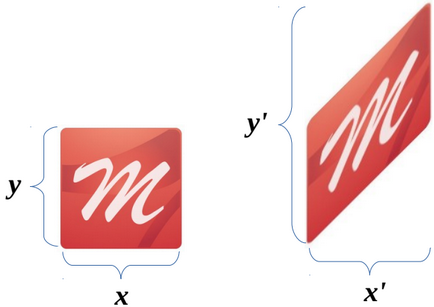
Ennek eredményeként a hajlam a tárgy hatására csak a koordináta y. amely növeljük egy x értéket.
Forgatás - kombinációja nagyítás és dönthető, de megőrizni az eredeti arányait az objektum, az átalakítás kell végezni pontos számításokat Sines és koszinuszok.
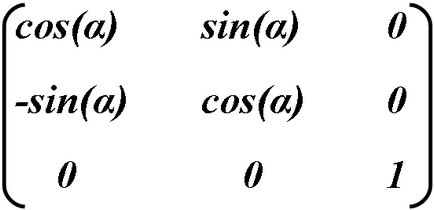
Self forgás az óramutató járásával ellentétes, α meghatározza a forgásszög fokban.
Mozgó változtatásával az E (vízszintes) és f (függőleges). Az értékek pixelben.
Például: mozgatása egy olyan mátrix felhasználásával ritkán használják annak a ténynek köszönhető, hogy ez a művelet elvégezhető más módszerekkel, például változtatni a helyzetét a tárgy a geometria lapon.
Mivel a transzformációs mátrix csak hat elem, hogy lehet változtatni, vizuálisan úgy tűnik, a PDF [a b c d e f]. Ilyen mátrix lehet bármilyen lineáris transzformáció egyik koordináta-rendszerből a másikba. Transzformációs mátrix van kialakítva az alábbiak szerint:
- Mozgások vannak feltüntetve [1 0 0 1 TX ty]. ahol tx és ty - a távolság a tengely a vízszintes és függőleges koordinátái, ill.
- Méretezés javallt [sx 0 0 sy 0 0]. Ez mérlegek koordinátáit úgy, hogy 1 egység vízszintes és függőleges méretek az új koordinátarendszerben az azonos méretű, mint sx és sy egységek a régi koordináta-rendszer volt.
- Meneteket készítünk mátrix [cosθ sinθ -sinθ cosθ 0 0]. amely megfelel a forgástengelye a koordináta-rendszer a θ fokkal balra.
- A meredekség jelzi, mint [1 tanα tanβ 1 0 0]. amely megfelel a dőlése tengely X szögben α és az y tengely által szögben β.
Az alábbi ábra példákat átalakulás. A mozgás iránya a, elfordulási szög és a Tilt, amint az ábrán látható megfelelnek a pozitív értékek a mátrix elemek.
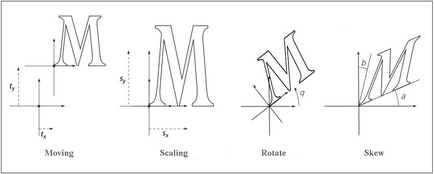
Mátrixszorzással nem kommutatív - a sorrendet, amely mátrixok szorzata, be van állítva.
Az alábbi táblázat mutatja a megengedett értékeket az átalakítás és a mátrix.