Szorzás és osztás az egészek
Ha a szorzás és osztás az egészek használják néhány szabályt. Ebben a leckében megnézzük mindegyik.
Ha a szorzás és osztás az egészek kell figyelni, hogy a jeleket a számok. Tőlük függ, hogy melyik szabály alkalmazandó. Továbbá, meg kell tanulni néhány a jogszabályok szorzás és osztás. A tanulmány ezen szabályok elkerülése érdekében néhány bosszantó hibákat a jövőben.
szorzás jogszabályok
Néhány törvények a matematika, az általunk figyelembe vett jogszabályok matematika óra. De még nem vizsgálta a törvényeket. A matematikában sok törvényt, és nem lenne bölcs dolog tanulmányozni őket sorrendben, ha szükséges.
Kezdeni, emlékezzünk mi áll szorzás. Szorzás három paraméter: a szorzó. szorzó és a termék. Vegyük például egy egyszerű kifejezés:
Itt 3 - egy szorzót, 2 - 6 tényező - a munka.
Szorzandó mutatja mi növekszik. Példánkban növeljük a 3-as szám.
A faktor jelzi, hogy hányszor, hogy növelni kell a szorzó. Példánkban a szorzó a 2-es szám Ez a tényező jelzi, hogy hányszor, hogy növelni kell a szorzót 3. Vagyis a művelet számát megszorozzák a 3 növekedni fog kétszer.
A termék - valójában az eredménye szorzás. Példánkban a termék a 6-os szám Ez a munka a termék 3-2.
Expression 3 × 2 is lehet érteni, mint az összege két triplet. A faktor 2 ebben az esetben jelenik meg, hogy mennyi idő szükséges, hogy összekapcsolják a hármas:
Kommutatív jog szorzás
Már foglalkoztunk a kommutatív törvény a szaporodás matekórán törvényeket. Nézzük ismételje meg újra.
A szorzó és a szorzó az úgynevezett közös szó - tényezők. Kommutatív törvénye szorzás az alábbiak szerint:
By permutációk tényezők helyezi a termék nem változik.
Jelölje be ezt. Szorozzuk például 3 és 5 Itt, 3. és 5., ez tényezők.
Most cserélje tényezők:
Mindkét esetben választ kapunk 15, akkor a kifejezést a 3. és 5 × 5 × 3, akkor véget egyenlőségjel, mert ugyanezt a jelentést hordozzák:
És a kommutatív törvény szorzata változók fog kinézni:
ahol a és b - a faktorok
Az asszociatív törvény szorzás
Ez a törvény azt mondja, hogy ha a kifejezés áll, számos tényező befolyásolja, a termék nem függ a teendők.
Például, 3 × 2 × 4 áll több tényező. Először szaporodnak a 2. és 3. számítani, majd a kapott terméket szorozni a maradék 4-es számú fog kinézni:
3 × 4 = 2 × (3 × 2) × 4 = 6 × 4 = 24
Ez volt az első változata a megoldás. A második lehetőség az, hogy mi lehet az első szaporodnak a 2. és 4. majd a kapott terméket kell szorozni a maradék 3-as szám fog kinézni:
3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24
Mindkét esetben megkapjuk a választ 24. Ezért kifejezések között, és ha nem tud egy egyenlőségjel, mert ugyanezt a jelentést hordozzák:
(3 × 2) × 4 = 3 × (2 × 4)
és lehet írni változók asszociatív törvény szorzás az alábbiak szerint:
a × b × c = (a × b) × c = a × (b × c)
ahol ahelyett, hogy a, b, c bármennyi lehet.
Disztributív jog szorzás
Ez a törvény megtudtuk matekórán törvényeket. Nézzük ismételje meg újra.
Disztributív jog szorzás lehetővé teszi, hogy szaporodnak az összeget a számot. E célból mindegyik kifejezés ennek az összegnek meg kell szorozni ezt a számot, és az eredmények összeadódnak.
Például, azt találjuk, a kifejezés értéke (2 + 3) × 5
Kifejezése, amely zárójelben az összege. Ezt az összeget meg kell szorozni a szám 5. Ennek érdekében minden kifejezést ezen összeg, vagyis a szám 2. és 3. meg kell szorozni 5-ös szám, és az eredmények összeadódnak:
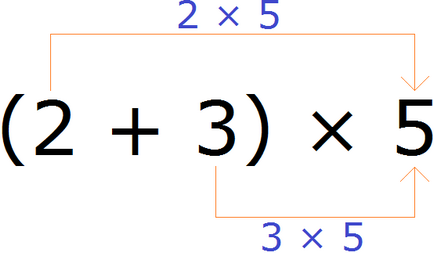
(2 + 3) × 2 = 5 × 3 + 5 × 5 = 10 + 15 = 25
Ezért az értéke expressziós (2 + 3) × 5 egyenlő 25.
A rendszer segítségével a változók elosztó jog szorzás van írva a következő:
(A + b) × c = a × c + b × c
ahol ahelyett, hogy a, b, c bármennyi lehet.
A törvény a szorzás nullával
Ez a törvény azt mondja, hogy ha bármilyen szorzás van legalább egy nulla, akkor a válasz nem érkezik a nullához. Úgy néz ki, törvény az alábbiak szerint:
A termék értéke nulla, ha legalább az egyik tényező nulla.
Például, a kifejezés 0 × 2 nulla
Ez felveti a kérdést: „miért?”. Ebben az esetben, az ördögbe olyan tényező, és azt mutatja, hogy hányszor kell növelni a szorzót. Ez azt jelenti, hogy hányszor zéró növekedést. Szó szerint, ez a kifejezés értelmezése: „zéró növekedés kétszer.” De hogyan lehet növelni a nulla kétszer, ha az nulla?
Más szóval, ha a „semmi” a kettős vagy akár egy millió alkalommal, akkor még mindig a „semmi”.
Ha a kifejezés 0 × 2 cserélhetők tényezők, ismét kap nulla. Ezt tudjuk az előző kommutatív törvény:
Példák a jog alkalmazását a szorzás nullával:
× 2 5 × 0 × 9 × 1 = 0
Az utolsó két példa, számos olyan tényező van. Látva őket nulla, akkor azonnal fel nullát a válasz, a törvény a szorzás nulla.
Mi borított alaptörvényei szorzás. Ezután úgy a szorzás az egész számok.
Szorzás egészek
1. példa: Find expressziós -5 × 2
A szorzás a számok a különböző jeleket. -5 egy negatív szám, és 2 - pozitív. Ilyen esetekben meg kell alkalmazni a következő szabály:
Ahhoz, hogy szaporodnak a számos különböző karakter, szükséges, hogy szaporodnak a modulok előtt, és a kapott választ a mínusz jel.
-5 × 2 = - (| -5 | × | 2 |) = - (5 × 2) = - (10) = -10
Általában rövidebb rögzített: -5 × 2 = -10
Ez felveti a kérdést: „miért?” A tény az, hogy minden szorzás felírható a számok összege. Vegyük például a véleménynyilvánítás 2 × 3. egyenlő 6.
A tényező ez a kifejezés a 3-as szám Ez a tényező jelzi, hogy hányszor, hogy növelni kell a kettő. De a kifejezés 2 × 3 is kifejezett összege három diád:
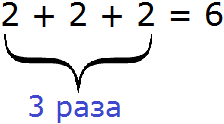
Ugyanez történik a kifejezés -5 × 2 Ez a kifejezés is képviselteti magát egy bizonyos összeget
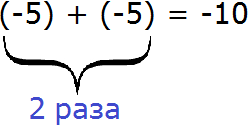
És a kifejezést (5) + (-5) értéke -10, és tudjuk, hogy a korábbi leckéket. Ez a kiegészítés a negatív számok. Emlékezzünk, hogy az eredmény a hozzáadott negatív számok egy negatív szám.
2. példa Find expresszióját 12 × (-5)
A szorzás a számok a különböző jeleket. 12 - egy pozitív szám, (5) - a negatív. Ismét alkalmazni az előző szabályt. Szorozzuk meg a számok és mértékegységek a választ, hogy egy mínusz jel:
× 12 (-5) = - (| 12 | × | -5 |) = - (12 × 5) = - (60) = -60
Általában, rövidebb írási: 12 × (-5) = -60
3. példa Find értékét expressziós 10 × (-4) × 2
Ezt a kifejezést az számos tényezőtől. Először is, szaporodnak 10, és (4), majd megszorozzuk a kapott számot 2. Egyébként a korábban megtanult szabályokat kell alkalmazni:
10 × (-4) = - (| 10 | × | -4 |) = - (10 × 4) = (-40) = -40
-40 × 2 = - (| -40 | × | 2 |) = - (40 × 2) = - (80) = -80
Ezért az expressziós 10 × (-4) × 2 -80
Általában, rövidebb írási: 10 × (-4) × 2 = -40 × -80 = 2
4. példa Find a kifejezés értéke (-4) × (-2)
A szorzás a negatív számok. Ilyen esetekben meg kell alkalmazni a következő szabály:
Ahhoz, hogy szaporodnak negatív szám, meg kell szaporodnak a modulok előtt és választ kapott, hogy egy plusz jel
(-4) × (-2) = | -4 | × | -2 | = 4 × 2 = 8
Plus hagyományosan nem írok, úgyhogy csak annyit írj a választ 8.
Általában rövidebb rögzített (-4) × (-2) = 8
Felmerül a kérdés, hogy miért a szorzata negatív számok hirtelen kap egy pozitív számot. Próbáljuk bizonyítani, hogy (-4) × (-2) értéke 8 és nem valami mást.
Először is, mi írjuk a következő kifejezést:
Azt zárójelek:
Add, hogy ez a kifejezés a mi kifejeződő (-4) × (-2). Ő is van zárójelben:
Mindez nullának:
Most kezdődik a móka. A lényeg az, hogy ki kell számolnunk a bal oldali ezt a kifejezést, és ennek eredményeként, hogy egy 0.
Így, az első termék (4 × (-2)) egyenlő -8. Írunk a kifejezések száma a mi -8 helyett a termék (4 × (-2))
Most ahelyett, hogy a második termék kínálat átmenetileg ellipszis
Most alaposan nézd meg a kifejeződése -8 + [...] = 0. Melyik számot kell jönni helyett pontokat egalitárius? A válasz nyilvánvaló. Ahelyett, hogy pont legyen egy pozitív számot 8 és nem több. Csak ezen a módon fogják tartani az egyenlőség. Miután -8 8 + 0.
Visszatérve az expressziós -8 + ((-4) × (-2)) = 0, és ehelyett a munka ((-4) × (-2)) rekord számú 8
5. példa Find expressziós -2 × (6 + 4)
Alkalmazzuk a disztributív törvény szorzás, azaz szaporodnak száma -2 szereplő kifejezések az összeg (6 + 4)
-2 × (6 + 4) = (-2 × 6) + (-2 × 4)
Most számítani kifejezést zárójelben vannak. Ezután adjuk hozzá az eredményeket. Az út során, alkalmazza a korábban megtanult szabályokat. Entry modulokat el lehet hagyni, így nem terhelik feleslegesen a kifejezést
-2 × 6 = - (2 × 6) = - (12) = -12
-2 × 4 = - (2 × 4) = - (8) = -8
Ezért az expressziós -2 × (4 + 6) van -20
Általában rövidebb rögzített: -2 × (6 + 4) = (-12) + (-8) = -20
6. példa Find expresszióját (-2) × (-3) × (-4)
A kifejezés áll több tényező. Először, megszorozzuk száma -2 és -3, és a terméket szaporodnak a maradék számot -4. Írásban modulok hiányzik, így nem terhelik feleslegesen a kifejezést
Ezért az értéke expressziós (-2) × (-3) × (-4) egyenlő -24
Általában rövidebb rögzített: (-2) × (-3) × (-4) = 6 × (-4) = -24
osztály törvények
Mielőtt osztani egész, meg kell vizsgálni a két hadosztály a törvény.
Először is, ne feledjük, hogy mi van a szétválás. Az osztály három paraméter: az osztalék. osztó és hányadosa. Vegyük például egy egyszerű kifejezés:
Íme 8 - az osztalék, 2 - 4 térelválasztó - magán.
Osztalék mutatja, hogy mi osztjuk. A mi példánkban ossza száma 8.
Elválasztó azt mutatja, hány részből kell osztani az osztalékot. Példánkban az osztó száma 2. Ez osztó megmutatja, hogy hány részből kell osztani az osztalék 8. Azaz során szétválás működés, a 8-as számú oszlik két részre.
Self - valójában az eredménye egy osztás. Példánkban a megadott szám 4. Ez hányadost úgy kapjuk meg 2 8.
Ezután úgy a szétválás a törvényeket.
Zero nem osztható
Bármennyi osztva nulla tilos. Ez felveti a kérdést: „miért?”.
Az a tény, hogy ez a felosztás az inverz művelet szorzás. Például, ha a 2 × 6 = 12, akkor 12. 6 = 2
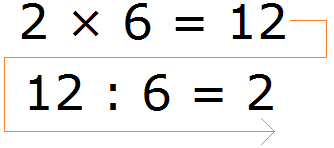
Látható, hogy a második expressziós van írva fordított sorrendben.
Most ugyanezt a kifejezést 5 × 0. tudjuk a szorzás a törvények, hogy a termék értéke nulla, ha legalább az egyik tényező nulla. Ezért az expressziós 5 × 0 nulla
Ha írunk ezt a fordított sorrendben, megkapjuk:
Megragadja a szemet választ 5 amelyek úgy kapjuk meg, a nulla nullára. Lehetetlen és ostoba.
A fordított is írt egy másik hasonló kifejezést, például, 2 × 0 = 0
Az első esetben, elosztjuk nulla nulla, van 5 és a második esetben 2 Azaz, minden egyes alkalommal, elosztjuk nulla nulla, akkor kap a különböző értékeket, és ez elfogadhatatlan a matematikában.
Ez volt az első magyarázat, hogy miért nem lehet nullával osztani.
Egy másik magyarázat az, hogy az osztalék osztva az osztó találni egy számot, megszorozva az osztó ad osztalékot.
Például a kifejezés 8. 2 találni egy számot, amely ha kell szorozni 2 ad 8
Itt helyett a dot számot kell megadni, amely ha megszorozzák 2 ad választ 8. Ahhoz, hogy megtalálja ezt a számot, ez elegendő ahhoz, hogy ezt rögzíti a fordított sorrendben:
Most képzeljük el, hogy meg kell találni a kifejezés értéke 5. 0. Ebben az esetben az 5. - az osztalék, 0 - térelválasztó. Szakasz 5-0 azt jelenti, hogy talál egy számot megszorozva 0 5 képet
Itt két pont helyett a számnak kell lennie, amely megszorozva 0 megadja a választ 5. De nincs olyan szám, amely megszorozva 5 ad nulla.
Expressziója [...] × 0 = 5 törvénye ellen szorzás nullával, amely azt állítja, hogy a termék egyenlő nullával, ha legalább az egyik olyan tényező nulla.
Így írja le a kifejezés [...] × 0 = 5 fordított sorrendben, elosztjuk 5-0 nincs értelme. Ezért mondják, hogy nem lehet nullával osztani.
Ezzel a törvény változó van írva a következő:
Ez a kifejezés a következőképpen módosul:
Számos osztható száma b. azzal a megkötéssel, hogy b értéke nem nulla.
Ez a törvény azt mondja, hogy ha az osztalék és az osztó szorzata vagy hányadosa ugyanazt a számot, a hányados nem változik.
Vegyük például az expressziós 12. 4. Ennek értéke kifejezés egyenlő 3
Próbáljuk szaporodnak az osztalék és Divisor hogy ugyanazt a számot, mint például a több 4. Ha úgy gondolja, a magántulajdon, akkor vissza kell mennie a válasz 3. számú
(12 × 4). (4 × 4)
(12 × 4). (4 × 4) = 48. 16 = 3
3. kapott választ.
Most próbáld meg nem szaporodnak, és felosztják a jelenséget és osztó száma 4
(12. 4). (4. 4)
(12. 4). (4. 4) = 3. 1 = 3
3. kapott választ.
Látjuk, hogy ha az osztalék és az osztó szorzata vagy hányadosa ugyanazt a számot, a hányados nem változik.
Megvizsgáltuk két hadosztály a törvény. Ezután úgy az osztás az egész számok.
Az osztás az egészek
1. példa: Find expressziós 12 (-2)
Ez a felosztás a számok a különböző jeleket. 12 - egy pozitív szám (-2) - negatív. Ilyen esetekben szükség van egy modul az osztalék osztva az elválasztó egység, és a válasz egy mínusz jelet.
Általában rögzített rövidebb 12. (-2) = -6
Példa 2. Keresse meg az egy kifejezés értékét -24. 6
Ez a felosztás a számok a különböző jeleket. -24 - ez egy negatív szám, 6 - pozitív. Ezekben az esetekben, újra meg kell egy modult az osztalék osztva az elválasztó egység, és a válasz egy mínusz jelet.
Általában rövidebb írási -24. 6 = -4
Példa 3. Keresse meg a kifejezés értéke (-45). (-5)
Ez az osztály a negatív számok. Ilyen esetekben szükség van egy modul az osztalék osztva az elválasztó egység, és a válasz egy plusz jel.
(-45). (-5) = | -45 |. | -5 | = 45. = 5 9
Általában rögzített rövidebb (-45). (-5) = 9
4. példa Find a kifejezés értéke (-36). (-4). (-3)
Rendje szerint a cselekvés. ha a kifejezés csak akkor van jelen szorzás vagy osztás, akkor az összes végrehajtandó műveletek balról jobbra sorrendben jelennek meg.
Osszuk (-36) a (-4), és az így kapott számot elosztjuk (-3)
(-36). (-4) = | -36 |. | -4 | = 36. 4 = 9
Általában rögzített rövidebb (-36). (-4). (-3) = 9. (-3) = -3
Mint a leckét?
Csatlakozzon az új csoport Vkontakte és értesítéseket kapni az új órák