Legrövidebb út probléma két pont között
A hossza a legrövidebb út .... Mozgó a kezdetektől vertex, hogy a végén a kijelölt élek szerezni a legrövidebb utat.
3. A feladat meghatározása a maximális áramlási
Úgy véljük, egy hálózat, egy bemeneti csomópontot (forrás) és egy kimeneti csomópont (drain). Határozzuk meg a maximális érték a fluxus (gépek számát, az üzenetek, folyadék, stb), ami megköti a villamosenergia-rendszer és a belőle egy adott időszakon belül. Feltételezzük, hogy a szennyvíz a csomópont megegyezik a fluxus áramlik a csomópont.
Sávszélesség (vagy teljesítmény) az ív - a felső határt az áramlás az ív. Például, autópályák korlátozzák a járművek száma a közlekedési rendszer a csővezetékek érték korlátozza az olaj mennyisége a forgalmazási rendszerben.
Áramfolyás függhet annak irányát.
Ez a szimbólum azt jelzi, hogy a villamosenergia-áramlás a 1 csomópont a 2 csomópontra egyenlő 6, és a villamosenergia-áramlás a 2 csomópont a csomóponthoz 1 értéke 0, azaz, Ez a „egyirányú utca”.
Ez azt jelenti, hogy a villamosenergia-áramlás minden irányban egyenlő 2.
Feltesszük, a kívánt értéket a maximális áramlási nullával egyenlő.
1. lépés valamilyen módon a forrástól a lefolyó, amely által alkotott ívek, amelyek mindegyike egy nem nulla teljesítményt áramlási irány. Ha egy ilyen utat nincs jelen, akkor az optimális megoldást nem találnak.
2. lépés: Keresse meg a legkisebb teljesítmény értéke Pf ív a kiválasztott útvonal 1. lépésben növeli az áramlás a hálózaton keresztül az értékét Pf.
3. lépés: az úton a 1. lépésben, hogy csökkentsék az áramlás, összes ívben Pf az áramlás irányában, és növeli a teljesítmény Pf áramlik minden ívek az ellenkező irányba. Ugorjon 1.
Példa. A rendszer az utak „Észak-Dél” áthaladó Pskov régió rendelkezhetnek sávszélességeket reakcióvázlaton látható (th. Cars per óra).
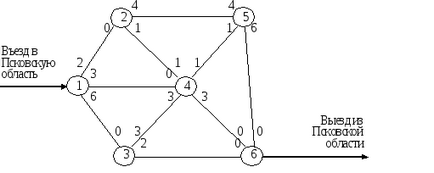
Határozzuk meg a maximális áramlási a rendszeren keresztül (thous. Cars per óra).
A kívánt érték a maximális áramlás értékét nullára.
Iteration 1. Válassza ki az utat
Pf = min = .... Ezért, az energiaáramlásokra ......... utat az áramlás irányában (azaz, ... és ...) mennyiségének csökkentése Pf = ..., és az energiaáramlásokra fordított irányban az utat .......... (... és ...) nőtt Pf = .... A teljes áramlás
Iteráció 2. Jelölje ki a görbét
Pf = min = .... Minden áramlások a görbét ......... általános áramlási irány (... és ...), hogy csökkentse a Pf = ..., és az összes áramlás ilyen módon a fordított irányban (... és ...) növekszik Pf = .... A teljes áramlási növekszik Pf = ... (............).
Iteration 3. Válassza az utat
Pf = min = .... Minden stream az úton .......... az általános áramlási irány (.............), hogy csökkentse a Pf = ..., és az összes áramlás ilyen módon a fordított irányban (............) növekszik Pf = .... A teljes áramlási növekszik Pf = ... (................).
Iteration 4. Válassza az utat
Pf = min = .... Az összes szál az úton ................ az általános áramlási irány (............... ..), hogy csökkentse Pf = ..., és az összes áramlás ilyen módon a fordított irányban (............... ..), hogy növelje Pf = .... A teljes áramlási növekszik Pf = ... (............ ..).
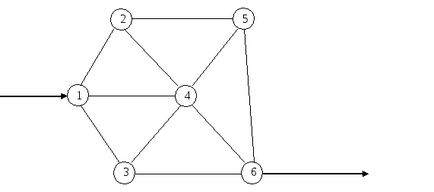
Iteráció 5. Válassza az utat
Pf = min = .... Az összes szál az úton ................... az általános áramlási irány (.................. ..), hogy csökkentse Pf = ..., és az összes áramlás ilyen módon a fordított irányban (.................. ..), hogy növelje Pf = .... A teljes áramlási növekszik Pf = ... (.............).
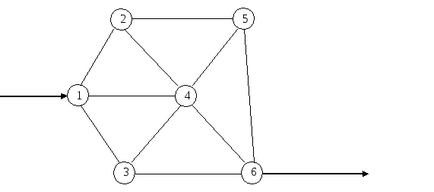
Létezik többé utak csomópontból 1 6 csomópont kapacitást meghaladó nulla egészen. Következésképpen .... ezer -. a maximális áramlás a hálózaton keresztül.
Határozza meg a nagyságát és az áramlási irányt minden ív. Az áramlás iránya megfelel a kiválasztott utakat. A légáram áthalad egy íven keresztül, amelynek értéke egyenlő a különbség a kezdeti és a végső áramlási kapacitás:
ív 1-2: kezdeti erő ... (az eredeti gráfban), végleges - ... (az utolsó oszlop), úgy, hogy egy olyan irányban, 1 csomópontnak a 2 csomópontra áramlási kapacitása
Ennek eredményeként, kapunk egy grafikon, ami azt jelezte, az irányt és a teljesítmény áramlást mindegyik ív: