Ahol építeni grafikonok a logaritmikus jellemzőinek egy nyitott rendszer, MATLAB

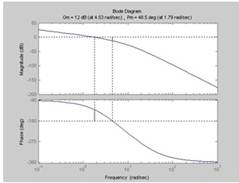
Építsd grafikonokat logaritmikus jellemzői a nyílt hurkú rendszer MATLAB (Bode tőke vagy üzemeltető) Fig. Valamint 1.3.

Mi telek APFC MATLAB (nyquist operátor) Fig. 1.3 b a nyílt hurkú rendszer.

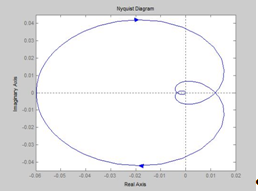
Stabilitás árrés nagyság és fázis által meghatározott logaritmikus jellemzők (lásd az 1.3 ábrát a ..) a WC-levágási frekvenciát határozza meg fázistöbblet - # 8710; # 966;, és az amplitúdó árrés # 8710; L - a frekvencia, amelyen # 966; (w) = -180. Így # 8710; L≈0. 1dB, # 8710; # 966; ≈ 0 °, ami nem megfelelő.

4. Az nagysága a sebesség hiba definíciója esk = V1 / K. Durva becslés és TPP # 963; kell építeni tranziens h (t) (lépése szereplő MATLAB) ha v (t) = 1 [t], és meghatározza rajta és a TPP # 963;.

A normál állapotban egyenletek formájában a differenciálegyenlet zárt rendszer

D (k) y (t) = a Kv (t). Ha D (k) = b0s4 + b1s3 + b2s2 + B3s + B4 = 0. az állam egyenlet formájában

A leírás, dinamikus rendszerek állapottér Matlabban alkalmazni ss alosztály modelleket, amelyek alapján lineáris differenciál vagy differenciaegyenletek.

rendszer folyamatos modell ss alosztály a formája:

ahol: x - az állapot vektor; V- bemenet vektor; y - kimeneti vektor.

A formáció a minták a alosztályba ss ss tervezett funkció

Ennek eredményeként néven sys szerezni ss-objektumot numerikus jellemzők formájában négy mátrixok, amelyek egyeztetni kell méretét. D mátrix ebben az esetben egyenlő 0.

A konstrukció az átmenet folyamata h (t) használja a kezelő lépés MATLAB.

Megvalósítása funkciók a következők:

sys = ss ([0 1 0 0, 0 0 1 0, 0 0 0 1; -b4 / B0 -B3 / B0 -b2 / B0 -b 1 / B0], [0 0 0 K / b0]”, szem ( 4), nullákat (4,1))

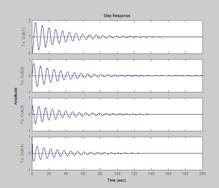
Ennek eredményeként, megkapjuk a grafikonok ábrán látható. 1.4. Mi budetinteresovat Out (l). fordulatszám hiba érték meghatározása a következő:

EKKR = V1 / K = 1,4 / 3243 = 0,432> eskzad = 0,04.

Durva becslés TNN és ​​építsen egy átmeneti folyamat h

A átmeneti folyamat alapján határozzák meg a következő arányok: # 949; száj = v (t) / (l + K), ahol V (t) = l [t], és a K = 3243 - a teljes nyitott hurkú átviteli koefficienst. Ezután eust = 1 / (1 + 3,243) = 0,236, és ezért a gráf TPP OUT (L) TPP ≈50s> tppzad = 2.5kivéve.

Így, az eredeti rendszer nem felel meg az előre meghatározott minőségi mutatók, meg kell javítani.

5. Ha a forrás rendszer nem felel meg az előre meghatározott minőségi mutatók, meg kell javítani. Kívánt LACHH lzh (w) van kialakítva alkalmazó frekvencia korrekció szintézis módszerek. Az alacsony frekvenciájú tartományát, miközben a kívánt LACHH sorrendben astatism (jelenlétében integrátor 1 / s a ​​rendszerben) kiválasztja a kívánt erősítés arányából Kz = v1 / ESK = 1,4 / 0,04 = 35. A levágási frekvencia LACHH kívánatos, hogy a lejtőn a -20 dB / évtizedben hossza ezen része nem kevesebb, mint egy évtized alatt. További midrange LACHH része illeszkedik a kisfrekvenciás vonalszakasz meredekség -40 (ha szükséges -60) dB / évtizedben, és a nagyfrekvenciás része a kívánt forrás és egybe kell esniük LACHH véletlenül.

Mivel a minőségi követelményeket az átmeneti folyamat: TPP és # 963;, a stabilitás állományok figyelembe venni, amikor alkotó középtartományban lzh (w). Itt, a diagramon (ábra. 1.5).

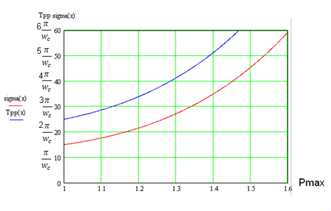
Szerint a ábra grafikonja. 1.5 előre meghatározott értékek TNN és ​​megtalálni Wp, majd a kapcsolat wc = (0,6-0,9) Wt. Levágási frekvencia wc.

A mi esetünkben (amint azt a 1.5 ábra) az y = 10%, TP = 3π / # 969; n, ahol tp értéke # 969; p = 3π / 1,5 = 6,8 1 / s és # 969; c = 1 májusi / s.

Konjugáció középrészének alacsony frekvenciájú és nagy frekvenciájú (ábra. 1.6) kell lennie, hogy könnyebb volt megtörését és a korrekció, ha lehetséges, nem lehet több, mint 20 dB / évtizedben (hengeres rész hossza körülbelül tíz nap). Ezután válasszuk ki a frekvencia L2≈10dB # 969; 2 = (0,1-0,5) # 969; c = 2,5<ωс=5 и L3≈ -10 дБ на частоте ω3=25 ≥ ωс=5. Введем обозначения:

érték # 969; 1 talált a feltétele az egyenlőség lzh értékek (# 969, 1) = Liskh (# 969, 1). ezt

kapcsolatban vezet a következő kifejezést:

Az utolsó kifejezés jelzi:

Az utolsó két érték a kifejezés a Liskh (w).

Az érték a következő képlettel # 969; 1 = 0,098

LACHH korrekciós eszköz a jellegzetes Lk (w) felel meg, a függvény:

A teljes átviteli függvénye a nyílt hurkú rendszer egy korrekciós eleme a szekvenciális típus a következő:

Ezután használjuk a funkciót zpk (z, p), ahol z és p - vektor nullák és oszlopok, a Kd - egy általános áttétel, sys - bármilyen nevet rendelt a modell. Ezután vegye fel a Matlab rendszerben valósul meg:

SYS1 = zpk ([- 1 / T2K -1 / t3k], [0 -1 / T1 -1 / t2 -1 / t3 -1 / t1k -1 / T4K], kd)

s (s + 7,143) (S + 4,167) (S + 25) (S + 0,4762) (S + 0,097)