A végrehajtási sorrendjét a számítás típusát
Határozat. Bemutatjuk lineáris helyettesítési (5.8) és a választott C1 = 0, h1 = 0,5; C2 = 0,10, h2 = 10 -2.
Mi a becslést a várakozások szerint az (3-7).
Elfogulatlan variancia becslése a általános képletű (3,8).
Kiszámítása kovariancia becslés hordozzák a általános képletű (5,9).
Az értékelés a korrelációs együttható a képletű (5.10).
Szelektív lineáris regressziós egyenlet Y H.
.
vagy y - 0,0978 = - 0,00678 (x + 0278).
Szelektív lineáris regressziós egyenlet Y. X
.
vagy y - 0,0978 = - 0,0122 (x + 0278).
Regressziós egyenes ábrán látható. 1, ott jelennek meg a kísérleti pontokat.
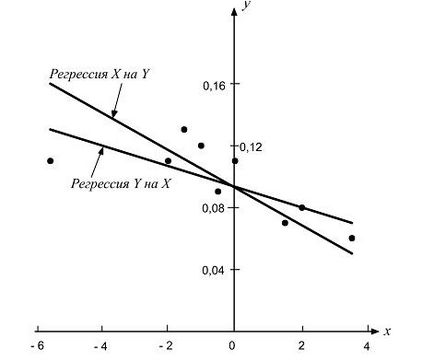
Ábra. 1. A függőség a nitrogén koncentrációja az acél (y)
kimeneténél a konverter a kezdeti szén-koncentráció (x)
By nomogramok (lásd ábra alkalmazás P1 [1] ..) értékek R = - 0746 (n = 9) találunk az intervallum: - 0,95 <ρ <– 0,14. Так как значение ρ = 0 не принадлежит найденному доверительному интервалу, гипотеза о существовании линейной зависимости не противоречит экспериментальным данным с уровнем значимости α = 0,05.
Mi ellenőrizze a hipotézist nem között lineáris összefüggés értékek X és Y segítségével a kritérium (5.13). A Student eloszlás táblázat kvantilisokat találják t0,975 (7) = 2,365. kiszámítjuk
.
Mivel | r | = 0,746> 0,667, elfogadjuk azt a hipotézist, hogy létezik egy lineáris összefüggés van a változók X és Y
A kapott eredmények alapján levonható a következtetés, hogy a növekvő mennyiségű, azonos átlagos értéke a többi érték csökken. Mivel a korrelációs együttható jelentős, azt lehet használni az egyenleteket regressziós egyenesek szelektív becslés átlagos értéke egy változó egy másik értéket.
A jelentés a szokásos számítási be kell nyújtani minden számítás, egyenlet minta regressziós egyenest. A rajzot kell benyújtani közvetlen regressziós egyenlet ugyanazt viseli az összes kísérleti pontokat. A következtetések megfogalmazására a vizsgálatának eredményéről a hipotézist jelenlétében (hiánya) a lineáris összefüggés valószínűségi változók. Ha a hipotézist a jelenléte lineáris kapcsolat, következtetést levonni a szilárdsága és a természet közötti kapcsolat az értékek X és Y.
A pontosság számítás a várakozás értékelések - váltakozó jel összehasonlítva az eredeti adatokat, becsléseket variancia, szórás, kovariancia - három szignifikáns adatot, a becsült korrelációs együttható - három tizedes.
Az, hogy a teljesítmény:
1. Számítsuk ki a becslést a várható valószínűségi változók X1 és X2. értékelési elemeket a kovariancia mátrix: varianciák és kovarianciák. Egyszerűsítése érdekében a számítás és ellenőrzés a szervezet ajánlott elvégezni a kódolás, ahogy ez 10.3. számítási szabályozás biztosítja megismételve a számítás az egyéb elveivel referencia. Az eredményeket meg kell egyeznie, hogy a kerekítési hiba.
2. Számítsuk ki a becslést a korrelációs együttható.
3. A nomogramot ([1], 83. oldal), keresse meg a megbízhatósági intervallum a korrelációs együttható, hogy teszteljék a hipotézist, hogy létezik egy lineáris összefüggés van az X1 és X2.
4. Keresse meg az egyenlet empirikus regressziós vonalak X2 X1 és X2 X1. Ahhoz, hogy épít ezeket a sorokat ugyanabban a rajzban. Ugyanezen a grafikonon alkalmaz kísérleti pontokat.
5. Győződjön meg a következtetés ereje és jellege közötti kapcsolat X1 X2.
1. Karasev VA Rumshinsky LZ Kísérlet szervezet. -M. MISA 1986 N105, str.74-78.