Tárgy henger keresztmetszete síkban
Magyarázata Epure.
Attól függően, hogy a helyzet a metsző síkban és a függőleges kerék-henger üvöltés, szekcionált ábra lehetnek:
1. kör (normál rész), ha a vágási sík merőleges a forgástengely tsilindra.
2. Az ellipszis, ha a vágási sík hajlik a henger tengelye körül forog.
3. téglalap ha metsző síkkal párhuzamos forgástengely a henger.
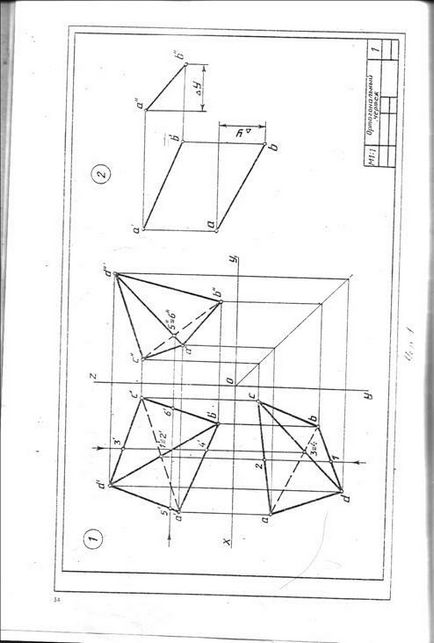
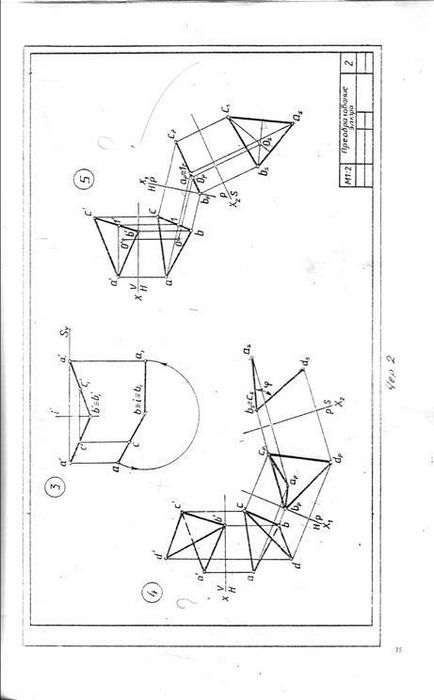
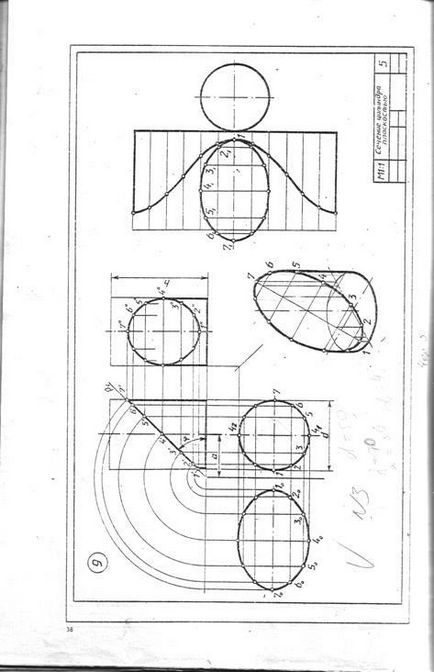
A minta és a probléma № 9 jelentése egy köralakú Qi-henger és kiálló frontálisan síkban P. ábra részben ellipszis, a vízszintes vetülete amely egybeesik odnoimen távú vetülete a henger - egy kört, és az első - jelentése szegmens 1'-7 „az első pályán pv. A pontok 1 „és a 7” koromtól rendre a legalacsonyabb és legmagasabb metszéspontja a sorban, és mindkét végét a nagytengely. Rámutat 41, illetve 42, a közeli-nyakkal és legkülső síkjához képest a sor V keresztezési pontokat és végződik ugyanabban az időben a kis tengelye az ellipszis. Köztes pont 2., 3., 5. és 6. kell építeni egy profil keresztmetszetében a vetítés számadatok-CIÓ és meghatározni a valódi érték. A helyzet a vízszintes kiálló pontok által meghatározott elosztjuk 12 egyenlő részeit a kerületén, amelybe a henger az előrejelzések, és a helyzet az első és a profil előrejelzések - útján kommunikációs vonalak. Az igazi érték a keresztmetszet alakja talált körüli forgása a vízszintes nyoma a gépet PH. t. e. merőleges tengely körül, hogy a frontális síkban egybeeső kiemelkedések és a fő nézet, amikor a következő P síkban. A konstrukciók nyilak.
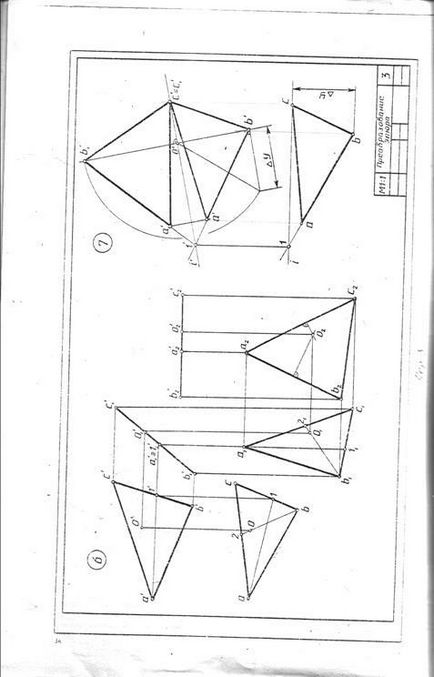
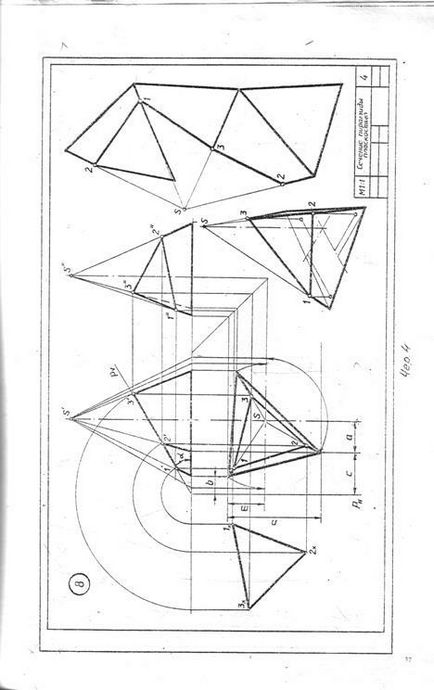
Létrehozása a felület vizsgálata egy csonkított részét a hengert a képet letapogató indul teljes oldalirányú felületén, amely előre-höz egy téglalap. Az alap a téglalap van osztva az azonos számú egyenlő részre osztva amely oszlik a henger kerületének bázis, ebben az esetben a 12. Keresztül a Division pontokat végezzük a vékony vonalak, generátorok, amelyek szekvenciális késleltetésére Z koordinátáinak pontok metszéspontja vonal. A kapott pontokat összekötve egy sima görbe mintákat. Beolvasásához leparkolt oldalsó felület alakja és keresztmetszete alapján.
Csonkolt perspektivikus nézete a henger által épített koordinátákat egymás át metszéspontjait vonalak orto-átlós nyúlványok. Erre a Z tengely egybeesik a henger tengelye, a kezdete egy - a központ az alap és épít axonometrikus vetületét a bázis (ovális izometrikus). X-tengely közötti távolság vízszintes vetülete az akkordok 22, 33, stb vett pont 1 ..; merőlegesek emelje fel a kereszteződés a tengelye az ellipszis 1-7. Keresztül minden ponton kapott lefolytatása akkord merőleges ez a fájdalom-nagytengely és a tengellyel párhuzamos OY és axonometrikus elhalasztja távolságok nekik, vesszük, hogy a vízszintes vetülete formák SE-cheniya. A kapott pontokat összekötve egy sima görbe. Vannak más nyílt forráskódú szoftverek Søby épület perspektivikusan a csonka forgástest.
Utasítások elvégzésére a diagram.
1. Végezze el kell kezdeni rajz rajz egy folytonos vékony-mi első három sora a formában a vágási sík.
Amikor összekötő lemez kell jegyezni, hogy a rajz devel-vatsya balra.
A rajzon fel kell tüntetni a szükséges pontokat, és hogy mentse-Kutató Intézet építése.
Ahelyett, hogy a szó szerinti paramétereket kell alkalmazni, hogy a méret a lehetőséget.
5. Amikor dolgozik sablonokat kell találni a helyszínen, hogy nem olvad, de a három pontot összekötő, de ez szükségessé válik csak két további lépéseket a mintát. Ezzel a módszerrel lesz elérni sima íveket.
6. Minden vetítés adatok rávilágítanak részén árnyékoló vagy árnyékban Lee Bo-színtelítettségűre.
A mintákat végre diagramok.
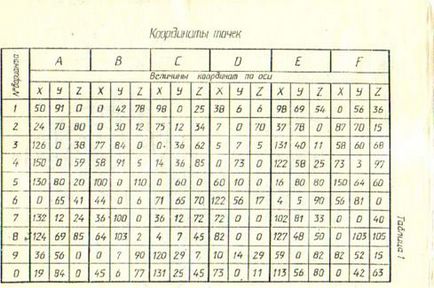
Pontok koordinátáinak (táblázat №1)
1. Bubennikov AV ábrázoló geometria. M. Higher School 1985.
2. Bubennikov AV ábrázoló geometria. Feladatok gyakorlat. - M.; Magasabb SQA la 1981.
3. Vinogradov VN ábrázoló geometria. - M. Oktatási 1989.
4. Glazunov EA Chetverukhin NF axonometria - M. Gostekhizdat 1954.
5. Gordon 8. O. Sementsov-Ogievskii MA kurzus ábrázoló geometria. - M. P. matgiz-1971.
6. Dobryakov AI során ábrázoló geometria. - Leningrad Gosstroiizdat 1952.
7. Kotov II ábrázoló geometria. - Moszkva magasabb Iskola 1969.
8. Kuznyecov NS Ábrázoló geometria. - Moszkva magasabb Iskola 1931.
9. A tantárgy ábrázoló geometria (nem habcsók PC). Szerkesztette: M. Tevlina. - M. magasságú Shaya Iskola 1983.
10. ábrázoló geometria. Szerkesztette Krylov NN - Moszkva magasabb Iskola 1984.
11. NL Russkevich Leíró geometria. - Kiev: Vishcha Iskola 1978.
12. Timrot ES Leíró geometria. - M. Stroyizdat 1962.
13. Frolov, S. A. Leíró geometria. - M. Engineering 1983.
14. Savenkov MG Mustaeva VA Ábrázoló geometria és a perspektíva. Módszertani útmutató a tanfolyamra. - Magnyitogorszk 1989.
Kinyomtatott és aláírt _______. Format 60x90 1/16
Headset Times New Roman Cyr, 10. adat. Pec. lapot. - ___. W., ed. - ___.
Licenc №172 származó 12.09.96, a