Racionális számok és időszakos tizedessel
(Tipp: A kapott eredmények oldalakon 31 - 33.).
Racionális számokat p q. amely nem ábrázolható
véges tizedessel bomlanak végtelen tizedes tört egy közönséges vétel „hosszú” osztály. Minden szakaszban a ez a folyamat maradékot nem egyenlő nullával, egyébként várható lett volna a végső frakciót. Különböző előforduló maradékokat csak egész számok 1 q - 1, és így már csak q - 1 lehetőségeit értékeit ezek a maradványok. Ez azt jelenti, hogy egy bizonyos szétválására q k a fennmaradó lesz a második alkalommal. De aztán az összes alábbi egyenlegek is ismétlődik ugyanabban a sorrendben, amelyben megjelent első előfordulása után a maradék k. Így
tizedes bővítése minden racionális szám az a tulajdonsága, rendszeresség; egy bizonyos számú tizedesjegy jelentése azonos csoportba a tizedesjegy kezd ismételni végtelen számú alkalommal. Például, június 1-én = 0,166666666. ; Július 1 = ,142857142857142857. ;
Január 11 = 0,09090909. ; 1100 122 = 0,1109090909. ; 11 90 = 0,122222222. és így tovább. d. (Megjegyzés: a racionális számok jelennek meg
egy véges decimális, hogy ez az utolsó frakció lehet képzelni, után utolsó tizedes helyen végtelenségig megismételve a számjegy 0, és így, nézett racionális számok nincsenek kizárva ezt a fenti általános készítményt.) Ezek a példák azt mutatják, hogy néhány decimális bővítések megfelelő racionális számok, időszakos „farok” előzi meg nem periodikus „fej”.
Ezzel szemben nem lehet bizonyítani, hogy minden periodikus frakció racionális számok. Vegyük például, egy végtelen időszakos frakciót
Mi lehet írni: p = 100 + 33 · 10 -3 2 (1 + 10 -1 + 10 -2 +.). kifejezést

§ 2NESOIZMERIMYE szegmensek. Irracionális szám, PREDELY93
Az általános esetben a bizonyítás van kialakítva ugyanúgy, de nehéz bevezetni, hogy szükség van nehézkesebb jelöléssel. Tekintsük időszakos frakció a általános formája
p = 0, 1, 2 a a m 3 B 1 B 2 b 3. b n b 1 b 2 b n 3. b.
Jelöljük B = 0, b 1 b 2 b b n 3. periodikus része a bomlás. Akkor tudjuk írni
p = 0, 1, 2 a a m + 3. 10 -m B (1 + -n + 10 10 10 -2N + -3H +.).
Az expressziós zárójelben - a végtelen mértani, amelyre q = 10 -n. A összege a progresszió, képlet szerint (10) predy-
duschego pont megegyezik az 1 - 10 -n. és mivel
10 -m · B p = 0, 1, 2 + M-a 3. 1 - 10 -n.
Gyakorlatokat. 1) Spread tizedesekben következő racionális számok: 11 1. 13 1. 13 2. 13 3. 17 1. 17 2. bővítések és meghatározza időszakokban.
2) száma 142.857 az a tulajdonsága, hogy amikor megszorozva 2, 3, 4, 5 vagy 6, ott végre csak permutációját számok. Magyarázza az ingatlan épül a bomlási július 1 tizedes.
3) Lay megadott számok az 1. gyakorlatban végtelen frakciókat bázisokkal 5., 7. és 12.
4) Spread száma 1 3 egy biner frakcióval.
5) Írja meg bomlása 0,11212121. Állítsa milyen szám ez a 3 vagy 5 bázis.
5. általános meghatározása az irracionális számok az ajánlatkérő a szegmensben. . A 82. oldalon, az általunk bevezetett előzetes meghatározásához „szám” egy véges vagy végtelen tizedes. Egyetértettünk azzal a tizedessel, amelyek nem a racionális számok, irracionális számok hívni. Az eredmények alapján kapott az előző bekezdésben, ajánlhatunk szövege a következő: „a numerikus folytonosság, illetve a rendszer a valós számok (” valódi „számok szembe itt” képzeletbeli „vagy” komplex”, lásd 5. §), a gyűjtemény mindenféle végtelen tizedes. " (Hozzárendelésével nullák,
Matematikai számrendszer
Ez, mint már említettük, a végső tizedes write
formájában egy végtelen, vagy van más út: az utolsó számjegy egy frakció helyébe egy - az 1. és adjatok meg számtalan kilences. Így láttuk, például 0,999. = 1 - lásd a 3.) ..
Racionális számok periodikus frakció; irracionális számok nem periodikus frakció. De ez a meghatározás nem teljesen kielégítő: valójában fejezetben láttuk azt, hogy a tízes számrendszer szerint a dolgok természetéből semmi különös kiemelkedik a többi lehetséges; ugyanúgy egy fog működni, például a bináris rendszer. Emiatt nagyon kívánatos, hogy egy általánosabb meghatározásában a folytonosság, független a választás a 10 alap vagy bármely más. Talán a legegyszerűbb módszer bevezetésével egy ilyen általánosítás
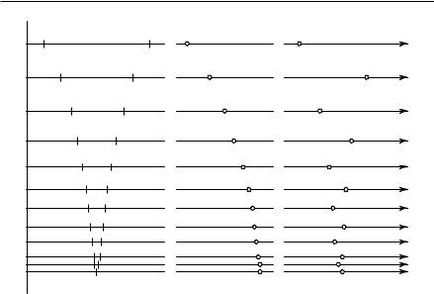
Tekintsük a valós tengelyt egy sorozata I 1. 2. 3. n. szegmenseket racionális végek; feltételezzük, hogy a következő szegmens tartalmazza az előző és az, hogy a hossza az n-edik intervallumot I n nullához N növelésével. Egy ilyen szekvenciát a „beágyazott” egymásba szegmens lesz az úgynevezett szerződő szegmensek sorozatában. Abban az esetben, decimális intervallumok hosszával megegyező I n 10 -n. de ugyanolyan sikerrel lehetne, mondjuk, 2 -n. vagy mi lehet korlátozni legalább
az a követelmény, hogy kevesebb, mint n 1. Most, hogy a következő
amelynek megfogalmazása kell tekinteni, mint az alapvető geometriai posztulátumot bármilyen szerződő szegmensek sorozatában, van egy és csak egy pont a valós tengelyének, amely szintén jelen van minden szegmensben. (Nyilvánvaló, hogy nincs több, mint egy ilyen pontot, mint a szegmensek hossza általában nulla, és a két különböző nézetek nem lehet egy intervallumban melynek hossza kisebb lenne, mint a pontok közötti távolság.) Ez a pont, definíció szerint, és ez az úgynevezett valós szám; ha ez nem racionális, ez az úgynevezett irracionális szám. Egy ilyen meghatározás, mi meg a levelezés pontok és számokat. Ez nem hozzá semmit igazán új: ahogy a meghatározása egy végtelen tizedes tört általánosabb formában hozomány.
Még ezen a ponton az olvasó kiterjedhet bizonyos kétségeket kell ismerni megalapozottnak. Hogy valójában mi az, hogy „pont” a valós tengelyen, ami azt feltételezzük tartalmazza egyidejűleg minden szegmensében szerződő szekvencia, ha nem felel meg a racionális szám? A válaszunk az, hogy létezik a valós tengelyen
§ 2NESOIZMERIMYE szegmensek. Irracionális szám, PREDELY95
Ábra. 11. összehúzható szegmensek. határait szekvenciák
(Figyelembe vett geometriai kép) szereplő fogalmakat minden szerződő szegmensek racionális végpontok, van egy alapvető geometriai posztulátum. Nincs szükség, hogy a csökkentés, így azt más matematikai állításokat. Vesszük elfogadottnak a matematika más axiómák vagy posztulátumok alapján intuitív hitelességét és hasznossága, talált, amikor az épület egy koherens rendszer matematikai állításokat. Formálisan tudtuk folytatni a számegyenesen, hogy úgy, hogy egy gyűjtemény néhány racionális pontokat csak, majd kell meghatározni azt a pontot az irracionális
szimbólum jelöli sorozata szerződő szegmensek. Irracionális pont teljesen szekvenciája határozza meg a racionális szerződő szegmensek, amelynek hossza általában nulla. Tehát mi az alapvető posztulátum ténylegesen képes kiszolgálni, mint egy definíció. Elfogadni egy ilyen meghatározás, miután csökkentették sorozata ajánlatkérő szegmensek intuitív értelemben, kijelentve: „létezését” irracionális pont - majd vidd a „mankó intuíció” által hivatkozott érvelésünk, és felismeri, hogy minden matematikai tulajdonságai irracionális pontot lehet érteni és szánták tulajdonságok szekvenciák szerződő szegmensek.
Egy tisztán matematikai szempontból ebben az esetben fontos az a tény, hogy a Belga meghatározása irracionális számok