Mi a kurtózis
kurtosis - negyedik pillanatban egy véletlenszerű változó eloszlása
az M (x-Mx) ^ 4? és hogy ilyen esetben is oznochaet kifejezést a „pozitív kurtosis”? totlko hogy nem nulla? negatív, mert nem lehet, ha jól értettem. Mi ennek a jelentése?
Ki a fene tudja.
Őszintén írta, amit az interneten talált a kifejezést még nem hallottam korábban.
Sokkal jobb, hogy kérje egy profi matematikus. Vagy azok, akik a tanulás a következő.
Jellemzően ezt arra használjuk, hogy meghatározzuk a normalitás a minta. Ha ez a kustorsis nagyobb, mint 0, akkor az eloszlási görbe ver-Tei (sűrűség) nagyobb, mint a normál görbe. Ha negatív, akkor már.
Vashche (látható képletű kstorsis - intézkedés az eltérés (szélesedés) egy központi pont.
Ez kustorsis nagyobb, mint 0, akkor az eloszlási görbe ver-Tei (sűrűség) nagyobb, mint a normál görbe. Ha negatív, akkor már.
vagy ez nem egy negyedik alkalommal, és a rossz (mint például néhány furcsa, mondjuk a harmadik, vagy nem tudom megérteni, hogy miért M (x-Mx) ^ 4 lehet negatív
> kustorsis
így kustorsis vagy kurtosis? vagy két különböző értékeket?
ps: szerinti Yandex, a szőnyeg függetlenül a várakozás és a szórásnégyzet, a kurtosis azonos három Gauss-féle eloszlás.
Itt senki nem hibázott! Hidd! Hazajövök, adok neked a pontos képletet. Akkor, azon az úton, kézi SPSS megnyitni.
Figyelj, én nem tudom, hogy jól spssam kézikönyveket, de a negyedik pont nem lehet negatív - ass esküszöm.
> Tud, mellesleg, kézi SPSS megnyitni.
ahol a következő lépés?
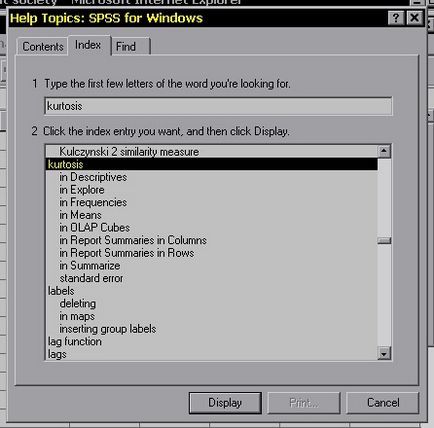
ps: szerinti Yandex, a szőnyeg függetlenül a várakozás és a szórásnégyzet, a kurtosis azonos három Gauss-féle eloszlás.
csak arra utal, hogy normál Gauss (amely ugyanaz, mint a normál) eloszlás. és általában minden mozzanatát a normál törvény függvénye matematikai várható értéke és szórása (mintha nem értette, miért tudom magyarázni, hogy a kurtózis nem lehet független
csak arra utal, hogy normál Gauss (amely ugyanaz, mint a normál) eloszlás.
Már tudtam
Általában minden mozzanatát a normál törvény függvénye matematikai várható értéke és szórása (mintha nem értette, miért tudom magyarázni, hogy a kurtózis nem lehet független
Jobb, hogy írjon, hogyan számolja meg. hogy mind a pillanatokban a Gauss-eloszlás függvénye az első három (akár nulla, azaz egy) azt mondta, egy évvel ezelőtt.
Kurtosis (variációs koefficiens vagy kurtosis) jelzi, hogy a szelíd forgalmazás (abban az esetben nagy értékek), vagy meredek. Kurtosis 0, ha a megfigyelések a szokványos törvény. CL-de ha a csúcsosság jelentősen eltér 0, a hipotézist a normalitás GS amelyből a mintát veszik, nem fogadható el!
E = (M (XM (x ^ 4 / D (X) ^ 4) -3. Így lehet mind pozitív, mind negatív. Bol a [-2,2]. Tud még egy másik szál, hogy levelet róla. És a aszimmetriát.
E = (M (X-M (x ^ 4 / D (X) ^ 4) -3
Most már értem, hogy miért a negatív. Indultam a meghatározása „a.
Tud még mindig az a húr, hogy írjon róla. És körülbelül aszimmetria.
Én nagyon hálás lesz.
Most várja meg, amíg az este. 20:00 után négy-menet zabatsayu. Csak olvasni a teljes listát a kérdést.
Nos, amíg a kérdés, mesélj aszimmetria.
Torzítottság (aszimmetria koefficiens r) - olyan intézkedés, az eltérés a gyakorisági eloszlás szimmetrikus eloszlását. Normális eloszlás az aszimmetria egyenlő 0. Ha igen, az aszimmetria pozitív, a csúcs az aszimmetrikus eloszlása balra mozog, és fordítva: ha az aszimmetria negatív, a csúcs - JOBB.
Ferdeség = (M (X-M (X ^ 3) / D (X) ^ 3
Negatív kurtosis jelezne vékony farkú adatok eloszlása, és azt mondják, hogy platykurtic. Pozitív kurtosis jelezne zsír farkú forgalmazás, és azt mondják, hogy leptokurtic. Normál eloszlás nulla kurtosis, és így a standard fecskefarok kialakítású. Azt mondják, hogy mesokurtic.
A kurtosis van -1,5116, ami azt jelzi, hogy az időtartam platykurtic. Ez összhangban van azzal a ténnyel, hogy a hisztogram nem harang alakú.