Ha görbe pályájú mozgás gyorsulás pont
Adjuk meg a sebességet a nyúlvány (1.1) az időpontban t1 = 2 c:
A sebessége 16,3 m / s.
Normál gyorsulás pontot. Ezután a görbületi sugara a pálya. Adjuk. Ábra. 1.1 kellene
ahol a - közötti szög teljes gyorsulás és a normál gyorsulás. By feltételezés - a nehézségi gyorsulás. Továbbá, az ábrán azt látjuk, hogy. Következésképpen, a görbületi sugár a pálya. Kiszámítható.
2. példa Egy anyagi pont mozog összhangban az egyenleteket:
X = A + Bt + Ct 3. y = kt + Lt 2 (1.2)
ahol A m = 3, B = 1 m / s, C = -1 m / s 3. K = 1,5 m / s, L = 2 m / s 2.
Keresse meg a koordinátákat, a sebesség és uskorenietochki t = 1 c.
Határozat. Koordináták tochkinaydem, helyettesítve az egyenletek a mozgás (1,2) numerikus értékek a együtthatók A, B, C, K, L ivremeni t:
A kiemelkedések a pillanatnyi sebessége a pontot az x-tengely, Y jelentése az első derivált a koordináta (1.2) in idő:
Ha T = 1 c; . Nagysága a sebesség m / s.
Mi található a vetítés gyorsulása, figyelembe első deriváltjának a sebessége a nyúlványok (1.3) időpontja:
A gyorsulás pontot.
A t = c 1 m / s 2 m / s 2 m / s 2.
3. példa A test körül forog egy rögzített tengely körül a törvény alatt
ahol A = 10 rad, B = 20 rad / s, G = -2 rad / s 2. megtalálni a sebesség és a gyorsulás a pont, megtalálása-scheysya távolság r = 0,1 m-re a forgástengely, t = 4 . Kijelző sebességvektorokkal és gyorsulás az ábrán.
Határozat. A sebesség pont a test, körül forgó rögzített tengely által meghatározott képlettel. ahol w - szögsebessége a test modul. A szögsebesség w találni azáltal, hogy az első derivált-nek az elfordulás szögét (1,5) alatt az idő:
A t = 4 c modul szögsebesség
Speed pont m / s.
Teljes gyorsítás pont mozog a görbe vonal, megtalálható például a geometriai összege a tangenciális gyorsulás. irányul érintőlegesen az utat, és a normál gyorsulás. felé és a görbületi középpontja a pálya (1.2 ábra.):
Mivel a vektorok egymásra merőleges, a gyorsulás modul. (1.7)
A modulok az érintőleges és normál gyorsulás pont a forgó test által adott:
ahol e - egy modul van szöggyorsulással.
Behelyettesítve expresszió és az AN a képlet (1,7), azt látjuk,
Szöggyorsulással találni azáltal, hogy az első derivált-nek a szögsebesség (1.6) időpontja:
Behelyettesítve a értékei W, E és R jelentése a (1.9), megkapjuk
Vector tangens ellen gyorsulási sebessége óta szöggyorsulással.
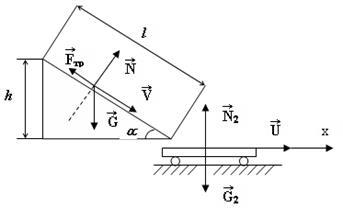
4. példa Box m1 = súlya 20 kg a tálcán lecsúszik hossza L = 2 m egy súrlódási együttható f = 0,1 a stacioner kocsi homokkal és ragadt ott. Kocsi homoktömegben m2 = 80 kg szabadon (súrlódás nélkül) schatsya kapcsolja-sínen a vízszintes irányban. Oprah szakadék sebességű u kocsi rekesszel, ha a tálca nen dőlésszög = 30 ° a sínek.
Határozat. A kosár és a doboz lehet tekinteni, mint egy olyan rendszer két kölcsönható testek rugalmatlan. De ez a rendszer nem zárt, hiszen van kitéve a külső erők: gravitációs G1 = m1 G és G2 = m2 g, és a reakció erő N2 (1.3 ábra.). Ezért alkalmazzák a törvény lendületmegmaradás általánosságban a rendszer „box - targonca” nem lehet. Azonban, mivel a kiemelkedés az említett erők irányában az x tengely egybeesik az irányt a sínek nullával egyenlő, akkor a nyúlvány a lendület ebben az irányban lehet kiindulni konstans, azaz
ahol P1X és P2X - box impulzus kiemelkedés és a kocsi a homokkal idején előfordulási a fiókot kocsi; p'1x és p'2x - ugyanazokat az értékeket, miután csepp mezőbe.
Figyelembe véve a rendszer a szervezet, mint az anyag pont, expresszálható egyenletben (1.10) impulzusokkal szervek révén tömege és sebessége, figyelembe véve, hogy R2X = 0 (kocsi az interakció-következmény egy rekesz a többi), és hogy miután a kölcsönhatás a két rendszer szervek együtt mozognak ugyanolyan sebességgel, és:
ahol v1 - sebesség modul doboz esett a kocsi; - a vetülete a sebesség az x tengelyen.
Tól (1.11). (1,12)
v1 sebesség egység kerül meghatározásra a törvény az energiamegmaradás egy dobozban mozgó tálcán alapján a súrlódási erő FTR:
Behelyettesítve v1 a képletben (1,12), megkapjuk
Kiszámítjuk a sebességet a kocsi:
5. példa Ferry tömege m1 és az L hosszúság van rögzítve a víz. Annak tat a tartály súlya m2. A tartályt ezután költözött az íj a komp saját csapból. A távolból s mozgatott gőz képest az alján? Force súrlódás és húzza előre elhanyagolt.
Határozat. gőz-konténer rendszer tekintetében a vízszintes irányban lehet tekinteni zárva. A törvény lendületmegmaradás, ebből következik, hogy a belső erők a zárt rendszer a testek nem tudja megváltoztatni a pozícióját a tömegközéppont. Ezért, ha mozog a tömeg közepén a tartály rendszert, azaz. C nem változtatta meg álláspontját aljához viszonyítva. Koordinátája a tömegközéppontja rendszer által adott XC, ahol m - tömeg a rendszer; km - tömege szervek.
Mi választjuk ki a koordináta-rendszert úgy, hogy a Oy tengely tartott a kezdeti időpontban a C1 - központ tömeg komp. Jelöljük a tömegközéppontja koordináták x1 komp T C1 és X2 -. R a tömegközéppontja a tartály C2 -. Mielőtt mozgása (1.4 ábra.), X'1. X'2 - a mozgás után.
A központ a tömeg a rendszer nem változott, így
Az ábrából következik, hogy. - mielőtt elmozdulás. - az áthelyezés után. Mi beszerezni (1.14):
6. példa tavaszán a tüzelési fegyvert függőlegesen golyó tömege m = 20 g magasságig H = 5 m. Annak meghatározására, a merevsége k a rugó pisztoly, ha nyomóerővel x = 10 cm. Mass tavaszi és súrlódási erők elhanyagolt.
Határozat. Képzeljünk el egy rugó rendszer - egy golyó. Mivel a rendszer a szervezet csak konzervatív erők, akkor a probléma megoldására, akkor lehet alkalmazni, az energia-megmaradási törvény a mechanika. Elmondása szerint, a teljes mechanikai energia E1 a rendszer a kezdeti állapotban (ebben az esetben, mielőtt a lövés) egy teljes Ener GIES E2 a végső állapotban (amikor a golyó magasságig H), t. E.
ahol T1. T2. P1 és P2 - kinetikus és potenciális energia a rendszer a kezdeti és a végső állapot. Mivel a kinetikus energia a lövedék a kezdeti és a végső államok-nulla, akkor az egyenlet (1.15) a forma-met
Tegyük fel, a potenciális energia a golyó a térerősség tyago Taenia földön, amikor a golyó nyugszik egy nyomórugót, egyenlő nullával, és az emelési magasság a golyó kell mérni végétől az összenyomott rugó. Ezután a rendszer energiája az eredeti állapothoz, hogy egyenlő a potenciális energia az összenyomott rugó, azaz . és a hosszú távú álló SRI - potenciális energiája a lövedék a magassága h. azaz .
Behelyettesítve expressziós P1 és P2 a (2) képlet, Nai DEM. hol. (1,17) Tegyük ellenőrzi, hogy az így kapott általános képletű ad egy egység merevségét k. Erre a célra a jobb oldali (1,17), hanem a mennyiségek helyettesítheti a egységek:
Miután meggyőződtünk, hogy a kapott egység EDI nitsey-keménység (1 N / m), behelyettesítve (3) képietű ZNA-cheniya mennyiségeket és számításokat végeznek:
7. példa Ball tömeg m1. Horizon-tal mozog egy bizonyos sebességgel V1, összeütközött egy álló labdát tömege m2. Tökéletesen rugalmas golyót, megüt egy egyenes, központi. Mi frakció k a mozgási energiát a második adta az első labdát?
Határozat. Az energia aránya által továbbított első labdát a második által kifejezett kapcsolatban
ahol - a kinetikus energia és a sebesség az első labdát a csap; U2 és T2 - sebesség és kinetikus energiája a második labdát az ütközés után.
Amint látható az (1.18) meghatározására k kell találni. A feltétel szerint a probléma, a pulzáló rendszer két golyó képest vízszintes irányban nem változik, és a mechanikai energia a golyó a másik nem adja át. Ezzel, azt találjuk:
Együtt fogjuk megoldani egyenlet (1.19) és (1.20):
Behelyettesítve u2 (1,21) a (1,18) és csökkent a v1 és M1. megkapjuk
A talált összefüggést, hogy a továbbított aránya távú energia függ csak a tömeget az ütköző golyó.