Az átviteli függvény Online
Meghatározásával az átviteli függvény (PF) egy olyan üzemben, amely az aránya a képek és a kimeneti koordináta input zéró kezdeti feltételek:
Kinevezés szolgáltatás. A vezérlő objektum (Op) által leírt lineáris differenciálegyenlet n sorrendben. A vibrációs szintet n-edik érdekében meghatározzuk:- átviteli függvény;
- frekvencia jellemzők (amplitúdó (AFC), a fázis (FRF), a tolattyú (LCHH));
- és tranziens impulzusválasz (tömeg) függvény;
- tranziens grafikonok és frekvenciája.
Ahhoz, hogy megtalálja az átviteli függvény kell választani interneten
Példa. A vezérlő objektum (Op) által leírt lineáris differenciálegyenlet a harmadik sorrendben:
(2)
1) átviteli függvénye az OS általában képviseli a kapcsolat
W (i # 969;) = a (# 969;) E i # 966; (# 969;) = U (# 969;) + IV (# 969;)
ahol R (p) és Q (p) - Laplace képkimenet OU és a bemeneti változók megfelelő bal és jobb oldalán az 1. egyenletben Ennélfogva, az átviteli függvény lesz a formában:
(3)
vagy
. (4)
2) határozza meg a frekvencia karakterisztika a op-erősítő. Ismeretes, hogy a frekvencia átviteli függvény W (# 969;) lehet ábrázolni, mint:
, (5)
ahol A (# 969) - egy amplitúdó frekvencia jellemzői (AFC);
# 966, (# 969) - a fázis frekvencia jelleggörbét (PFC);
U (# 969) - a tényleges frekvencia (VCHH);
V (# 969) - a képzeletbeli frekvencia jellemző;
Helyettesítse az i # 969; A (3) kifejezés helyett p. kapjuk:
(6)
Alapján a kifejezéseket (5) és (6), hogy külön amplitúdó és fázis frekvencia karakterisztika és a helyettesítő számszerű értékeket a együtthatók. Azon a tényen alapul, hogy:
Egy (# 969;) = | W (i # 969;) |
# 966, (# 969;) = arg (W (i # 969;))
(Lásd. A komplex számok). Végül kapjuk: (7)
3) Adjuk meg a logaritmikus amplitúdójú frekvencia jellemzői (LACHH).
Ismeretes, hogy a LACHH meghatározható a kapcsolatot:
L (# 969;) = 20lg (A (# 969;)) (8)
Ez a jellemző a dimenzió dB (decibel), és megmutatja a változás aránya kimeneti értéket a bemeneti teljesítmény. Kényelmi LACHH építeni egy logaritmikus skálán.
A fázis frekvenciamenet, épült egy logaritmikus skála, a logaritmikus fázis lesz az úgynevezett frekvencia válasz (LFCHH).
Példák az építési és LACHH LFCHH a mi kezdeti adatok az 1. ábrán látható.
Mi határozza meg az impulzus válasz (tömeg) funkciót. A súly függvény w (t) az a rendszer válasz az egység impulzus funkció, benyújtva a bemenetére. A súlyfüggvény kapcsolódik az átviteli függvény Laplace transzformáció.
. (9)
Ezért a súlyozó függvény megtalálható alkalmazásával inverz Laplace transzformáció az átviteli függvényeket.
w (t) = L -1 [W (p)] (10)
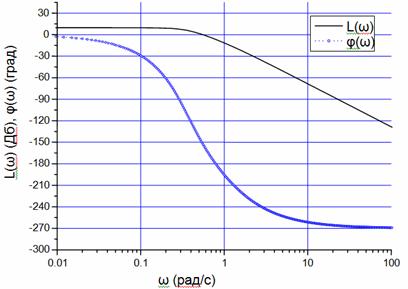
1. ábra - L (# 969) - LACHH rendszer (Db); # 966, (# 969) - LFCHH rendszer (fok); # 969; - a bemeneti jel frekvenciáját (rad / s)
Kiszámítjuk megközelítőleg a gyökerek a polinomok R (p) és Q (p). majd megtalálni az inverz Laplace transzformáció az átviteli függvény és cselekmény súlyozó függvény (2. ábra). A súlyfüggvény származik az átviteli függvény H (t). amely egy rendszer lépésről választ. Integrálása w (t), vagy a teljesítő inverz Laplace transzformáltja W (p) / p. Azt találjuk, a válasz függvény h (t), és össze egy megfelelő grafikon (3. ábra).
,
.
2. ábra - Az időbeli jellemzőit. A impulzusválasz-függvény w (t)
3. ábra - Az átmenet függvény h (t)