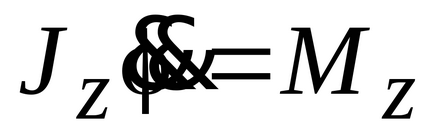Általánosított erők és számítási módszereket
Tekintsünk egy mechanikus rendszer ideális korlátok. Hagyja aktív villamosenergia-rendszer. Adjunk egy mechanikus rendszer virtuális elmozdulás és kiszámítja az elemi rendszer működését erők ebben a mozgás:
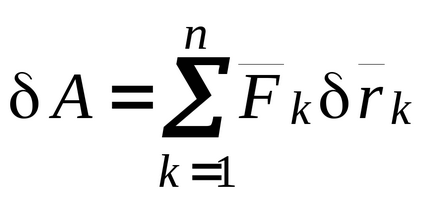
Használata (17.2) expresszálják a variációs
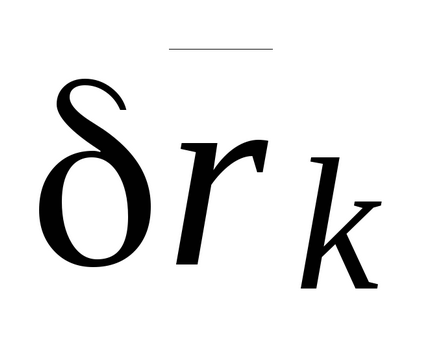
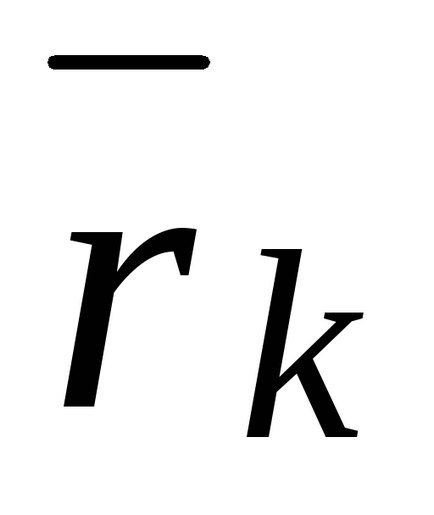
Csomópont (17,6) a sorrendben összegzése:
Jelöljük a kifejezést (17,7)
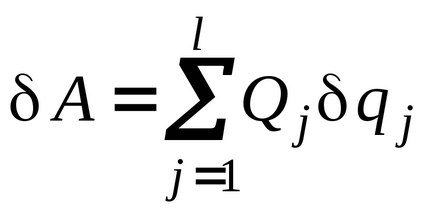
SilamiQjnazyvayut általánosított variációs koefficiens az általánosított koordináták szempontjából az elemi erők a rendszer.
Attól függően, hogy a méret variáció és az általános koordináták
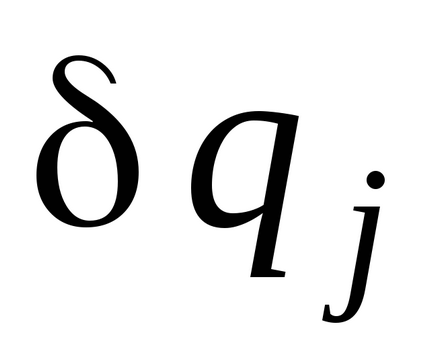
Kiszámításához használt módszerek általános erők
Nézzük meg a három módon lehet kiszámítani az általánosított erők.
1. A primer generalizált erők képletű (17,8)
Képlet (17,9) a gyakorlatban ritkán használják. Problémák megoldásában, gyakrabban használják a második módszer.
2. A módszer a „befagyasztása” általánosított koordinátákat.
Adunk egy mechanikus rendszer egy virtuális mozgalom, amelyben az összes variáció az általánosított koordináták kivéve
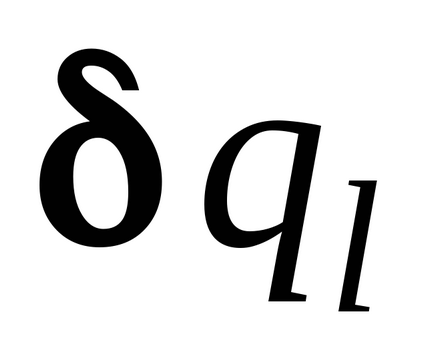
.
Számoljuk ezt mozgó munka
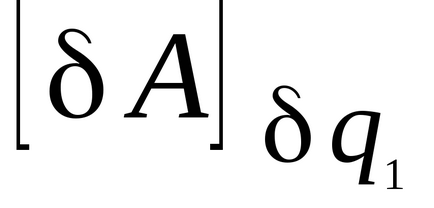
.
A meghatározás szerint a variációs koefficiens
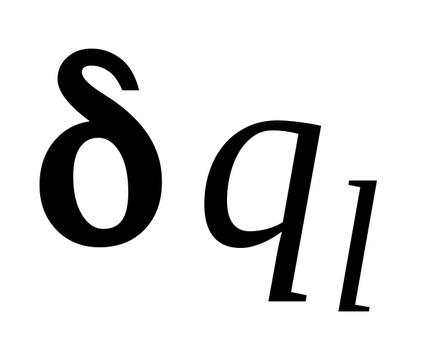
Ezután, hogy a rendszer egy virtuális elmozdulás
és határozza meg a második általánosított erő Q2. kiszámításakor a virtuális munka rendszer összes erők
.
Hasonlóképpen, kiszámítja az összes többi általános erők a rendszer.
3. Az esetben, ha a potenciális erőtér.
Tegyük fel, hogy ismert potenciális energiáját mechanikai rendszer
.
Ezután a képlet (32,8)
A virtuális munka elve a statikai általános koordinátákkal
Elve szerint a virtuális elmozdulások a statikus egyensúly tökéletes utasbiztonsági holonomic, álló korlátok szükséges és elégséges feltétel
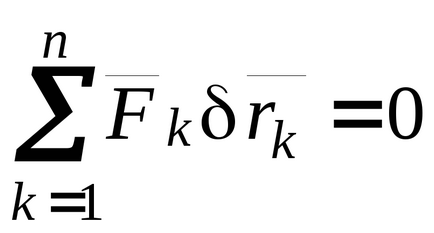
Rátérve az általánosított koordinátákat,
Mivel a változás a generalizált koordináták függetlenek, akkor a eltűnő a kifejezés (17.11) csak akkor lehetséges, ha az összes variációs koefficiensek az általánosított koordinátákat nullával egyenlő:
Így, hogy egy mechanikus rendszer ideális, holonomic, helyhez kötött és a gazdaság kapcsolat egyensúlyi akkor és csak akkor, ha az összes általános rendszer erők nulla (nulla kezdeti rendszer sebességét).
Lagrange egyenlet generalizált koordináták (másodrendű Lagrange egyenlet)
Lagrange egyenleteket származnak az általános egyenlet a dinamika a cseréje virtuális elmozdulásainak azok kifejeződése szempontjából a variáció a generalizált koordinátákat. Ezek egy differenciálegyenlet-rendszert a mozgás mechanikai rendszer generalizált koordinátákat:
ahol
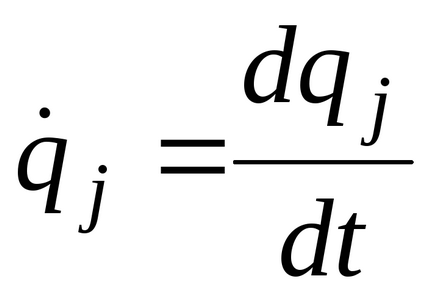
T kinetikus energia a rendszer, képviselt függvényében az általánosított koordináták és generalizált sebességek
,
A számú egyenlet (17.13) határozza meg a számát szabadsági fok és nem függ a szervek számát a rendszerben. Ideális kapcsolat a jobb oldali részei egyenletek szerint csak az aktív erők. Ha a kommunikáció nem ideális, a reakciójuk kell tulajdonítani az aktív erők.
Abban az esetben lehetséges ható mechanikai egyenletrendszer (17.13) formájában
.
Ha bevezetjük a Lagrange L = T P. kap, hogy a potenciális energia független a generalizált sebességek, megkapjuk a Lagrange egyenleteket a második fajta esetében a potenciális erőket az alábbi űrlapot
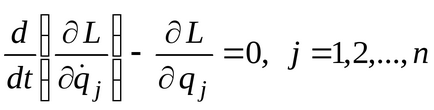
Összeállításakor a Lagrange egyenleteket a második fajta kell végre a következő lépéseket:
Állítsa be a számát szabadsági fokú mechanikai rendszer, és válaszd a generalizált koordinátákat.
Hozzon létre egy kifejezés a kinetikus energia a rendszer, és azt bemutatja függvényében az általános koordináták és sebességek általánosított.
A fentiekben leírt módszerekkel, hogy megtalálják a generalizált rendszer az aktív erők.
Felelnek meg a szükséges egyenletek Lagrange differenciálás.
Mi alkotják a differenciálegyenlet a forgómozgásának egy merev test hatása alatt egy olyan rendszer aktív erők (ris.17.3) a fenti algoritmus.
1. A testület végzi forgó mozgás, amelynek egy szabadságfoka van. Az általános koordináta fogadja szög :
2. A mozgási energia egy test körüli forgás rögzített tengely
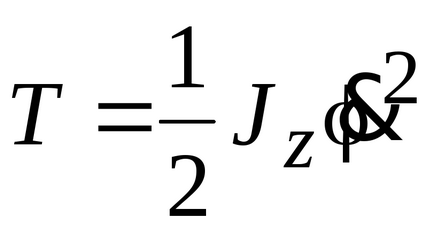
Jz test, ahol a tehetetlenségi nyomatéka forgástengelye körüli z.
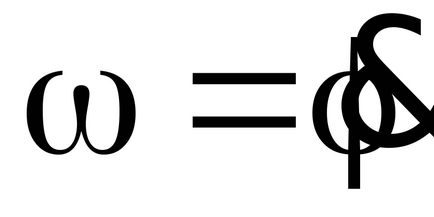
3. Határozza meg az általánosított erő. Ad a test egy virtuális mozgó és kiszámítja a virtuális munka az összes aktív erők a rendszer:
.
Ezért, Q = Mz fő pillanata erők viszonyítva az aktív rendszer test forgástengelyével.
4. Végezze el a műveletet a differenciálás a Lagrange-egyenlet
Behelyettesítve egyenlet (17.15) egyenletben (173
14) megkapjuk a differenciálegyenlet a forgómozgásának a test