Quadrature demodulátor, iLab
Shenyagin AS BTSm-111
A jelenlegi szakaszban a technológiai fejlődés, sokkal könnyebb és biztonságosabb vevők digitális jelfeldolgozás. Digitalizálása az RF jel közvetlenül korlátozódna, mivel a modern digitális áramkörök gyakran nem optimális, kielégíti a tétel feltételei Kotel'nikova-Shannon. Fent azt mondták, hogy a komplex burkoló tartalmazza az összes szükséges információt, hogy dekódolja a jeleket, és kiszámítjuk a számosságát és fázis jellemzői. Komplex burkoló Keskeny sávú jelek jelentése egy pár alacsony frekvenciájú jelek alkalmas digitalizálására (feltételek törés nélkül Kotel'nikova tétel).
A vydelenieya komplex burkoló jel heterodyning' alkalmazott eljárás. Ennek lényege a következő. RF bemeneti jel s (t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) megszorozzuk az oszcilláció a két oszcillátor (LO) gyakorisággal ω0, eltolt fázisban egymáshoz képest szögben π / 2 - cos (ω0 ∙ t) és -sin (ω0 ∙ t).
s (t) ∙ cos (ω0 ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ω0 ∙ t) =
0,5 ∙ A (t) ∙ cos (φ (t)) + 0,5 ∙ A (t) ∙ cos (2ω0 ∙ t + φ (t)) =
s (t) ∙ (-sin (ω0 ∙ t)) = - A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ sin (ω0 ∙ t) =
0,5 ∙ A (t) ∙ sin (φ (t)) - 0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)) =
0,5 ∙ q (t) - 0,5 ∙ A (t) ∙ sin (2ω0 ∙ t + φ (t)) (2)
A képletek (1) és (2), amelyek tartalmazzák az eredmények szorzataiból két komponens - egy kisfrekvenciás 0,5 ∙ i (t) és 0,5 ∙ q (t), amelyek a valós és képzetes része a komplex burkoló a magas frekvencia és 0,5 ∙ a (t) ∙ cos (2ω0 ∙ t + φ (t)), és -0,5 ∙ a (t) ∙ sin (2ω0 ∙ t + φ (t)), amelyet el lehet távolítani a aluláteresztő szűrő (LPF) . Ábra 1-2 mutatnak kvadratúra áramkört (vektor) demodulátor egy fázistoló vagy anélkül fázistoló.
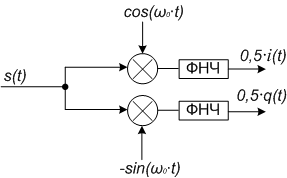
1. ábra - A működési diagramja a vektor demodulátor
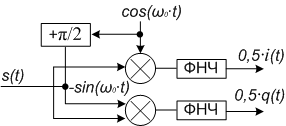
Ábra 2-működőképes vektor diagram fázis demodulátor
Vektor demodulátor által leírt képletek (1) és (2), hogy kap egy „szép” nézetben csak akkor, ha a helyi oszcillátor referencia jel azonos frekvencia és kezdeti szakaszában egy referencia oszcillációs ω0 (azaz, vivőhullám jel és a helyi oszcillátor koherens vevő). Ez az állapot lehet elérni szervo rendszerek, amelyek alapján a fáziszárt hurok áramkör (PLL, PLL). Ha ez nem áll rendelkezésre, a kimenet a kvadratúra- demodulátor megkapjuk két összetevője az úgynevezett veri gyakorisága függ a hiba gyakorisága heterodin vevő és a vivőfrekvencia a vett jel. Mismatch a kezdeti szakaszban a heterodin vevő és a vivőfrekvencia a vett jel torzítás szintjét kvadratúra előrejelzések. Ebben az esetben azt mondjuk, hogy a komplex burkoló vett jel a frekvencia ωg.
Bemutatjuk matematikailag a helyzetet. Legyen a frekvencia a vevő helyi oszcillátor ωg = ω0 + δω, a kezdeti szakaszban - φg. majd:
s (t) ∙ cos (ωg ∙ t) = A (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ cos (ωg ∙ t + φg) =
A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ cos (ω0 ∙ t + φ (t) - ωg ∙ t -φg) = ...
Csoport A koszinusz feltételeit kiemelve külön nevezni φ (t), és felbontható képletekkel hozzáadásával érvek:
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) + ...
+A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) = ...
Mivel ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ cos (δω ∙ t + φg) + ...
+ A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ sin (δω ∙ t + φg) = ...
= 0,5 ∙ i (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
-0,5 ∙ q (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) + ...
+0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + ...
+0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
Miután LPF van
Ib (t) = 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
s (t) ∙ sin (ωg ∙ t) = (t) ∙ cos (ω0 ∙ t + φ (t)) ∙ sin (ωg ∙ t + φg) =.
A (t) ∙ 0,5 ∙ sin (ω0 ∙ t + φ (t) + ωg ∙ t + φg) + A (t) ∙ 0,5 ∙ sin (ωg ∙ t + φg - ω0 ∙ t -φ ( t)) =.
Csoport A koszinusz feltételeit kiemelve külön nevezni φ (t), és felbontható képletekkel hozzáadásával érvek:
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ω0 + ωg) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((ωg - ω0) ∙ t + φg) - ...
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((ωg - ω0) ∙ t + φg) = ...
Mivel ωg = ω0 + δω
= A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ A (t) ∙ 0,5 ∙ cos (φ (t)) ∙ sin (δω ∙ t + φg) -.
- A (t) ∙ 0,5 ∙ sin (φ (t)) ∙ cos (δω ∙ t + φg) =.
= 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) +.
+0,5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) +.
+ 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) -.
- 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
= - 0,5 ∙ q (t) ∙ cos ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ sin ((2 ∙ ω0 + δω) ∙ t + φg) -.
- 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) +.
+ 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg)
Miután LPF van
Qb (t) = 0,5 ∙ q (t) ∙ cos (δω ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δω ∙ t + φg)
Így, a kimenet a kvadratúra- demodulátor jel van két
Ib (t) = 0,5 ∙ i (t) ∙ cos (δω ∙ t + φg) + 0,5 ∙ q (t) ∙ sin (δω ∙ t + φg) (3)
Qb (t) = 0,5 ∙ q (t) ∙ cos (δω ∙ t + φg) - 0,5 ∙ i (t) ∙ sin (δω ∙ t + φg) (4)