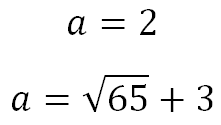A probléma a paraméter a kerülete
Helló kedves olvasók! Ma rábukkantam egy gyönyörű probléma paraméterrel, és szeretném megosztani veletek a döntést.
A kihívás ez: hogy megtalálják a pozitív paraméter értékét egy, oly módon, hogy a rendszer egy egyedülálló megoldás.
Azonnal látni fogja, hogy mindkét egyenlet - egy kör egyenlete. Az első sugara egyenlő három, a második - a. Érdekes, hogy a jelen első kör egyenlete x modul. Azaz, akkor valójában nem egy, hanem két kör szimmetrikus az y tengely és amelynek van egy központi ponton (5, 4) és (-5, 4), és a sugara a három. Ez egy kis trükk, hogy ezt a problémát, mert őszintén szólva, a cél nagyon egyszerű. Bal kitalálni, hogy a második kör sugarát a központ (-2, 0) lehet egy érintkezési pontja mindkét körök, csak ezen a ponton kell az egyetlen feladata az állapot. Nézd meg a képet:
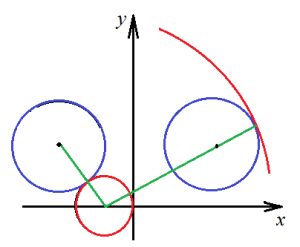
Látjuk, hogy a két megoldás van: vagy egy piros kör érintője a bal kék „belülről”, vagy egy piros kör sugara nyomja meg a helyes kék „kívül”. Minden más érintkezési pont nem az egyetlen: más esetekben egy piros kör feltétlenül érinti, vagy keresztezi mind a kék kört, és ez nem feltétele a problémát.
Keresse a sugara a piros kör, ez segít nekünk Pitagorasz-tétel (zöld háromszög). Ezután a közti távolságot a kis piros kör, és a kék (balra):
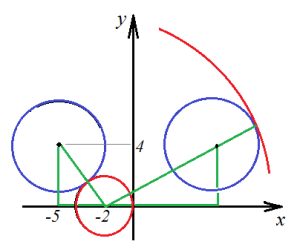
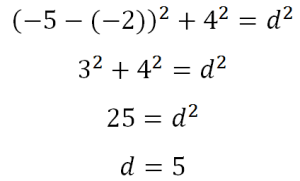
Ahhoz, hogy megtalálja a kívánt tartományban, meg kell kivonni ebből a távolságból 3:
Tekintsük most a második háromszög, és meghatározza a távolságot a központok nagy piros kör, és a kék (jobbra):
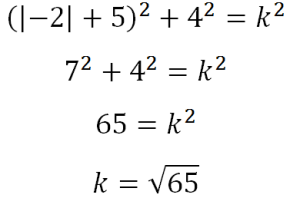
Ne felejtsük el, hogy ez a távolság szükséges hozzá egy sor kék kör: