Hogyan lehet megtalálni a magassága a trapéz
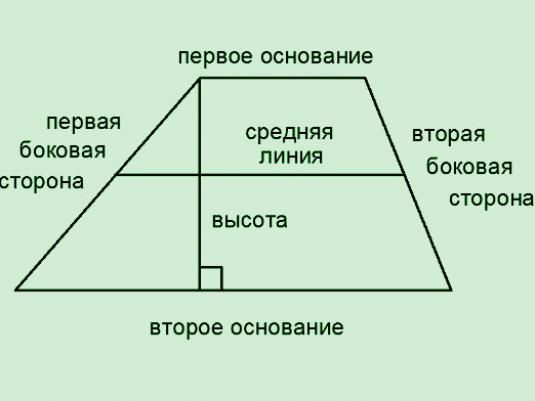
Trapéz úgynevezett egy téglalap két oldala, amelyek a párhuzamos (ez az alapja a trapéz ábrán feltüntetett A és B), amely a másik két - nem (a képen az AD és a CB). A magasság a trapéz - egy szegmens h tartott merőleges a bázisok.
Hogyan lehet megtalálni a magassága a trapéz egy ismert értékű területet a trapéz és a hossza a bázis?
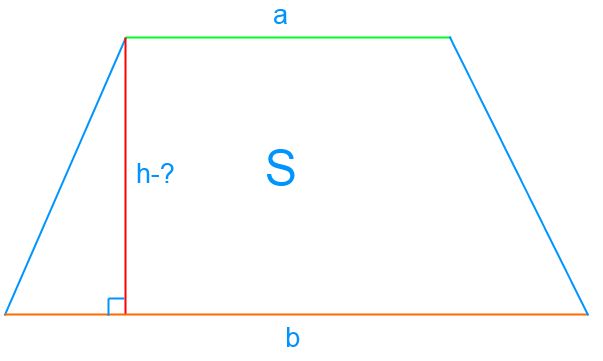
Területének kiszámítása S trapéz ABCD, használja a következő képletet:
Itt a szegmensek a és b - az alapja a trapéz, h - a magassága a trapéz.
Átalakítja a képlet, írhatunk:
Ezen képlet, megkapjuk az értéket H, ha az ismert értéke az S felület bázis és az értékeket a hosszak a és b.
Ha ismert, hogy a terület a trapéz S smsup2- 50, egy alap hossza 4 cm, és egy bázis hosszúságú b értéke 6 cm, hogy megtalálják a h magasság, a következő képlet segítségével:
Behelyettesítve az ismert értékeket a formula.
h = (2-50) / (4 + 6) = 100/10 = 10 cm
Válasz: A magasság a trapéz 10 cm.
Hogyan lehet megtalálni a magassága a trapéz, ha az adott érték a területet a trapéz és a hossza a középső sorban?
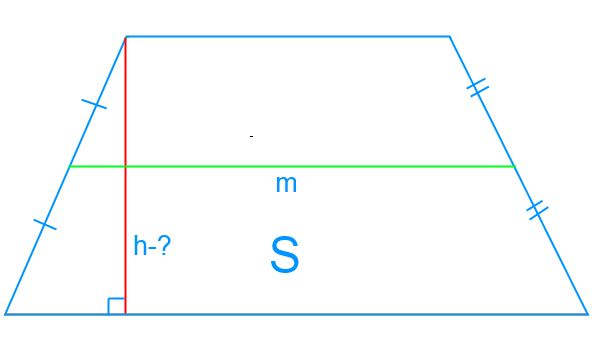
Használata formula számításának területe trapéz:
Itt m - Közel vonal, h - a magassága a trapéz.
Ha az a kérdés, hogyan lehet megtalálni a magassága a trapéz formula:
h = S / m, a válasz lesz.
Így találunk a értéke a trapéz h magasság, amelynek ismert értéke a szegmens területe S és a középső vonal m.
Ismert hossza a középvonal trapéz m, ami 20 cm-es, és az a terület S, ami megegyezik a 200 smsup2-. Keressük az érték a magassága a trapéz h.
Behelyettesítve az értékeket S és m, kapjuk:
h = 200/20 = 10 cm
Válasz: A magasság a trapéz 10 cm
Hogyan lehet megtalálni a magassága a téglalap trapéz?
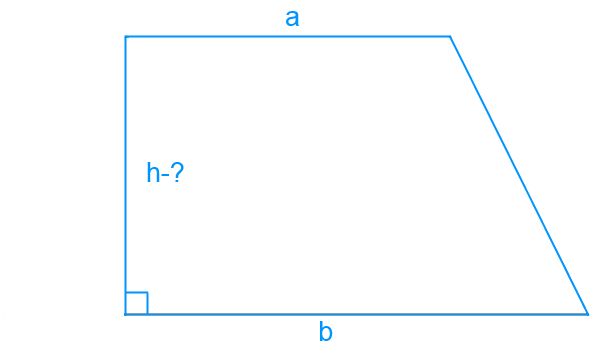
Ha a trapéz - egy négyszög két párhuzamos oldala (bázisok) a trapéz. Ezután az átlós - egy szegmens, amely összeköti a két szemközti sarkait a tetején a trapéz (AC szegmens az ábrán). Ha egy derékszögű trapéz keresztül átlósan találni trapéz magasságot h.
Négyszögletes trapéz hívják ezt trapéz, ahol az egyik oldalán függőleges is az alaplapra. Ebben az esetben, a hossza (AD) azonos h magassága.
Szóval, úgy egy téglalap alakú trapéz ABCD, ahol AD - a magasság, DC - az alapja, AC - az átlós. Mi használjuk a Pitagorasz-tétel. AC négyzete átfogó egy derékszögű háromszög ADC egyenlő a négyzetének összege a lábak AB és BC.
Akkor tudjuk írni:
ACsup2- = ADsup2- + DCsup2-.
AD - ez a láb a háromszög oldalai a trapéz, és ugyanabban az időben, a magassága. Miután a szegmens AD merőleges a bázisok. A hossza a következő lesz:
AD = radic- (ACsup2- - DCsup2-)
Tehát, mi van a képletet a magassága a trapéz h = AD
Ha a hossza a négyszögletes alapja a trapéz (DC) egyenlő 14 cm, és az átlós (AC) 15 cm, a magassága értéket (AD -bokovoy oldalán) használja a Pitagorasz tétel.
Legyen x - egy ismeretlen egy derékszögű háromszög (AD), majd
ACsup2- = ADsup2- + DCsup2- felírható
15sup2- = 14sup2- + hsup2-,
X = radic- (15sup2--14sup2-) = radic- (225-196) = Radic-29 cm
Válasz: A magasság a téglalap alakú trapéz (AB) lesz Radic-29 cm, ami megközelítőleg, 5,385 cm
Hogyan lehet megtalálni a magassága a egyenlő szárú trapéz?
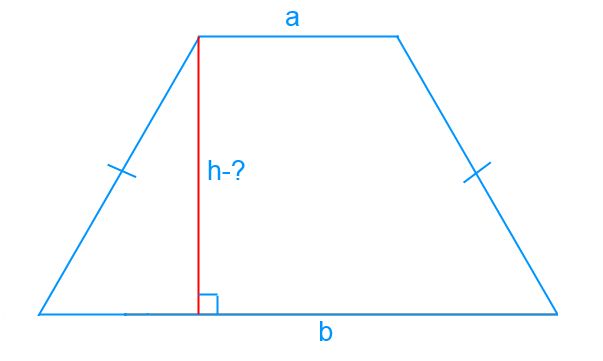
Egyenlő szárú trapéz úgynevezett trapéz, amelyek oldal egyenlő hosszúságú. Az egyenes vonal át húzott a közepén egy trapéz bázis a szimmetriatengely. Egy különleges eset egy trapéz, amelynek átlói merőlegesek egymásra, akkor a magasság h h, és az egyenlő lesz a fele az összeget a bázisok.
Vegyük azt az esetet, ha az átlók nem merőlegesek egymásra. A egyenlőszárú (egyenlő szárú) trapéz egyenlő szögek a bázisok és a hossza a átlók egyenlő. Az is ismert, hogy az összes csúcsainak egy egyenlő oldalú trapéz kapcsolódnak kerületi húzott vonal körül ez trapéz.
Tekintsük rajz. ABCD- egyenlő szárú trapéz. Ismeretes, hogy alapja a trapéz párhuzamos eszközökkel, BC = b párhuzamos AD = egy, oldalsó AB = CD = c, akkor, a sarkokat a bázisok illetve felírható szög BAQ = CDS = alfa-, és az ABC szög = BCD = béta. Arra következtettünk, egyenlőségét a háromszög ABQ háromszög SCD, majd vágjuk
AQ = SD = (AD - BC) / 2 = (a - b) / 2.
Azzal a feltétellel, a problémát, és egy bázis értéket b, és az oldalsó hossza s, azt találjuk, trapéz h magasság, egyenlő a szegmens BQ.
Vegyünk egy derékszögű háromszög ABQ. IN - a magassága a trapéz merőleges az alapja az AD, így a szegmens AQ. AQ oldalán a háromszög ABQ találunk, a származtatott korábbi képlet szerint:
Az értékek a két lába egy derékszögű háromszög, az átfogó találni BQ = h. Használja a Pitagorasz-tétel.
ABsup2- = AQsup2- + BQ²
Mi helyettesítheti ezeket a feladatokat:
csup2- = AQsup2- + hsup2-.
Kiszámoljuk a magasságban egyenlő szárú trapéz:
Dana egyenlő szárú trapéz ABCD, ahol a bázis AD = a = 10 cm, a BC alap = b = 4 cm, és oldalsó AB = c = 12cm. Ilyen körülmények között, ha egy olyan példát, hogyan kell megtalálni a magassága a trapéz, egyenlő szárú trapéz AVSD.
Keressük az oldalsó AQ háromszög ABQ, hogy ebben az esetben az ismert adatok:
AQ = (a - b) / 2 = (10-4) / 2 = 3 cm.
Most helyettesítheti az értékeket egy háromszög oldalai a képlet a Pitagorasz-tétel.
h = radic- (csup2-- AQsup2-) = radic- (12sup2-- 3sup2-) = Radic-135 = 11.6sm.
Válasz. A h magassága egy egyenlő szárú trapéz ABCD 11,6 cm.