Maximális áramlási probléma - studopediya
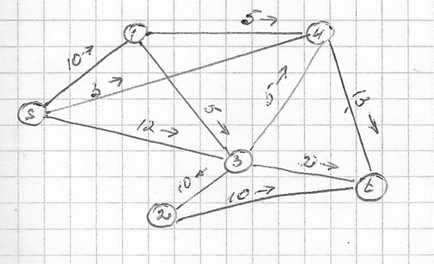
Tekintsük meghatározásának problémáját a maximális áramlási között a csatlakoztatott dedikált hálózati csomópontok. Minden ív a hálózat kapacitása mindkét irányban, amelyek meghatározzák a maximális átfolyó áram egy adott íven. Orientált (egyoldalas) az ív megfelel a nulla kapacitását a rossz irányba.
Hálózati kapacitás Cij is képviselteti mátrix formában.
1. lépés:
Találja el a célt, amely összeköti a forrás S és lecsepegtetjük t. ahol az áramlás veszi pozitív értéket. Az irány S → t. Ha egy ilyen cél nem létezik, folytassa a 3. lépéssel Ellenkező esetben folytassa a 2. lépéssel.
Legyen () - sávszélesség ívek lánc (S, T) irányába S → T (t → S).
Mátrix teljesítmények C = [Cij] a következőképpen változik:
a) levonja # 1012; minden;
b) hozzá # 1012; minden.
Cserélje a jelenlegi C mátrix az újonnan megszerzett, és lépjen a 1. Művelet (a) lehetővé teszi, hogy használja maradékok áteresztőképesség lánc kiválasztott ívek irányába S → t.
Operation (b) visszaállítja az eredeti hálózati kapacitás miatt csökkenése áteresztőképesség az ív ugyanabban az irányban lehet tekinteni, mint a növekedés annak kapacitását az ellenkező irányba.
Keresse meg a maximális áramlás a hálózatban.
Legyen C = [Cij] - a kezdeti mátrix sávszélességet.
C * = [C * ij] - végső előállított mátrix módosításával a kezdeti mátrix (1. és 2. lépés).
Optimális áramlási X = [xij] az ívek meghatározása a következő:
A maximális fluxusát S t egyenlő:
Példa: Annak meghatározására, a maximális áramlás az oszlop
Ennek kiindulási áramkört válasszon S → 1 → 4 → t. Ezután a sejteket (S, 1), (1,4), (4, t) jelöli (-), és a sejteket (1, S), (4,1), (t, 4) vannak jelölve (+).
A maximális térfogatáram ez az áramkör
Lehetőség van kiválasztani egy másik áramkörben. Egy jó választás az, hogy a legnagyobb értéket # 1012;. De lehet, hogy sok változata van ilyen lánc. Amikor programozó áramkört, amely közvetlenül határozzuk meg a C mátrix, kezdve az első sorban a S-karakterlánc, és kiválasztja a következő csomópont közül azok, amelyek össze vannak kötve az S pozitív áramlást. Következő tartják a sorban megfelel a kiválasztott csomóponthoz, és kiválasztja a következő csomópontot csatlakozik az előző pozitív ív. A folyamat addig folytatódik, amíg majd. t, amíg egy csomópont eléréséig.
Mi állítsa be a C mátrix, kivonva # 1012; = 5 minden példány jelölt (-), és hozzáadjuk az összes elemet, amely a plusz (+). Kapunk egy új mátrixot.
Hasonló intézkedéseket tett, és az azt követő lépések elvégzésével.

Mi válasszuk áramkör (S → 3 → 2 → t)
# 1012; = min = 10 Helyes C mátrix
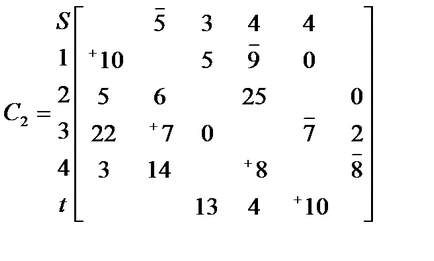
Mi válasszuk áramkör (S → 3 → 1 → 4 → t)
# 1012; = min = 5 Helyes C mátrix
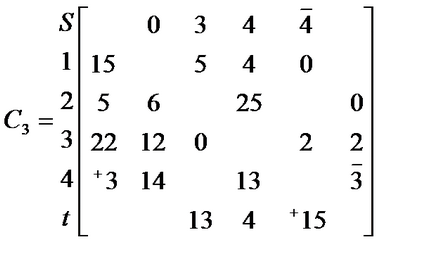
Mi válasszuk áramkör (S → 4 → t)
# 1012; = min = 3 Pontos C mátrix

Kiválasztjuk áramkör (S → 3 → t)
# 1012; = min = 2 Helyes C mátrix
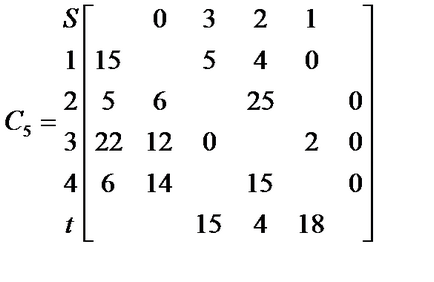
Az S és T lehetetlen megépíteni az áramkör, mert minden elem oszlopban t értéke nulla. Így megkapjuk a C mátrix *
Construct mátrix H. A negatív elemeket a mátrixban felváltja a nullák.
Σ # 1012; = 5 + 10 + 5 + 3 + 2 = 25
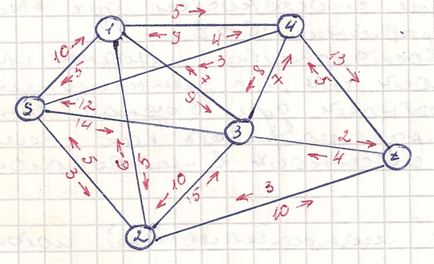
Grafikusan, a bemutatott megoldás grafikon: