Az egyenlet egy haladó hullám a fizika
Ezek az úgynevezett utazó hullámok hullámok át energiát az űrben. Energia transzfer hullámokban kvantitatívan jellemzi a vektor energia fluxus sűrűsége. Ezt a vektort nevezzük vektor fluxussűrűség. (A rugalmas hullámok - Umov).
Az elmélet az egyenlet egy mozgó hullám
Amikor arról beszélünk, a mozgás a test, azt jelenti, a mozgás a térben saját. Abban az esetben, a hullámmozgás nem a környezet vagy a változó területen, és a mozgás a gerjesztett állapot a környezet, illetve a területen. Bizonyos hullám állapot, először az egyik, lokalizált területen helyet továbbítjuk (mozog) más, szomszédos tér pontjait.
Állapota vagy a környezet a mező egy adott ponton az jellemzi, egy vagy több paraméter. Az ilyen paraméterek, például egy hullám képződik a húr, az az eltérés a karakterlánc részének az egyensúlyi helyzetből (x) a hanghullám a levegőben - a mennyiség jellemző a tömörítés vagy bővítése a levegő. egy elektromágneses hullám - egy modul vektorokat. Egy fontos fogalom minden hullám fázisban. Azzal a feltétellel, fázis érteni hullám egy adott pontban egy adott idő alatt, a megfelelő paramétereket leírt. Például, a fázis a elektromágneses hullám van állítva modulok és vektorok. Fázis pontról pontra változik. Így, CL, a fázis a hullám a matematikai értelemben, egy olyan funkció a helyzetét és az időt. A koncepció a fázis kapcsolódó koncepció a hullám felület. Ez a felület, valamennyi pont az, amely az adott pillanatban ugyanabban a fázisban, azaz Ez egy felülete állandó fázis.
A fogalmak a hullám felületre, ami egy fázis besorolás hullámok természetüknél fogva viselkedés időben és térben. Ha a hullám felületek mozognak térben (például közönséges hullámok a víz felszínén), ez az úgynevezett egy mozgó hullám.
Utazó hullámok lehet osztani: lapos, gömb és hengeres.
Egyenlet utazó síkhullámok
vagy (azonos)
ahol x lehet érteni olyan paraméter jellemző a környezet állapotának (például, az a nyomás, a hőmérséklet, stb); A- hullám amplitúdója; w- gyűrűs gyakorisága; r-távolság a forrás, a gerjesztő hullám a pontot a térben, ahol a változás tekinthető tulajdonsága a közepes, - A hullám terjedési sebessége; - kezdeti szakaszában a hullám (a referencia pont van kiválasztva). Sőt, a különböző műszakban - a hullám számot - hullámhossz; expresszió nevezzük a fázis a hullám.
Az exponenciális forma a haladó hullám egyenlet felvétel
Az exponenciális Az egyenlet alakjának (1) a formája:
ahol - a sugár vektor hívni a figyelembe vett jelenlegi környezetben; - a hullám vektor; - egy egységet vektor jelzi az irányt a hullám - komplex amplitúdó.
A (2) egyenlet meg kell jegyezni, hogy ezt a jelölést hasznos a differenciálódás a hullám egyenletek. Ugyanakkor a fizikai jelentését csak a valós része az exponenciális kifejezés.
Egyenletben szférikus és hengeres mozgó hullám
Az exponenciális formája a gömb alakú hullám egyenlet formájában:
ahol - komplex amplitúdó. Mindenütt, kivéve egy szinguláris pont r = 0, a funkció x kielégíti a hullám egyenlet.
Az egyenlet hengeres haladó hullám:
ahol r - tengelyétől.
ahol - komplex amplitúdó.
Példák problémák megoldása
A lakás akusztikai hullám izgatott csillapítatlan rezgés rezgésforrás frekvenciáját amplitúdója egy forrást. Írja egyenlet rezgésforrás x (0, t), ha kezdetben a maximális elmozdulását pontok a forrás.
Az egyenlet egy utazó hullám, tudván azt, hogy sima:
A Rögzítési egyenlet w =, levelet (1.1) a kezdeti időben (t = 0):
A feltételek ismert probléma, amely a kezdeti pillanatában legnagyobb elmozdulás a forrás pontokat. Következésképpen ,.
Kapunk. így azon a ponton, ahol a forrás (azaz r = 0).
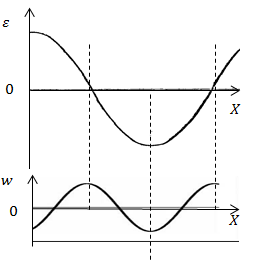
Az ábra egy grafikon, elmozdulás a hosszanti síkban haladó hullám egy bizonyos időpillanatban t. Döntetlen alapján ezt az ütemtervet példakénti grafikonja energiasűrűség W azonos időpontban t.
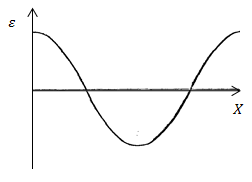
Az ábra adott a „pillanatfelvétel” a részecskék váltás a haladó hullám
Alapján a hullám minta lehet által leírt egyenlettel egyes t időpillanatban:
Abban az esetben, hosszanti síkjában a hullám energiasűrűsége kifejezve:
ahol - a sűrűsége a közeg, amelyben a hullámok terjednek, - rezgési sebessége részecske mozgást az X tengely mentén.
Behelyettesítve (2.1) a (2.3), majd (2,2), megkapjuk:
. Alapján kapott függvény Draw grafikonja energiasűrűség tolerálható hullám (ábra. 2)