Meghatározása a szögek - alkalmazási módszerek kidolgozása átalakítás - feladatainak
171 *. Határozzuk meg a szögek a vonal AB négyzetével. V és SQ. H FIS. 166, a).
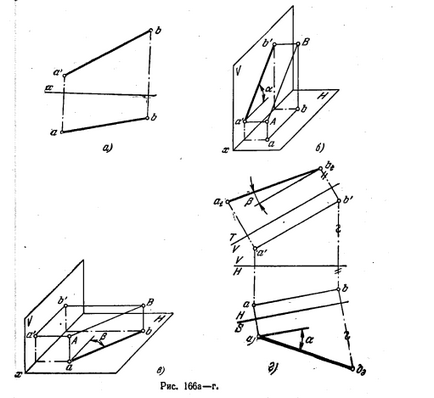
Határozat. Ha egy párhuzamos egyenes a téren. V (ábra. 166 b) közötti szög ebben a sorban, és pl. H (szög α) van ábrázolva torzítása nélkül az elülső. előrejelzések. Ha a vonal párhuzamos a téren. H (ábra. 166), a szögben, amelyet az egyenes ztoy MP. V (szög β) ábrázoltuk torzítás nélkül a horizonton. előrejelzések. Ezért, amivel egy adott vonal párhuzamos az első generikus téri. V, majd a párhuzamos MP. H, meg tudja határozni rendre a szögek és a β.
Ábra. 166 g mutat módszer alkalmazásával változások op. meghatározására a vetítési szög α és β. Így, hogy meghatározza a szöget α bevezetett további op. S, merőleges a PL. H párhuzamos és AB, és meghatározza a szög β - T ⊥ V további sík és ugyanabban az időben || AB.
Ábra. 166, stb mivel van kapcsolva egyenes: a) egy tengely körül áthaladó B pont, és merőleges a PL. H, amíg MP párhuzamosságot. V (a1 helyzetben b „a1 b.) -
meghatározott szög α; b) egy tengely körül ponton áthaladó merőleges és szögletes. V, amíg MP párhuzamosságot. H (összesen a'b'1 AB1.) - által meghatározott szög β.
Természetesen ezek a tengelyek lehet az ábrán; de úgy tűnik, a konstrukció lehetséges nélküle.
172. Dana SABCD piramis (lásd. Ábra. 154). Adjuk dőlésszögek hogy a bordák a piramis MP. V és SQ. N.
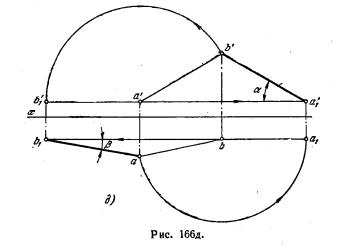
173 *. Adjuk dőlésszög által meghatározott sík háromszögek ABC (ábra. 167 is), hogy a pl. H és pl. V.
Határozat. Mint ismeretes, a dőlésszög (α) a sík MP. H vetített torzítás nélkül op. V, ha a merőleges sík pl. V (ábra. 167, 6) és a dőlésszög (β) a sík MP. V az előrejelzések torzítás nélkül op. H, ha a sík merőleges a PL. H (ábra. 167).
Ábra. 167 g, hogy folytassa a meghatározására uglaos rendszer S, H, ahol pl. S merőleges a PL. H és egy előre meghatározott síkban (tengely S / N merőleges a horizonton. 1-vetítés és vízszintes).
Meghatározása a szög β által kapcsolási rendszer V, H, hogy egy olyan rendszert T, V, ahol pl. T merőleges a PL. V és a a háromszög síkjában (T / V tengely merőleges az elülső. C2 „frontális vetítés).
Ábra. 167, stb Ugyanez a probléma a találmány szerinti eljárás megoldja a párhuzamos mozgást. Először is, az összes a csúcsokat az ABC háromszög előre meghatározott, kényszerült párhuzamos síkokban H, úgy, hogy a háromszög síkja merőleges volt a pl. V. Ez
elért horizontális A-1, mozgott úgy, hogy merőleges legyen a pl. V (horizont. A1 11 nyúlvány merőleges az x tengely). Megkapjuk a dőlésszög α az a háromszög síkjában mp. H torzítás nélkül.
Annak megállapításához, a dőlésszög β a a háromszög síkjában ABC MP. V háromszög úgy forog, hogy van elhelyezve merőleges a PL. H. Ezt útján frontális C-2: ez kerül merőleges a PL. H (összesen C2 22. Front. C'2 vetítési 2'2 ⊥ x) és így frontvl áthaladó ebben a síkban is merőleges a PL. H.
174. Dana SABC piramis (lásd. Ábra. 161). Határozzuk meg a szögeket arcok SAB, SAC és az ABC a térre. És H op. V.
175. Dan téglatest (lásd. Ábra. 165). Adjuk dőlésszög alapozzák ABCD és az arcok, hogy CDHG op. V. és arcok ADEH op. N.
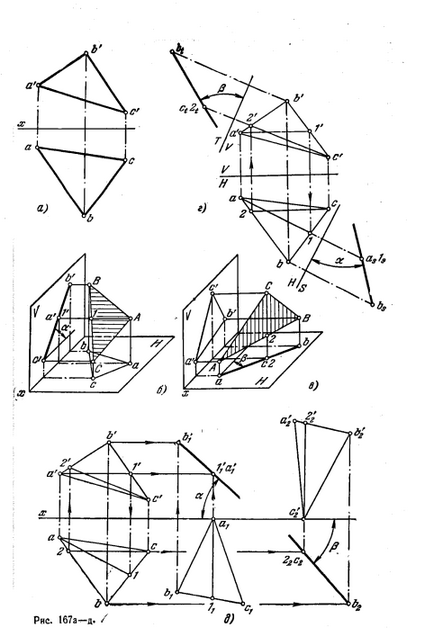
176 *. Határozza meg a szög értéke BAC (ábra. 168 is).
Határozat. Ha a szög a sík párhuzamos bármilyen op. előrejelzések, ez a szög az előrejelzések rajta torzítás nélkül (ábra. 168, b).
Ábra. 168, a probléma már megoldódott az eljárás megváltoztatja mp. előrejelzések. Mivel a gép a sík BAC szög általános helyzetben (a kontúr nem merőleges bármely síkok V, H, W), majd először is meg kell komplement rendszer V, H op. S, figyelembe merőleges az olvadáspontját. H, és a gép BAC szög. Ennek eredményeként ez az átalakulás a vetítési szög a gépen kapott S formájában szegmensek ls. Most megadhat egy további téri. nyúlványok (T), merőlegesen a vezető MP. S ugyanakkor síkjával párhuzamosan szög vas. Szög LT 2t be magukat az élet-méretű BAC szög.
Ábra. 168, és a kívánt meghatározott szög vö módon párhuzamos mozgást.
Először is, a szög a síkban mozog úgy, hogy lesz merőleges a téren. V (erre ártalmatlanítás horizonton. Vízszintes vetítési merőleges az x tengely). Aztán van egy párhuzamos síkban szöget kapunk. H, akkor lépjen a vetítési pozíció 1'1 a'1 1'2 a'2 (m. E. || x tengely). Egy másik építési ábrán mutatjuk be. 168,6. ZDS, hogy meghatározza a forgásszög körül alkalmazott vízszintes: a szög a síkban található párhuzamos op. H (T pozíció).
Az építés végre a következő sorrendben:
1. Végezze sík forgási pont - vízszintesen kiálló MP. R, merőleges a vízszintes (azaz. E. A forgástengely).
2. Ellenőrizze az AV középpontja forgási metszi a vízszintes a térre. R (G pont, G ') és a nyúlvány radiusAVrascheniya (Oa és O'A').
3. határoztuk tényleges értéke az elforgatás sugarának (ez fejezi ki a háromszög átfogója OA Oa A).
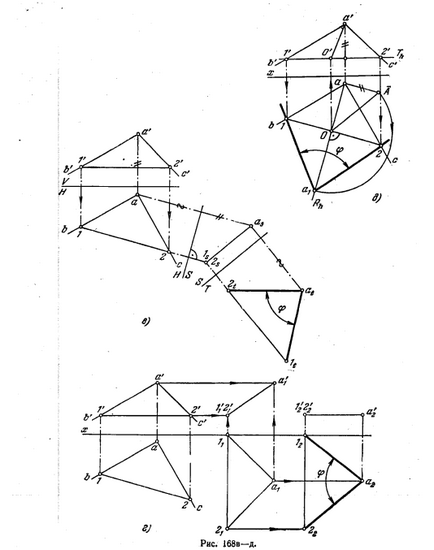
4. Töltsön az ív a kör sugara körülbelül I Rh. Megtalálni azt a pontot a1 - horizonton. vertex vetítési szög után körüli forgása vízszintesen, hogy igazodjanak MP. T - és épített 1a1 szög 2 egyenlő a kívánt.
Hogy oldja meg a problémákat, írja 176 legésszerűbb felhasználását körüli forgatás a vízszintes (vagy frontális) ábrán látható. 168, d.
177. Dana SABC piramis (lásd. Ábra. 156). Határozza meg a forgatás körül vízszintes szög a bordák között és az SB, SB és SC, SC és az SA.
178. Dan téglatest (lásd. Ábra. 165). Határozzuk meg a szög a bordák között DH és a CD, a CG, CD, AB és BC.
179 *. Nagyságának meghatározásához a ferde szög a sorok között az AB és CD (ábra. 169 is).
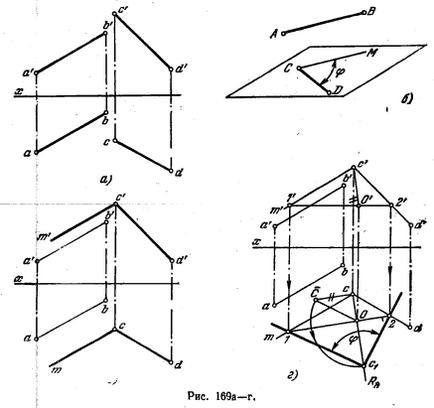
Határozat. A bezárt szög két egyenes vonal határozza ferdeségi szög szállított metsző vonalak rendre párhuzamos adat ferde. Annak megállapításához, a szög értékének meg kell kezdeni a kép rajz nr. Ez történik ábra. 169,6, és használt az egyik előre meghatározott vonalak - CD, a C pont, amely az egyenes CM párhuzamosan egy másik egyenes zadannay AB. Nagysága a szög MCD (rns.169 c) fejezi közötti szög AB és CD egyenesek. Ez úgy történik, hogy megfordult vízszintesen 1-2 (ábra. 169 a) vesszük olvadáspontja. szög MCD.
180. Dana SABC piramis (lásd. Ábra. 160). Hogy meghatározza a szöget közötti élek: a) SB és AC, b) SA és a BC.
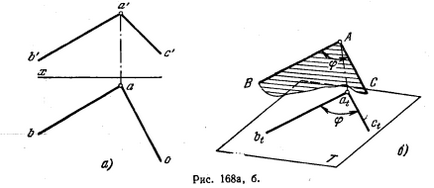
181 *. Hogy meghatározza a szöget φ hajlásszöge a vonal AB által meghatározott síkhoz háromszög CDE (ábra. 170 is).
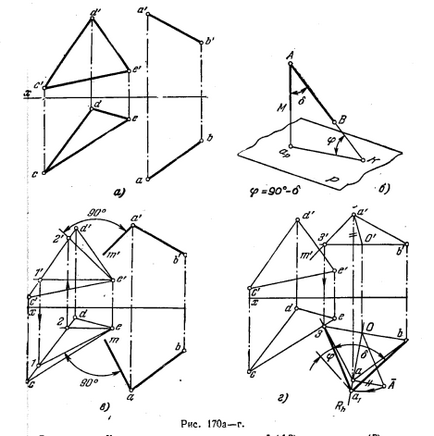
Határozat. Mint ismeretes, a szög között az egyenes vonal (AB) és a sík (P) egy akut szög (φ) a vonal és a nyúlvány (AP K) ezen a síkon. A konstrukció (ábra. 170, b) ezt a szöget meg kell találni a kereszteződésekben a téren. P AB vonal, és a merőleges levont bármely pont a vonalon AB MP. P. De ha, ahogy ez a probléma, hogy csak akkor van szükség, hogy meghatározzuk a dőlésszöget, hogy a gép a sor, akkor könnyebb nagyságának meghatározásához szög δ, kiegészítő szöge φ: megtalálni a szög δ, meg tudja határozni a szög φ a kapcsolat φ = 90 ° - δ. Ábra. 170 struktúráját szemlélteti a vetítés AM és a'm „síkjára merőlegesen a háromszög CDE, amelyeket figyelembe tsfrontal Ez a vízszintes sík: am ⊥ e - 1, a'm” ⊥ E2”.
Definiálhatjuk (ábra 170 g.) Tényleges képméret szög δ csúcsú A - történik megfordításával vízszintesen B'z”, b-3. Keresek szög φ = 90 ° -δ.
182. Dana SABC piramis (lásd. Ábra. 1611. Határozzuk meg a szögek élek SA, SB és SC a szélére AVS
183 *. Határozzuk meg a bezárt szög arcok abc és ABD (ábra. 171 is).
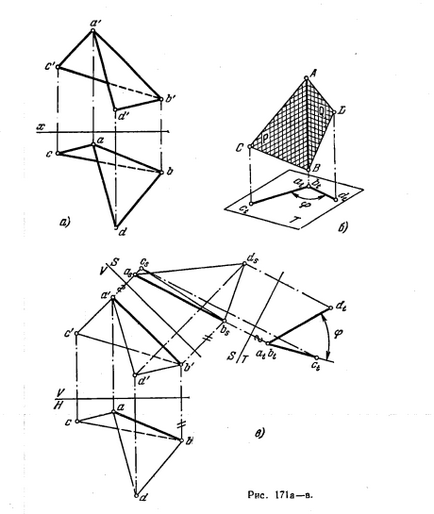
Határozat. A diéderes szöget kimérjük lineáris szöge kapott metszéspontjában az arcok az diéderes szög merőleges síkban mindkét az arcok a diéderes, és ennek következtében a metszésvonal, t. E. A szélén a diéderes szög. Ha ez az él AB merőleges lenne egy négyzet. T (ábra. 171,6) kapunk op. T vetítési diéderes szöget fejezi lineáris.
A probléma megoldása érdekében (ábra. 171, c) módszer alkalmazásával a változás pl. előrejelzések. Tól System V, H tette az átmenet a rendszer S, V, ahol S ⊥ V és S || AB, majd ebből a rendszer S, V átmenet egy rendszer T, S, ahol T ⊥ S és T ⊥ AB.
Háromszögek vetített pl.T formájában szegmensek AT AT ct és dt. A szög közöttük egyenlő a kívánt szöget φ.

Ábra. 171 g oldatot látható ugyanaz a probléma módszerével párhuzamos mozgás: AB borda szállított merőlegesen pl. N.
184 *. Határozza meg a szög értéke által képzett P sík és a sík ABC háromszög (ábra. 172 is).
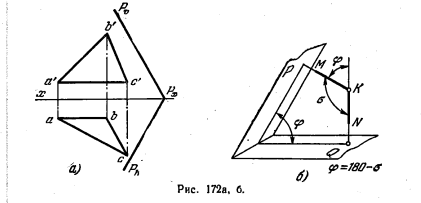
Határozat. Ha a probléma megoldásához kövesse a rendszer a korábbi megoldások, ki kell építeni egy metszésvonala az adott síkok. De meg tudod csinálni egy másik dolog, anélkül, hogy az építési ezt a sort, ez van. E. megadása nélkül a széleit a kívánt torziós szög. Akkor a következőképpen kell eljárni: nem közvetlenül meghatározza a szöget φ, és az a szög σ (ábra 172, b.) És a függőlegesek közötti KM KN, pontig húzott K, az előre meghatározott síkra. Miután megtaláltuk a szög σ, megkapjuk φ = 180 ° - σ.
Ez a megoldás eltér a lényege a megoldásokat ábra szerinti. 171 és 171 a. Figyelembe a K pont (ábra. 172, c) levonni merőlegesek, és KM KN rendre az a háromszög síkjában ABC n PL. P: a K 'tartsa k'n' ⊥ A'B 'és k'm' ⊥ Pϑ. de a lényeg k - kn ⊥ ac és km ⊥ Ph. Az így kapott szög kiemelkedések és MKN n'k'n „(σ szög) .Naturalnaya ezt a szöget kapunk forgatásával vrkrug frontális 1-2 (ábra. 172 g). Mivel a hegyesszög kapunk, ez lehet
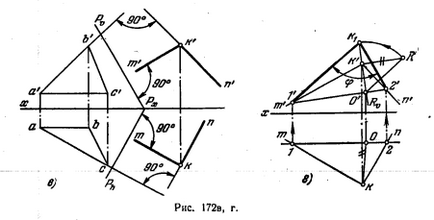
feltételezzük, hogy ez határozza meg a kívánt szöget az előre meghatározott arc, mivel a sarkok a szomszédos kapott kölcsönös metszi a két sík, szögek, a síkok közötti tekinthető éles.
185. Dana SABCD piramis (lásd. Ábra. 154). Határozza meg a módszer megváltoztatja a síkja vetítési szög közötti arcok SAB és SBC, SBC és SCD, SAD és SAB.
186. Dan paralelepipedon (ábra. 165). Határozzuk meg a szögeket a lapok közötti CDHG és EFGH, BCGF és CDHG.