Bevezetés, elméleti rész - létrehozását mini-játékok - a bűvös négyzet
A téma a kutatási munka létrehozása „mini-game” bűvös négyzet „” Lettem érdekelt a létrehozásának ötlete egy matematikai minigames. Elérhető rám Pascal programozási nyelv ismerete nem volt elég, de, mert nem teszi lehetővé, hogy hozzon létre egy programot egy vonzó és felhasználóbarát felület. I szembe két probléma: 1) módszerek töltse egy négyzetes mátrix; 2) választott programozási nyelv végrehajtása a játék. Az első probléma könnyen megoldható tanulmányozása után a szakirodalom. A második dolgoznom kellett. Azt választották Delphi programozási nyelv, a kernel, ami a Pascal. Tanult a szakirodalom támogatott online fórumok bizonyos kérdésekben.
A munka fontos azoknak, akik szeretnék kezdeni mastering a Delphi programozási nyelv. Népszerű bölcsesség azt mondja: „nem lehet tanítani senkinek semmit, de lehet tanulni.” A „bűvös négyzet” példája létrehozása mini-játékok segítségével megtanulják, hogyan kell használni komponenseket az eljárás végrehajtásához változtatni a tárgyak tulajdonságait, kezelni az eseményeket. A gyakorlati jellegű ismeretek - a leghatékonyabb tanulási forma.
Számomra ez a munka egy nagy lépés a tanulmány, és ami a legfontosabb, a gyakorlati alkalmazása a magas szintű programozási nyelv.
A kutatás tárgyát a programozási nyelv Delphi.
Kutatás tárgya - fejlesztési programok létrehozására mini-játékok Delphi programozási nyelv.
A vizsgálat célja az volt, hogy:
elméleti alapjait és fejlesztési program egy mini játék „mágikus négyzet”.
# 118; elemzik a célját és lehetőségeit Delphi;
# 118; megvizsgálni, hogyan lehetne megoldani a problémát a teremtés Delphi mini-játékok;
# 118; dolgozzon ki egy programot a „Magic Quadrant” mini-játékok
Ez lesz az
W fejlesztése és alkalmazásai programozási ismeretek;
W programozási ismeretek a népszerű Delphi programozási rendszer;
W informális asszimiláció az anyag a programozási nyelv Delphi.
Összhangban a cél és hipotézis a vizsgálatban megállapított, és megoldották a következő feladatokat látja el:
Írjunk programot, hogy hozzon létre egy „bűvös négyzet” mini-játékok, amelyek egyrészt generál területén bűvös négyzet 3 # 63; 3, néhány üres cellák; másrészt ellenőrzi, hogy tele négyzetes mátrix „mágikus” tér.
Bűvös négyzet, négyzetes elrendezés az egész számok, amelyben a számok összege minden egyes sor mentén, minden oszlopban és minden a két fő átlók egyenlő ugyanazt a számot.
Bűvös négyzet - az ősi kínai eredetű. A legenda szerint uralkodása alatt császár Yu (c. 2200 BC), a Sárga-folyó víz (Sárga-folyó) alakult szent teknős shell, amelyen a titokzatos hieroglifák voltak írva (1A.), És ezek a jelek néven Lo Shu bűvös négyzet, és ekvivalens a ábrán látható. 1b. A 11. században. mágiáról négyzetek megtanulták Indiában, majd Japánban, ahol a 16. században. magic square kiterjedt irodalomban. Az európaiak be mágikus négyzetek a 15. században. Bizánci író E.Moskhopulos. Az első négyzet feltalált Európai tekinthető Durer square (ábra. 2) mutatja be a híres gravírozás melankólia 1. Alapítva metszetek (1514) tartalmaz, a számot a két központi sejtek az alsó sorban. Bűvös négyzetek különböző tulajdonított misztikus tulajdonságokkal. A 16. században. Cornelius Agrippa Heinrich épített terek 3., 4., 5., 6., 7., 8. és 9. megbízásokért járó asztrológia 7 bolygók. Gyakori hiedelem, hogy vésett ezüst bűvös négyzet véd pestis. Még ma is láthatjuk a mágikus négyzetek az európai jövendőmondók attribútumokat.
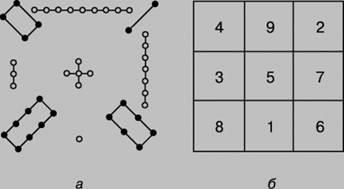
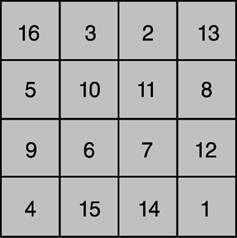
A 19. és 20. században. érdeklődés a bűvös négyzet tört újult erővel. Ők kezdték felfedezni módszerekkel algebra és az operatív kalkulus.
Minden eleme a bűvös négyzet van a cella. Tér, az oldalán, amely áll N sejtek, amely 2 n sejtek és az úgynevezett négyzet n-ed rendű. A legtöbb mágikus négyzetek használnak első n egymást követő egész szám. Sum S számok minden sorban és minden oszlopban sem a diagonális négyzet nevezzük állandó és egyenlő az S = n (n 2 + 1) / 2. Bebizonyosodott, hogy n # 63; 3. Egy négyzet a sorrendben 3 S = 15, 4. érdekében - S = 34, 5-edrendű - S = 65.
Két átlós áthaladó a tér közepén, az úgynevezett fő átló. Bent úgynevezett átlós, amely, mielőtt elérik a szélén egy négyzet, párhuzamosan húzódik az első szegmens a szemközti élen (alkotnak egy átlós sötétített cellák ábrán. 3.). Sejtek, amelyek szimmetrikusak az a tér közepén, az úgynevezett ferde. Ilyenek, például sejtek a és b ábrán. 3.
Ábra. 3. Lohmann Átlós és ferde SEJTEK
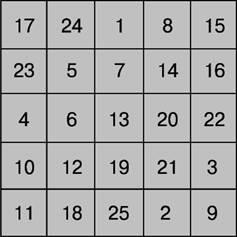
Páratlan érdekében mágikus négyzetek lehet kialakítani módszerével francia geométert 17. A. de la Lubero. Tekintsük ezt a módszert, mint például négyzetes rend 5 (ábra. 4). Az 1-es szám kerül a főtér a felső sor. Minden természetes számok találhatók a természetes rend ciklus alulról felfelé a sejtekben átlós jobbról balra. Miután elérte a felső szélén egy négyzet (mint abban az esetben, 1), továbbra is töltse az átlós, kezdve az alján a következő oszlop sejtek. Amikor elérte a jobb szélét a tér (3-as szám), folyamatos, hogy kitöltse a átlósan elhelyezkedő balról fenti sejtvonal. Elérése a töltött sejteket (5-ös szám), vagy a szög (szám 15), az út le az egyik cella lefelé, majd a töltési folyamat folytatódik.