3. téma koncepció Fredholm rezolvens integrál egyenlet, szabad dolgozatok, esszék és

abban az esetben,

és. ahol

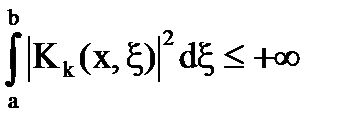
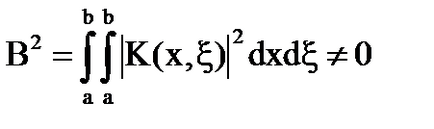
Ez adja meg:

Mivel a sorozat (19) konvergál egyenletesen, lehetséges, hogy a sorrendet a összegzési és integráció:

Jelöljük - Neumann sorozat. (23)

Ez a funkció az a felbontás az (1) egyenlet. Az egyenlet megoldása felírható:

Ha a számított felbontás, az oldatot lehet írva egyszer ().

Definíció: Azt mondjuk, hogy az integrál egyenlet (1) van egy felbontása R (x, # 958, # 955;), ha az oldat az egyenlet felírható (24), és ez a megoldás egyedülálló minden szabad távú f (x).

Nyilvánvaló, hogy ha van egy felbontása integrál egyenlet, ez egyedülálló.

Sőt, még akkor is, ha. egyenletnek két állásfoglalások és. Akkor az egyetlen megoldás az egyenlet felírható:

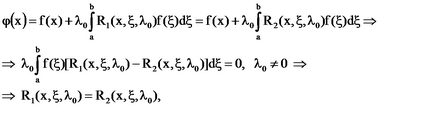
mert f (# 958) - egy tetszőleges függvény.

Megjegyzés: A felbontás meghatározásra került csak értékeket # 955;, úgy, hogy. Van azonban egy állásfoglalást az egész komplex síkon # 955;, kivéve néhány elszigetelt értékeket # 955;.

. ;

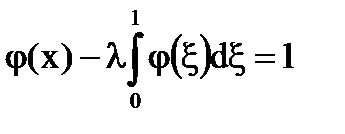
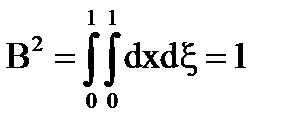
Neumann sorozat konvergál az | # 955; |<1.

kifejezetten # 955; ≠ 1 (belül és kívül a körön | # 955; | = 1, a kör, kivéve a csak # 955 = 1).

Megjegyzés: Bizonyos Fredholm egyenletek a sorozat (23) konvergál az összes # 955;.

Tegyük fel, hogy

. Találunk egy becslést az iterált mag, az a tény, hogy

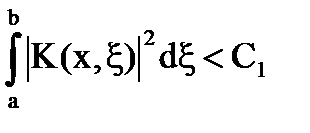
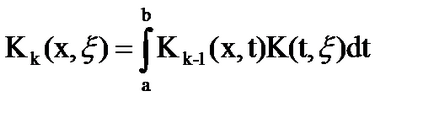
Azáltal Cauchy - Schwarz:

integrálása # 958;, megkapjuk

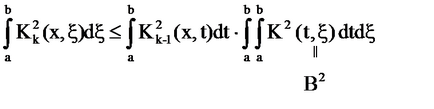
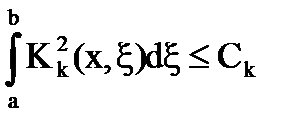
Itt van. tehát

Ennélfogva, a sorozat konvergál.

Ezért a felbontás megfelel a következő integrál egyenlet:

Ez az integrál az úgynevezett «k» -ik mag nyoma vagy a nyomokban «k» i-edik kernel iterált. Van x = # 958;

Miután integrációja x az [a, b]:

Példa. Construct rezolvens formalizmus segítségével iterált magok.

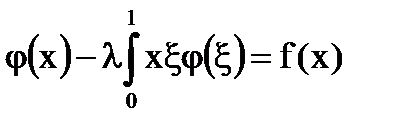
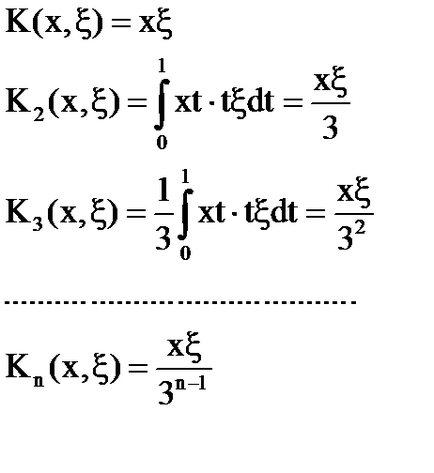
A megoldás az integrál egyenlet:

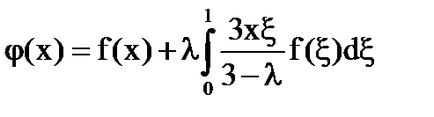
gyakorlatok:

Keresse meg a kernel megismételhetjük mondta sejtmagokat meghatározott és b

és építeni egy felbontást.

Építőipari határozatok az alábbi magok