Math vs. józan ész
A matematika, létezik jó néhány példát helyzetek is létezik a valóságban, de nincs logikus magyarázat, és így tesz minket teljesen leállt. Az alábbi kapcsolódó feladatok valószínûségelmélettel nem engedi, hogy unatkozni, és segíteni fog, hogy tesztelje a szellemi kapacitás.

Képzeld el, hogy részt vesz a show, ahol gazda megmutatja, három ajtó. Mögött az egyik ajtó egy díjat - egy új autót, de a fennmaradó 2-2 kecske. Választhat bármilyen ajtót, és hogy pontosan a díjat, hogy mögötte van.
Ön választja ki az ajtót, majd vezető megnyitja az egyik a másik két ajtó (master tudja, hol az autó rejtett, de mindig kinyitja az ajtót, ami mögött egy kecske).
Lead megkérdezi:
- Akarsz változtatni a kiválasztási? Vagy megáll ugyanabban az ajtó választja?
A megoldás?
Ezért úgy dönt, hogy a jelenlegi beállítás választása.
Végtére is, nincs különbség, a változás az ajtót, vagy sem. Mivel már csak két ajtó, a lehetőséget, hogy hiszem, ha a gépet 50/50. Jobb?

A helyes válasz: mindig változik a választás, mert akkor a nyerési valószínűsége az autó lesz kétszer annyi.
Az a játékos, akinek stratégia az lenne, hogy minden alkalommal, amikor változik a kiválasztott ajtót fog játszani csak abban az esetben, hogy ő eredetileg úgy dönt, egy ajtó, ami mögött egy autó. Mivel a választásának valószínűségét az autó az első kísérlet a 1-3 (vagy 33%) esélye, hogy ne válasszon egy autót, ha a játékos megváltoztatja a választás, szintén megegyezik 1-3 (vagy 33%). Ez azt jelenti, hogy a játékos, aki a stratégiát változtatni az ajtót, hogy megnyerje a valószínűsége 66%, vagy két-három. Ez megduplázza a nyerési esélyeit a játékos, akinek a stratégia - minden alkalommal, hogy nem változik a választás.
Még mindig nem hisznek? Tegyük fel, hogy úgy döntött, az ajtó №1. Itt megtalálja az összes lehetséges opciót, ami történhet ebben az esetben:

Ha elhagyja a kezdeti választás, akkor megnyeri az egyik háromszor; ha van egy választás - tippelni háromból két alkalommal.
Még mindig nem biztos? Csináljuk ugyanezt, csak a 50 ajtók. Ön választja ki az ajtót №1.
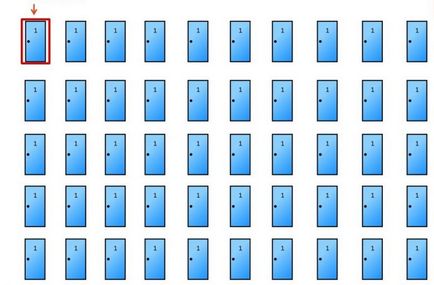
És mi nyissa meg a többi 48 ajtó, ami mögött rejtett a doboz. Ön abban a választásban? Ne feledje, hogy 1 esélye 50 kitalálni a kívánt kaput az első kísérlet. Úgy működik, ugyanezt az elvet.

V: Annak valószínűsége, hogy két ember az irodában születésnapját esik az ugyanazon a napon, 50%.
Ha a számjegyek száma egy személy eléri 366, a statisztikailag biztosította, hogy legalább két ember Születésnapokat egybeesnek, hiszen lehet, csak 365 lehetséges születésnapokat. Azonban, ha figyelembe vesszük, hogy minden születésnapok egyformán valószínű, hogy egy csoport 57 fő a valószínűsége egy ilyen egybeesés lenne 99%.

Hogyan találjuk ki?
Térjünk vissza a 23 kollégák az irodában, hogy megértsük, hogyan vozmozhno.Sformuliruem fordítottja: nincs két ember a csoport mérkőzés nap rozhdeniya.Vyyasnit valószínűsége, hogy legalább két ember az irodában ünnepelte a születésnapját aznap, ez nagyon nehéz, ha közvetlenül szembesülnek etim.Vyyasnit valószínűsége annak, hogy senki sem az nem egyezik a születésnapokat csoport sokkal könnyebb.
Annak a valószínűsége, hogy két ember nem ugyanaz a születésnapokat, az alábbiak szerint:
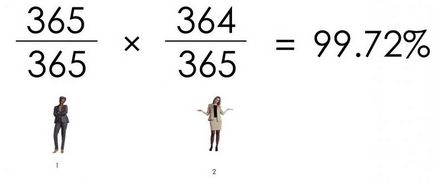
Annak a valószínűsége, hogy nem felelnek meg a születésnapokat három ember:
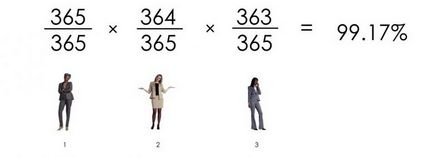
Annak valószínűsége, hogy a négy férfi nem azonos a születésnapokat, az alábbiak szerint:
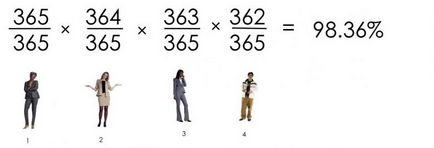
Látod, amit kapunk? Annak valószínűsége, hogy 23 ember születésnapok nem ugyanaz, a következő:

Mivel az esélye annak, hogy senki sem született ugyanazon a napon, 49,3% az esélye, hogy legalább két ember azonos születésnapját, egyenlő 50,7%.
Itt látható a görbe valószínűsége:
Ez a csapat már átlagosan 2,85 barátok tiszt. Ugyanakkor az átlagos barátok száma, akik barátai a barátok az ember 3.39.
Ezek az emberek voltak azok az átlagos barátok száma, a fentiek szerint. Ennélfogva ezek a legnépszerűbb tagja a csapatnak. De a legfontosabb az, hogy 17 a 20 ember az irodában barátok, legalább egy ilyen ember:
Egy rab izgatott, mert most a túlélési valószínűség 1/2 helyett 1/3, mint az egyik fogoly, A vagy C, majd pomilovan.Zaklyuchonny Egy rab titokban mondja C, hogy a B lesz végrehajtva. A fogoly is izgatott, mert még mindig úgy véli, hogy a túlélés valószínűségét egy fogoly A 1/3, és a túlélés valószínűsége nőtt 2/3.
Melyikük a baj?
Válasz: S. fogvatartottak jogainak
1) Kezdetben mindhárom fogoly egy lehetősége van három kegyelmet. Az őr azt mondta, hogy fogoly B lesz végrehajtva, ami azt jelenti, hogy az események bontakozik ki egyik két forgatókönyv:
- C megbocsáttatott (1 esélye 3)
- A megbocsátott és érme mutatott „B” (1 esélye 6-ból)
2) Ez azt jelenti: az esélye, hogy egy fogoly kegyelmet És felét teszik ki a lehetőséget, hogy a C lesz megkegyelmezett. És a fogoly nincs esélye, hogy megkegyelmezett.
3) Így a valószínűsége, hogy egy a kegyelmet is hiányzik - 1/3, míg annak valószínűsége, hogy a növekedés kegyelmet 2/3.
Ha még mindig kétséges, hogy egy pillantást a teljes listát odds minden fogoly:
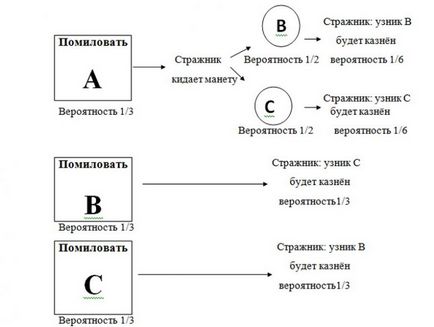
És ha megnézi egy példát, ahol az őr jelentette, hogy a fogoly kerül végrehajtásra, azt látjuk, hogy a fogoly C kétszer az esélyét, hogy kegyelemben, mint fogoly A:
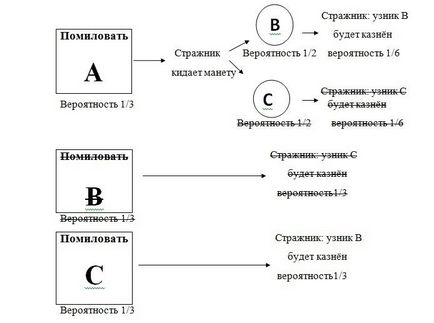
Tehát hogyan tudjuk biztosan, hogy a 0% az esélye, hogy megkegyelmezett, és hogy C kétszer az esélyét, hogy megkegyelmezett helyett, akkor:
Az őr azt mondja, hogy a B lefut

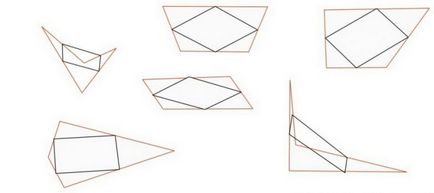
5. A tökéletes paralelogramma sokszög négyoldalú
Rajzolj egy négyszög sokszög.
Ez lehet bármilyen méretű, szabálytalan alakú, konkáv, konvex, és így tovább. D. A lényeg az, hogy a négy sarka és egyenes oldala van.
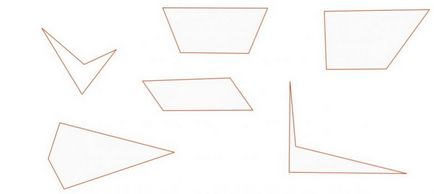
Megjegyzés középső pont mindkét oldalán a sokszög.
Csatlakoztassa a középpont között. Minden alkalommal, akkor már nyert egy tökéletes paralelogramma.