elméleti leírása
A szabad úthossza molekulák l nevezett által megtett átlagos távolság a molekula két egymást követő ütközés más molekulákkal.
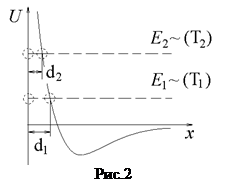
Következésképpen, a hatásos átmérője a molekulák növekvő hőmérséklettel csökken. Azonban, a változás a d a hőmérséklet növekedésével enyhén. Az érték az úgynevezett effektív keresztmetszet a molekula.
Molekuláris gázok kinetikus elméletét vezet a következtetést. Az átlagos szabad úthossz fordítottan arányos l koncentrációban n a hatásos keresztmetszeti a molekula
Ez a képlet olyan látható fizikai jelentése: az átlagos szabad úthossz kisebb, a vastagabb elhelyezett molekulák (azaz nagyobb mint n) és a nagyobb átfedett az egyes molekulák (azaz nagyobb mint s).
Állandó hőmérsékleten arányos a sűrűsége a n molekulák gáznyomás. Következésképpen, az átlagos szabad úthossz fordítottan arányos nyomás:
.
Csökkenése miatt a hatásos átmérője a molekuláris szabad úthossz a hőmérséklet növekedésével enyhén növekszik.
L intézkedés gyakorlatilag lehetetlen, de miután l kifejezett összes közlekedési együtthatók, amelyek viszonylag könnyen mérhető a kísérletben.
A dinamikus viszkozitást a gázok a következőképpen fejezhető ki: (2)
ahol - az átlagos sebesség a gáznemű molekulák, R - a gáz sűrűsége.
Először meg kell mérni a viszkozitás órán át, majd a (2) képlet kiszámítja az átlagos szabad úthossz l, és végül az (1) képletű vagy a kiszámítására s d.
Ami a tapasztalat, szükséges, hogy válasszon egy fizikai jelenség, amely lehetővé tette egy egyszerű módja annak, hogy az intézkedés a viszkozitás a levegő.
Ebben a munkában, mivel egy ilyen jelenség egy viszkózus levegő áramlását a kapilláris.
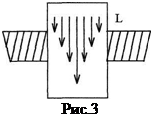
Ha a kapilláris ér véget, hogy hozzon létre egy nyomáskülönbség. fordul elő a kapilláris viszkózus légáram, amelynek sebesség profil a 3. ábrán látható. Során t rajta áramló levegő mennyisége V, amely lehet kiszámítani Poiseuille:
ahol - a kapilláris sugara, - a hossza.
A nyomás-különbség a végén a kapilláris van beállítva az a tény, hogy a szelepen keresztül a henger K tömítetlen.
Szükséges, hogy a víz folyt csepp. Ezután a levegő-munkahenger nyomását, és a hidrosztatikus nyomás a folyadék oszlop magassága h ellensúlyozni a légköri nyomás, azaz F
,
Mivel h lassan változik, és a változás lineáris, akkor a (3) képlet helyettesíteni kell a középérték
Másrészt, a levegő térfogata áthaladó kapilláris térfogat folyóvíz, amely könnyen meghatározható a következő képlettel
.
Ezért kell mérni a nagyságát 4: V, T, H1 és H2. Ezután a következő képlettel (4), és h a (3) képlet.
Továbbra is számítani l, és d. Ehhez számos transzformációs kezdeti képletek (1) és (2).
Tekintettel arra, hogy és. formulából (2) találunk
Ettől. Az (1) képletű van:
Az összes képlet - a kapilláris sugara, - a hossza a kapilláris, S - keresztmetszeti területe a hajó vízzel = 1000 kg / m 3 - a víz sűrűsége, R = 8,31 J / mol K × - egyetemes gázállandó, k = 1,38 × október 23 J / K - Boltzmann állandó, m = 0,029 kg / mol - moláris tömege a levegő, g = 9,8 m / s 2 - szabadesés gyorsulás, T = (T + 273) K
1. Határozza meg a szabad úthossza a molekulák.
2. Hogyan működik az átlagos szabad úthossz a hőmérséklet?
3. Hogyan működik az átlagos szabad úthossz állandó hőmérséklet, a nyomás?
4. Mi az effektív átmérője a molekulák?
5. Mi határozza meg az átlagos szabad úthossz molekulák és a tényleges átmérő ebben a munkában?
6. Mi az úgynevezett migrációs jelenségek?
7. Mi a viszkozitás vagy a belső súrlódás?