A megoldás a lineáris programozási feladatok révén excel programot
Lab № 1
Cél: tanulmány a modern szoftver megoldása lineáris programozási feladatok; gyakorlati problémamegoldás lineáris programozás grafikus módszerrel, szimplex módszer, és lehetővé programmyMicrosoftExcel; szoftver megvalósítása a szimplex módszer, magas szintű programozási nyelv.
1. Az elméleti rész
Megoldására lineáris programozási feladatok Microsoft Excel Solver áll, amelyek elérhetik az Eszközök menüben.
Ha a csapat a megoldás keresésére nem az Eszközök menüben. hogy szeretné telepíteni a bővítményt „Megoldások”. -Kiegészítők ezt a parancsot az Eszközök menüben. amely megnyitja a párbeszédablak ábrán látható. 1.
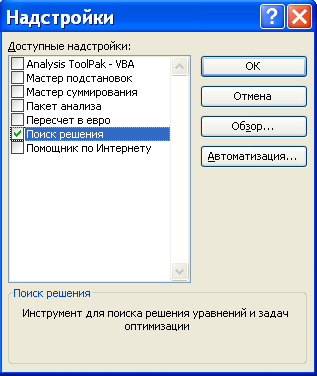
A többi ezt a box set doboz a bővítmény a betölteni kívánt, majd nyomja meg az OK gombot.
Megmutatjuk a használata kiegészítői „A keresés megoldás” a példa megoldása a következő probléma.
Nyilatkozat a problémát
A cég gyárt és értékesít három termék - P1. P2 és P3. Mert gyártás során háromféle erőforrás - alkatrészek és alapanyagok. Készletek az erőforrások és hasznosításuk a termelés egységnyi termelési fajonként táblázat tartalmazza. 1.
Profit eladásából származó egységek minden típusú 240, 210 és 180 pénzegység P1. P2 és P3, ill.
Szükséges, hogy meghatározzák a vállalat termelési program oly módon, hogy hasznot termékek értékesítésének volt a legmagasabb.
A matematikai modell a probléma
Jelöljük x1. x2 és x3 kívánt mennyiségek P1 típusú termelés. P2 és P2. és ezen keresztül az F - profit vállalkozások. Ezután a matematikai megfogalmazása a probléma, amelyet a következő űrlapot.
Határozzuk meg az értékeket az x1. x2 és x3. amelyek esetében a maximum a célfüggvény
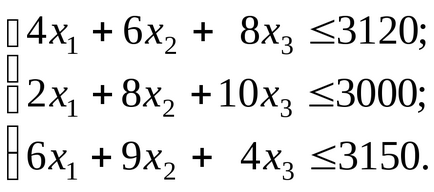

A célfüggvény leírja a teljes nyereség értékesítéséből származó mindhárom kimenet. Korlátozások (1), (2) és (3) lehetővé teszi az áramlás és a készletek az alkatrészek és nyersanyagok, ill. Mivel a gyártási mennyiség nem lehet negatív, hozzáadunk feltételek
X1 ≥ 0; x2 ≥ 0; x3 ≥ 0. Az eljárást az optimális megoldás
Példaértékű cselekvések megoldásához szükséges lineáris programozási feladatok révén Excel képviseletében a lépések sorozatát.
1. lépés: a feladat elindítása adat van írva a munkalapra táblázatot. Az egyik lehetőség ábrán látható. 2.
Megjegyzés. Ha tudja, hogy az eredeti elfogadható alap megoldás, akkor lehet kissé felgyorsítja a folyamatot az optimális megoldás. Ehhez a kiindulási értékeit néhány vagy az összes változót kézzel lehet beállítani. Ebben a példában, ezeket használják tárolására sejtek $ B $ 2, $ C $ 2 és $ d $ 2. Ha érvényes lúgos oldatot nincs megadva, az Excel automatikusan meghatározza a kezdeti változók értékét a probléma.
2. lépés A cellát bevezetésre E3 képletű
kiszámításához az aktuális érték a célfüggvény, amely megállapítja az összege páros termékek sejtek (B3: D3) az együtthatók a változók tekintetében a célfüggvény a sejteken ($ B $ 2: $ D $ 2) a változók aktuális értékei.
3. lépés a határokat a probléma, a sejt-E5, E6 és E7 másolt a képlet a cellába E3. Ezt követően, ezeket a sejteket kell készíteni képletű táblázatban látható. 2.
4. lépés létrehozása után a tábla mutató van beállítva, hogy a kezdeti adatok E3 tartalmazó sejt kiszámításának képletét a célfüggvény. Ezután a csapat a megoldás keresésére van kiválasztva az Eszközök menüben. amely megjelenik egy párbeszédablak, ábrán látható. 3.
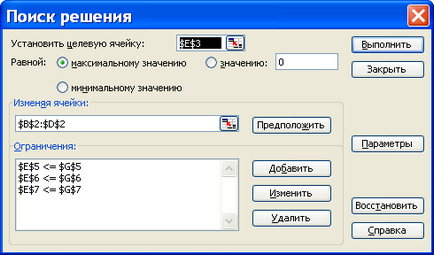
Ezután az ablakban (. 3. ábra) vannak töltve a következő mezőket ebben a képernyőn:
- egy kapcsoló mezőt alkotnak extrémuma a célfüggvény van állítva a maximális értéket (vagy minimális értéke, amikor egy megfelelő kiszerelés a probléma);
- A cella szerkesztése megadott tartomány a sejteket a változók értékeit a kiosztott feladatok a munkalapot táblázatkezelő (a példában a cella $ B $ 2: $ D $ 2);
- Korlátozások a területen, hogy állítsa be a megszorítások az eredeti probléma. Ehhez a kurzort a beviteli mezőbe korlátozásokat, és kattintson a Hozzáadás gombra. Ennek eredményeként a kiadási hozzáadása „kényszer” párbeszédablak ábrán látható. 4.
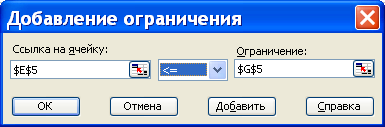
Ezután válassza ki, hogy milyen típusú kapcsolatok összekötő jobb és bal oldalán a korlátozások, ábrán látható. 5.
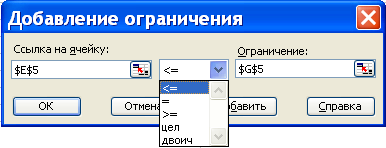
Miután a Hozzáadás gombra kattintva a „Hozzáadás a megszorítás” (vagy az OK gombot az utolsó korlátozások), ez a korlátozás szerepel korlátozások feladathoz. Nyomda törlése és szerkesztése, törölheti a listában kijelölt korlátozások, vagy hogy a korrekciókat.
Megjegyzés. A „hozzáadása a megszorítás” jelezheti, hogy néhány vagy az összes változót kell bevenni egész értékeket (5.). Ez lehetővé teszi a megoldása egész lineáris programozás (teljes egészében vagy részben) integrál.
5. lépés: Ha az összes mezőt az ablak „Search megoldás”, nyomja meg az Options (3.), Amely megnyitja a „Részletes keresés Solutions” párbeszédablak ábrán látható. 6.
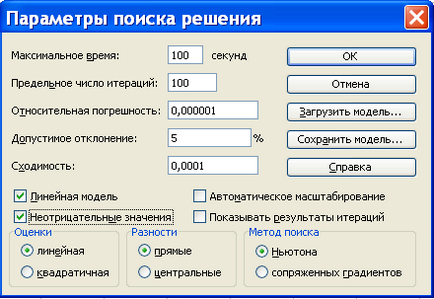
Ebben az ablakban szeretné telepíteni a dobozok lineáris modell megoldására lineáris programozási feladatok, és nem negatív értéket, ha egy ilyen feltétel kivetett összes változó a probléma.
Itt is (. 6. ábra) is megadhatjuk a paramétereket a döntési folyamat: a limit idő keresési megoldások maximális iterációk száma, pontosság, stb Ellenőrizze megjelenítése rezultatyiteratsy lehetővé teszi a lépések a megoldások megtalálásához. Autom.zoom jelölőnégyzetet aktiváljuk abban az esetben, ha a tartományban változók értékei nagyon nagy.
6. lépés Állítsa be a szükséges paramétereket a „Részletes keresés megoldások”, nyomja meg a Run gombra keresni a megoldást a problémára (3.) És a „Keresés a megoldást.” Ha megoldást nem találnak, akkor a képernyőn megjelenik a megfelelő üzenet (7.).
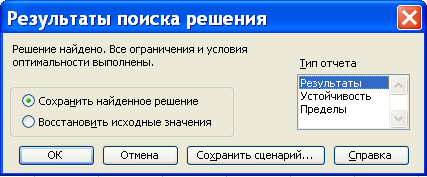
Az eredmények megjelennek a munkalapon, táblázatkezelő, ábrán látható. 8. Különösen a változók értékét - a sejtekben $ B $ 2: $ D $ 2, az értéke a célfüggvény - cellában E3.
Így a kapott optimális megoldás az eredeti probléma, mint egy vektor, ahol a
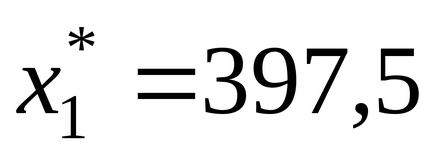
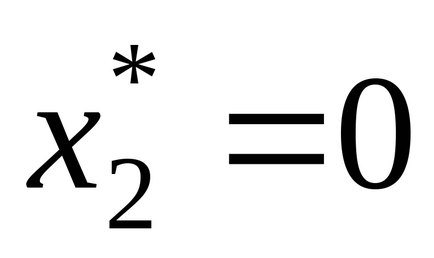
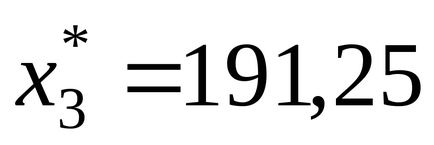
Az eredmények megoldani egy lineáris programozási feladat is lehet megtakarítani, mint külön munkalap megnevezett Jelentés az eredményeket a fenntarthatósági jelentés és a jelentés határai. Hogy mentse az eredményeket a jelentések, akkor először, a jelentés típusát jelölje ki a kívánt jelentést típusok (7.). Ebben az ablakban megadhatja, hogy nem kap a döntések és visszaállítja az eredeti változók értékét.
az eredmények a jelentés a figyelmet a probléma ábrán látható. 9.
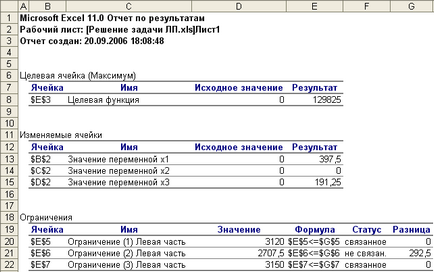
Ez a jelentés az optimális megoldás a lineáris programozás és a helyét a területen megvalósítható megoldásokat. Az eredmény megjelenik a grafikonok az optimális értékek a célfüggvény F * és a változók a probléma
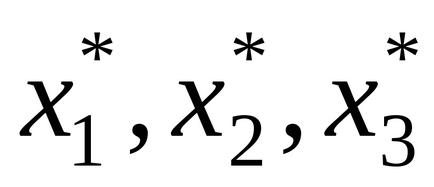
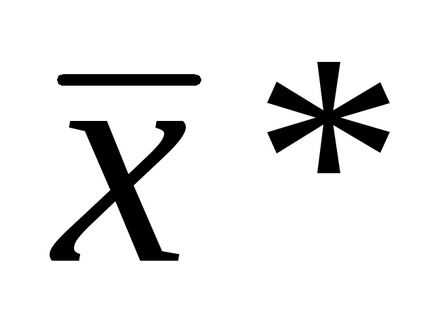
Megjegyzés. A gazdasági értelmezése a kapcsolódó korlátozások megfelelnek a szűkös erőforrásokat. A nem-korlátozása a grafikon azt mutatja, a különbség a fennmaradó mennyiségű kihasználatlan erőforrások nem szűkös. A probléma tekinthető korlátozások (1) és (3) megfelel a komponensek és anyagok, amelyek szűkös erőforrások. Constraint (2) nem kapcsolódik, vagyis Ez nem befolyásolja az optimális terv termelési kritériuma szerint a maximális profit. Ez azt jelenti, hogy a második forrás (nyersanyag) használjuk fel a mennyisége 292,5 egységek.
A jelentés a stabilitását (10.) Mutatja a változók a probléma a stabilitási határ (oszlopok megengedhető növekedés vagy csökkenés megengedhető együttható a célfüggvény), valamint a stabilitás a határ árnyék árak (azaz a változók a kettős probléma), amelyen belül az optimális megoldás nem változik. A nagy értékek a határértékek (1E + 30) jelenti a tényleges hiánya megfelelő határfelületei, vagyis változó lehet változtatni a végtelenségig.
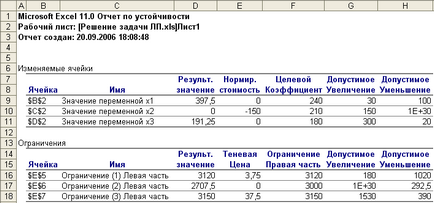
Az oszlopot normalizált értékét az elem a második sorban (-150) azt mutatja, hogy mennyi az értéke a funkció csökkent, ha a döntési változó x2 értékét növeli. Másrészről, egy elfogadható növekedése az együttható ismeretlen funkciójú x2 150 egység, ez a változó nem változik, azaz, ismeretlen x2 értéke nulla, és mikor kell túllépni a megengedett növekedés (x2 növelése együtthatója több mint 150), akkor az ismeretlen x2 a megoldás az lesz, nagyobb, mint nulla.
A jelentés a határértékek (ábra. 11) azt mutatja, az alsó és felső határok lehetséges variáció a változók (területén belül megvalósítható megoldásokat), és a megfelelő célfüggvényértékek (oszlop Cél eredmények) ezeket a változásokat. Különösen, ha X1 = 0, és X2 és X3 változatlan marad, akkor F = 2400 + 2100 + 180191,25 = 34425; x3 = 0, ha és állandó x1 és x2 kapjunk F = 240397,5 + 2100 + 1800 = 95400.