A függvény y k
Tekintsük az y = k / y. Grafikonja ez a funkció a sorban az úgynevezett matematikai túlzás. Az általános formája a hiperbola az alábbiakban bemutatjuk. (A grafikon azt mutatja, a funkció y k-val egyenlő osztva x, y, ahol k egyenlő egy.)
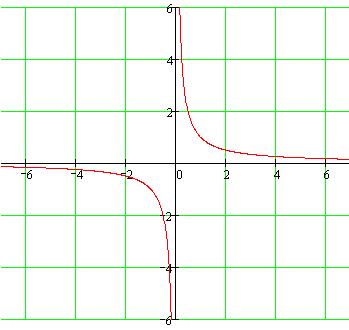
Látható, hogy a grafikon két részből áll. Ezeket a részeket nevezzük ágai a hiperbola. Azt is meg kell jegyezni, hogy minden ága a hiperbola illeszkedik egyik irány egyre közelebb és közelebb a koordináta tengelyekkel. koordinátatengelyt ilyen esetben az úgynevezett aszimptotákkal.
Általában bármely egyenes vonalak, amelyek korlátlanul közelebb függvény grafikonját, de nem éri el őket, nevezzük aszimptotákkal. Mi túlzás, mint egy parabola, van egy szimmetriatengelye. A hiperbola bemutatott a fenti ábrán, ez egy közvetlen y = x.
Most foglalkozik két közös ügyek túlzás. A grafikon a függvény y = k / x, ha k ≠ 0, lesz a hiperbola amelynek ágai vannak elrendezve vagy az első és a harmadik koordináta szögek, k> 0, vagy a második és a negyedik sarkokban a koordináta K<0.
Az alapvető tulajdonságait az y = k / x, k> 0
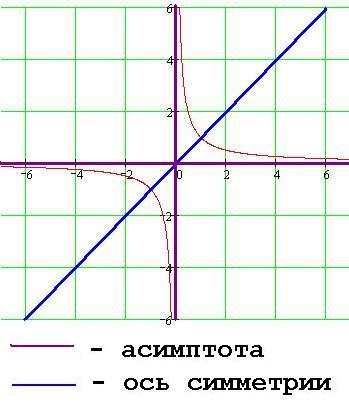
A grafikon y = k / x, k> 0
1. A pont (0, 0), a központ a szimmetria a hiperbola.
2. Tengely - asymptote túlzás.
3. Közvetlen y = x szimmetriatengelye a hiperbola.
4. a domain a funkció az összes X, kivéve X = 0.
5. y> 0 X> 0; Y6. Funkció csökken az intervallum (-∞; 0), és a (0; + ∞).
7. A funkció nem korlátozódik sem az alsó vagy a felső.
8. funkció nincs legnagyobb vagy legkisebb érték.
9. A függvény folytonos az intervallum (-∞; 0), és a (0; + ∞). Ez egy folytonossági hiány az x = 0.
10. A függvény értékei FIELD két nyitott intervallum (-∞; 0) és (0; + ∞).
Az alapvető tulajdonságait az y = k / x, k<0
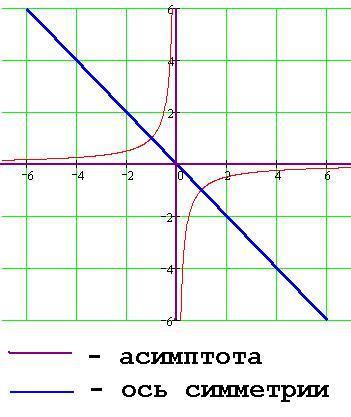
A grafikon y = k / x, k<0
1. A pont (0, 0), a központ a szimmetria a hiperbola.
2. Tengely - asymptote túlzás.
3. Közvetlen y = -x szimmetriatengelye a hiperbola.
4. a domain a funkció az összes X, kivéve X = 0.
6. A funkció növeli az intervallum (-∞; 0), és a (0; + ∞).
7. A funkció nem korlátozódik sem az alsó vagy a felső.
8. funkció nincs legnagyobb vagy legkisebb érték.
9. A függvény folytonos az intervallum (-∞; 0), és a (0; + ∞). Ez egy folytonossági hiány az x = 0.
10. A függvény értékei FIELD két nyitott intervallum (-∞; 0) és (0; + ∞).