A szög a két sík között

Legyen a sík α1 és a2 általános egyenletek. Ezután a szög φ síkok közötti α1 és α2 jelenti a legkisebb szög, ahol szükség van viszont az egyik sík előtt átfedésben van egy másik síkon. ezért

. Nyilvánvaló, hogy vagy φ = (^) Vagy φ = (-^), Aholés- normál vektorok síkok α1 és α2 rendre. Mindenesetre,

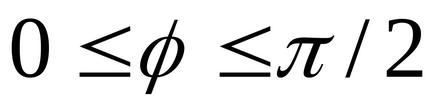
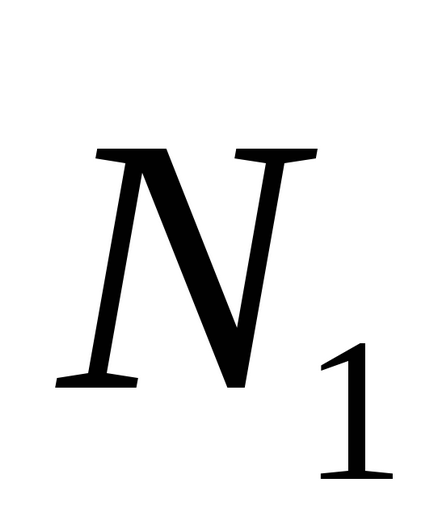
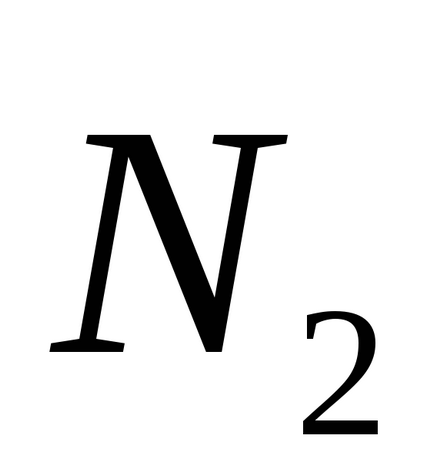
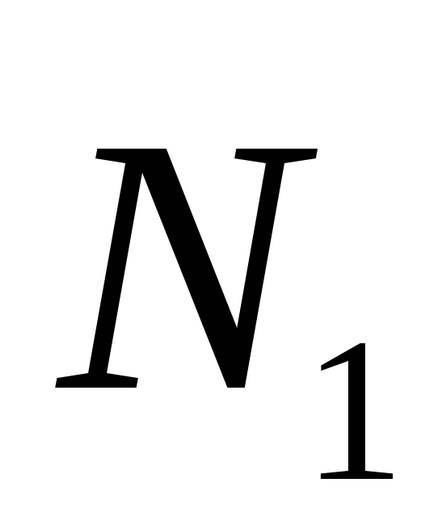
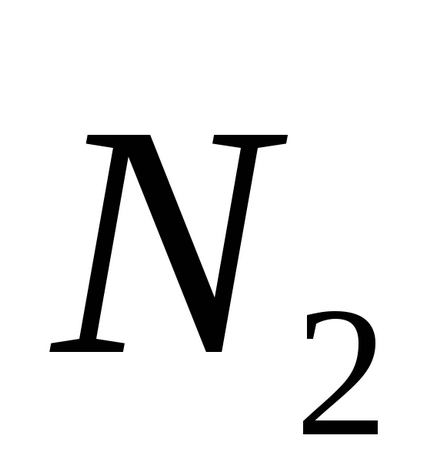
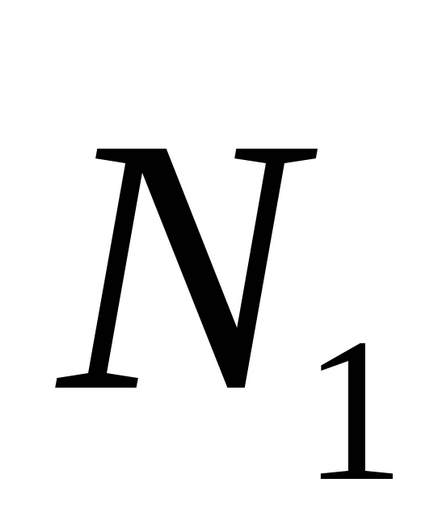
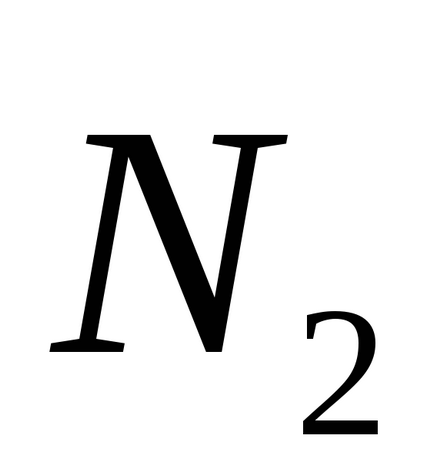
Különösen, amikor a φ = π / 2, akkor

- állapotától merőlegességének két sík.

Vonal a térben. A kölcsönös elrendezése vonal és sík a tér közvetlen egyenlet térben

Nyilvánvaló, hogy a vonal a térben lehet meghatározni, mint a kereszteződés két sík α1 és α2. Ezután egy tetszőleges affin egyenes meghatározott koordináta-rendszerben egy rendszer két lineáris egyenletek

- általános egyenlete egy egyenes vonalú vagy egy egyenlet általános formája.

Legyen l - közvetlen. Ezután pozícióját a térben egyértelműen definiált megadja annak irányvektor

= (M, n, p) és a pontot M0 (x0, y0, z0), amelyen keresztül a vonal áthalad. Vegyük bármely ponton M (x, y, z)l. majd és ezért

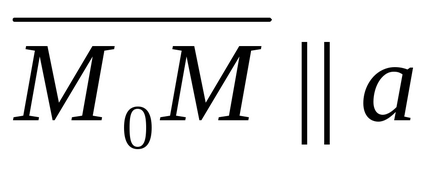
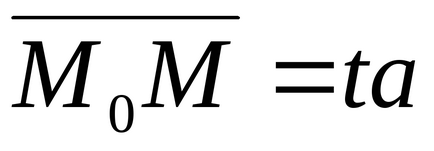
Rátérve a koordinátákat,

X - x0 = tm, y - y0 = tn, z - z0 = tp

-parametrikus egyenes egyenlete.

Kifejezése a t paraméter. megkapjuk

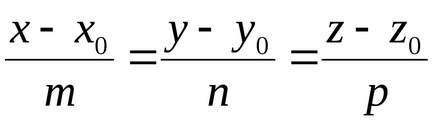
- kanonikus egyenes egyenlete ponton áthaladó

M0 (h0y0, z0) párhuzamosan a vektor

= (M, n, p).

Az utolsó egyenlet egyenértékű

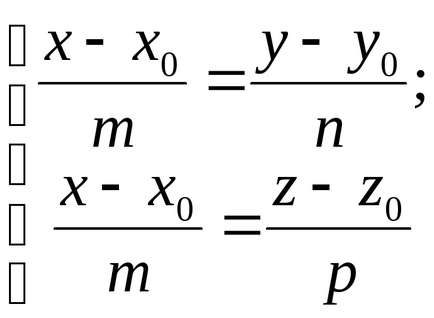
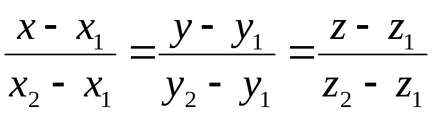
- Az egyenes egyenlete áthaladó két megadott pont.

Éppen ellenkezőleg, hagyja, hogy egy általános egyenes egyenlete.

Figyelembe tetszőleges pont M0 (x0, y0, z0) kap egyenes

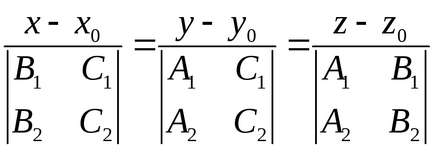
- kanonikus egyenes egyenlete.

Relatív helyzete a két egyenes vonal az űrben

Hagyja, hogy a vonalak, L1 és L2 adott kanonikus egyenletek

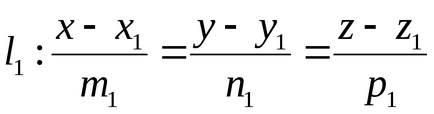
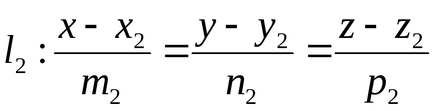
jelent

== (X2 -X1, y2 -U1, z2 -Z1), = (M1, N1, p)

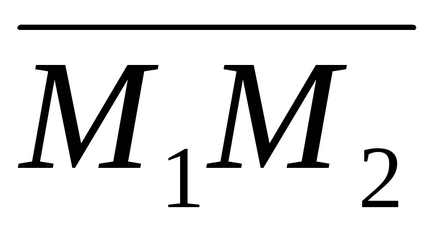
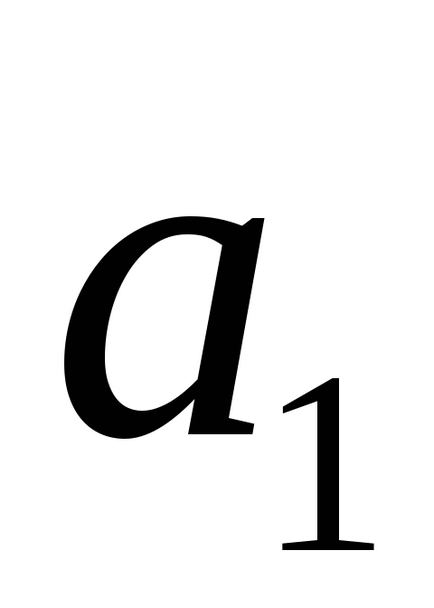
1) Ha a vonalak az azonos, mind a három vektor

,,egyenesbe esik.

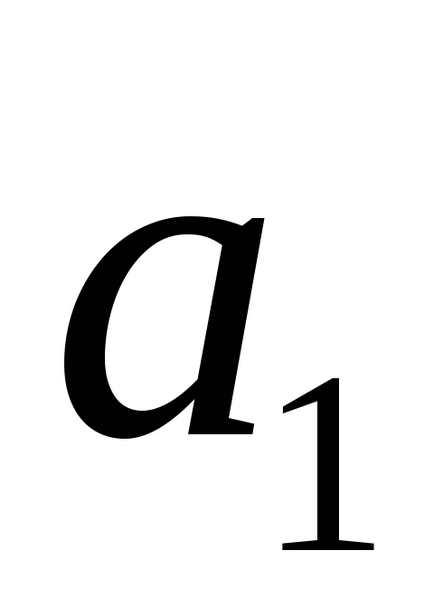
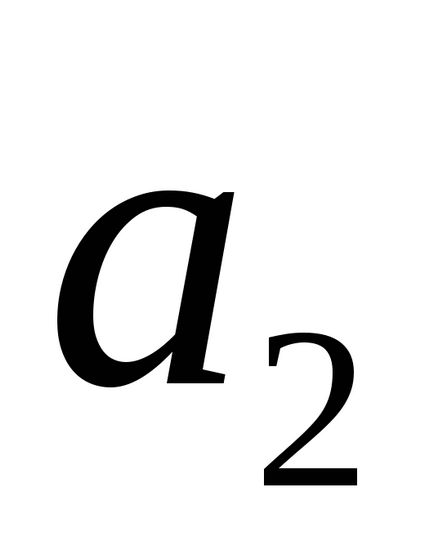
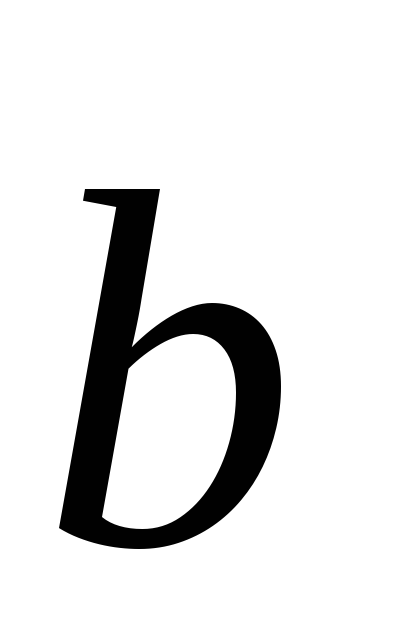
2) Ha a vonalak párhuzamosak, és nem esnek egybe, akkor a vektor

és kollineáris, és a vektorezek nem esik.

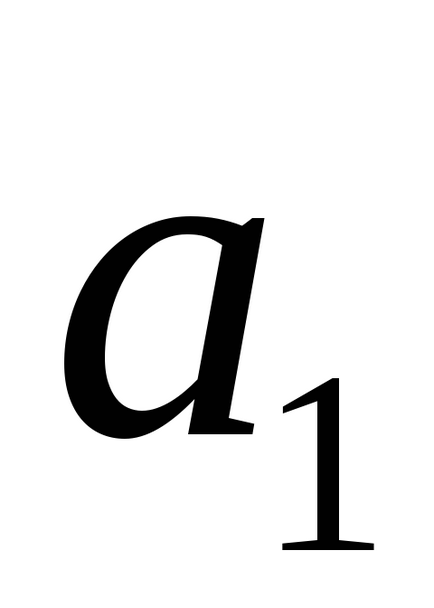
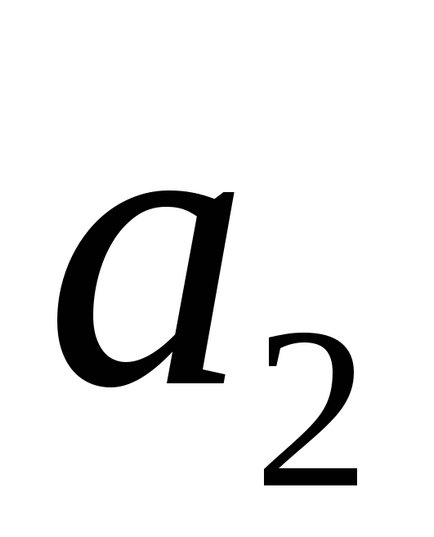
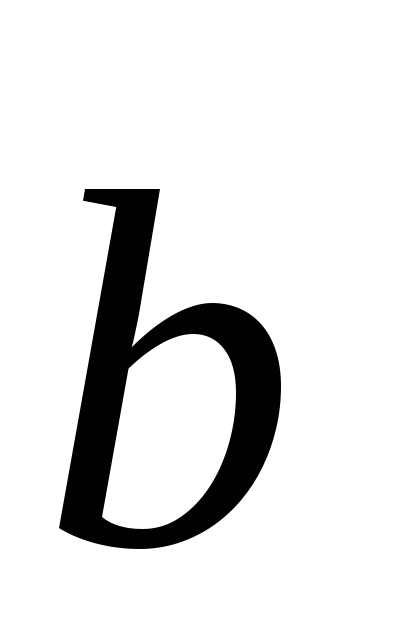
3) ha a fonalat metszik, nincs két vektorok

, ,egy egyenesbe esik, és mind a három vektor egy síkban vannak.

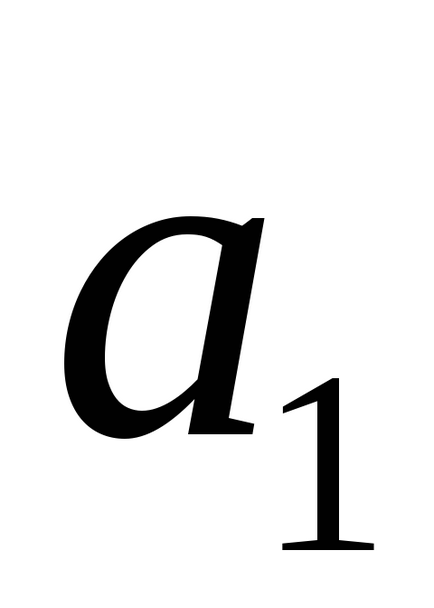
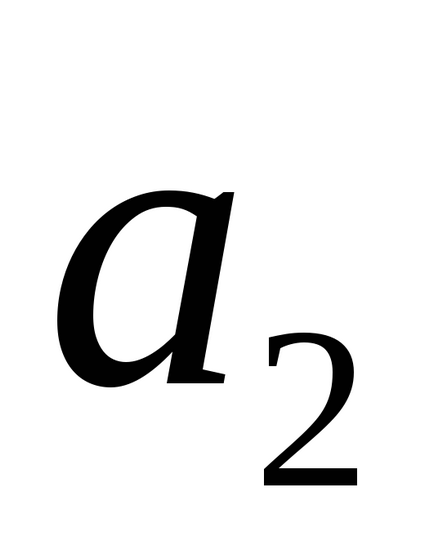
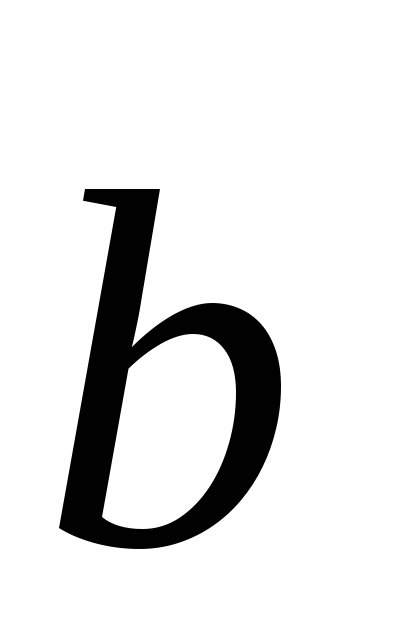
4) ha ti egyenes keresztbe, majd a vektorok

,,nem egy síkban vannak.

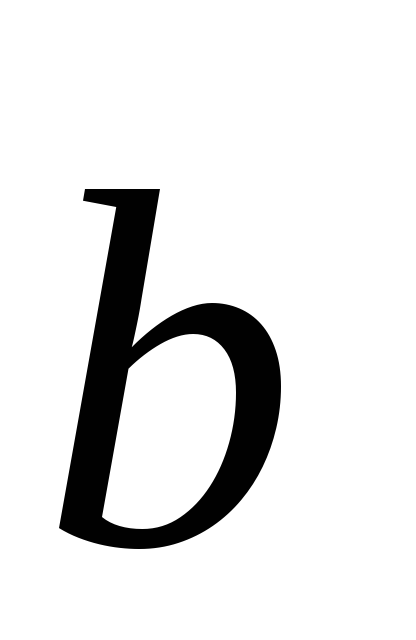
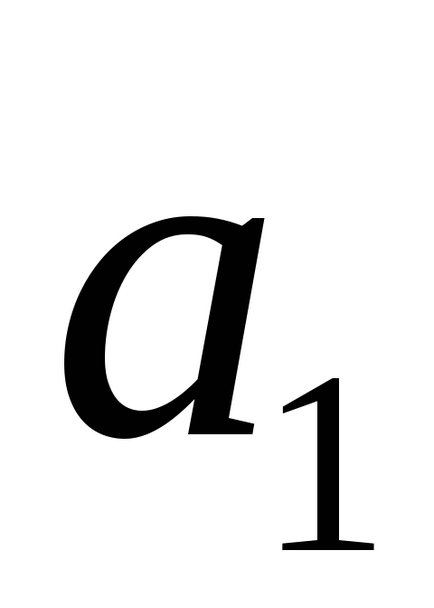
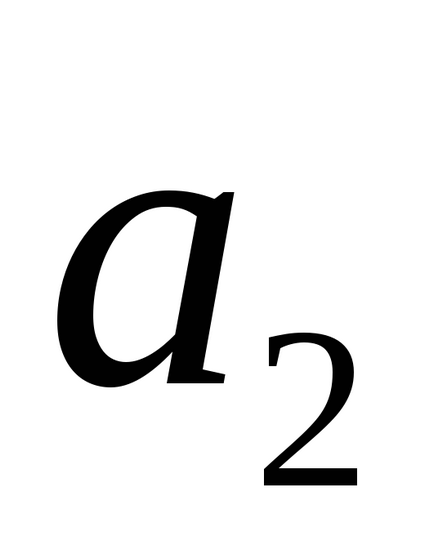
Megjegyezzük, hogy a feltételeket, a párhuzamos és merőleges, egyenes vonalak L1 és L2 jelentése egyenértékű kifejezések egy egyenesbe esik, és a merőleges irányban vektorok

és .

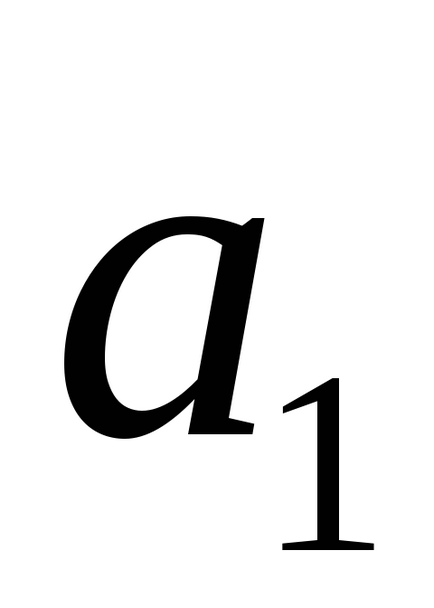
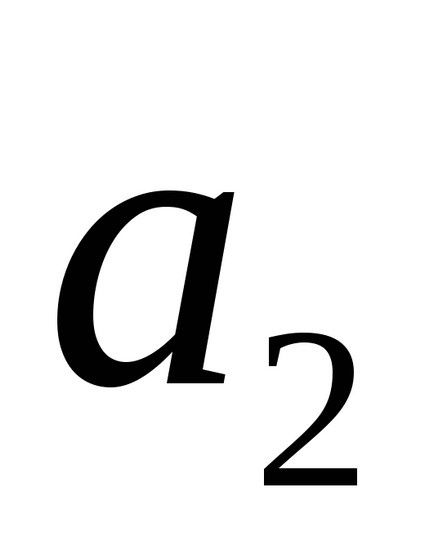
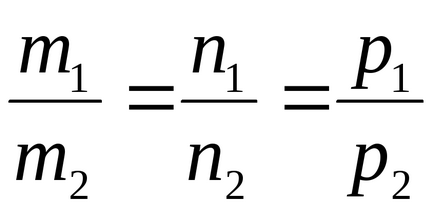
- szükséges és elégséges feltétele két párhuzamos vonal.

- szükséges és elégséges feltétele két merőleges vonalak.

Ha a vonalak L1 és L2 metszik egymást, a szög φ közöttük egyenlő vagy (

^) Vagy (-^). ezért

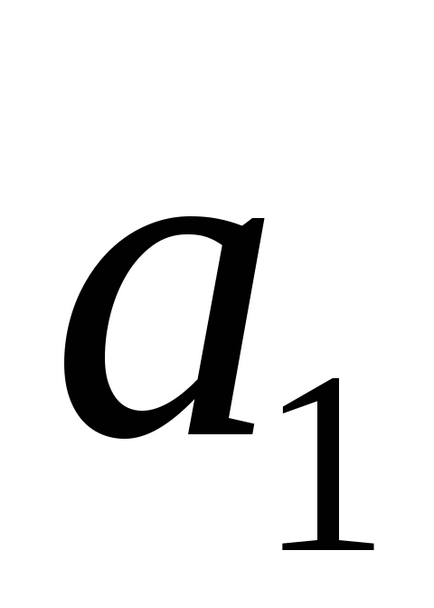
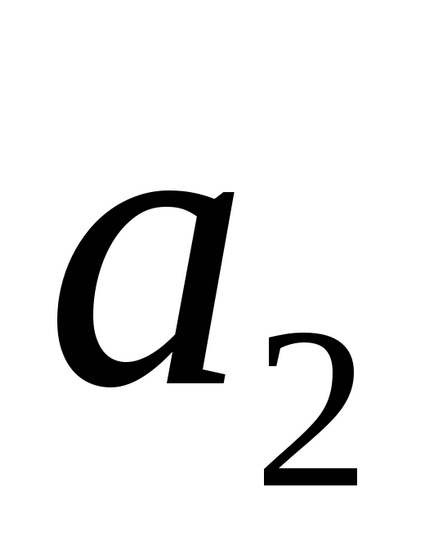
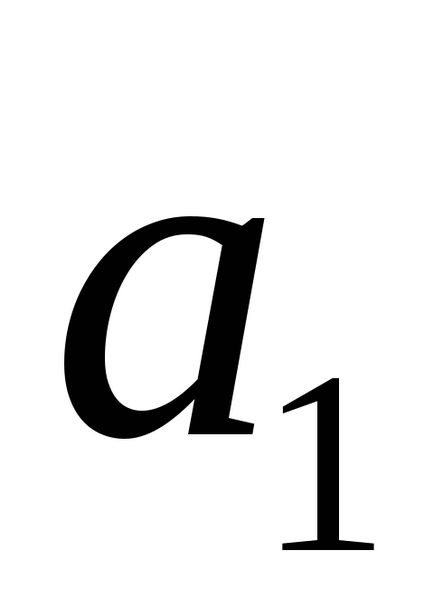
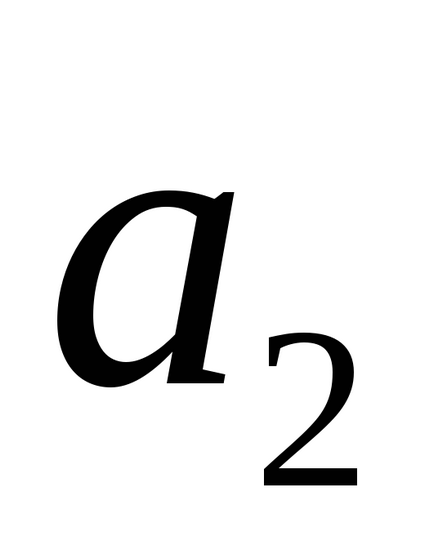
A távolság a pont a vonal az űrben

Rasstoyanied M1 ponttól (x1, y1, z1) egy adott vonal

, áthaladó tochkuM0 (x0, y0, z0) a irányvektor = (M, n, p) úgy definiáljuk, mint.

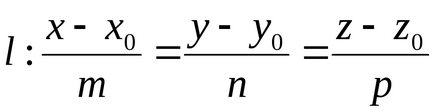
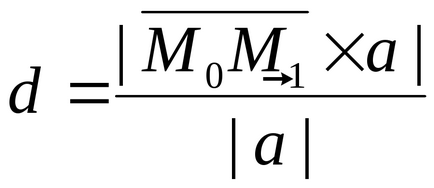
Az egyenlet a átmenő sík két adott közvetlen

Hagyja, hogy a sík α áthaladó közvetlen L1 és L2. által megadott egyenletek:

Hagyja, M2 (x2, y2, z2)

= (M1, N1, p1), = (M2, N2, P2) és M (x, y, z) síkja tetszőleges pont α

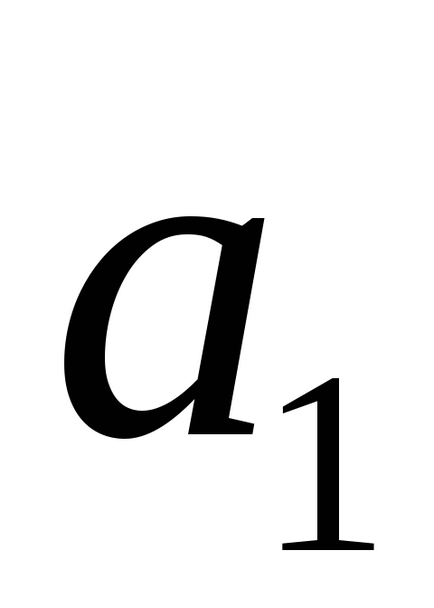
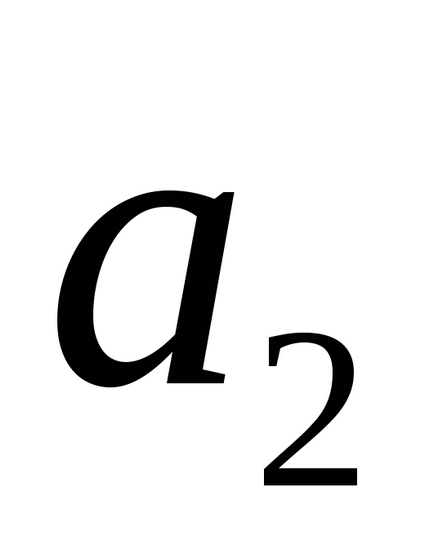
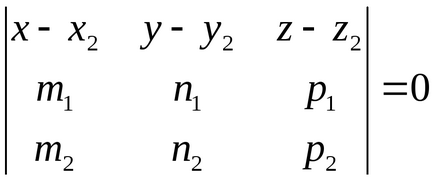
-egyenlete átmenő sík a két sor.

A távolság a kitérő egyenes

Hagyja, hogy a vonalak L1 és L2. által megadott egyenletek (2) vannak ferde. Ezután a d távolság a kettő között a hossza a merőleges levont egy sort a másik. Megjegyezzük, hogy a kívánt távolságot a szegmens a merőleges síkok injektált közötti α1 és α2. ahol α1 és α2 ugyanakkor a párhuzamos síkban vektorok

és, és kiterjesztése rendre keresztül pryamyel1 és L2

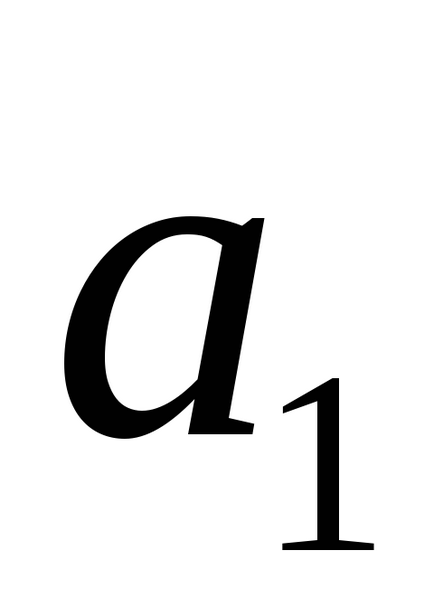
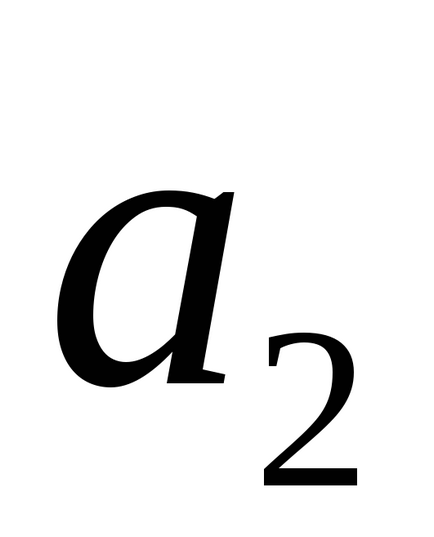
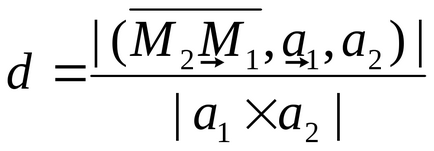
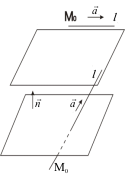
A kölcsönös elrendezése vonal és sík

Hagyja, hogy a vonal l, és a sík α leíró egyenletek

, α: ax + by + Cz + D = 0.

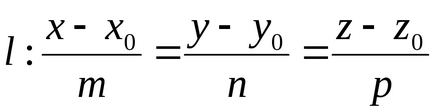
1) pryamayal síkjában fekszik α, ha

2) síkjával párhuzamosan a sor l α, ha

Kapcsolódó cikkek

• Nyomai a sík - a problémák megoldását az ellenőrzés

• Üdülőközpont holtág tó Uvildy

• Szocsi, holtág vélemények és fotók